class Solution: def LCS(self,A,B): if not A or not B: #边界处理 return 0 dp = [[0 for _ in range(len(B)+1)]for _ in range(len(A)+1)]#状态定义,dp[i][j]表示当前最长公共的长度 for i in range(1,len(A)+1): #遍历A序列 for j in range(1,len(B)+1): #遍历B序列,时间复杂度为n2 if A[i-1] == B[j-1]: #如果此时两个值相等 dp[i][j] = dp[i-1][j-1] + 1 #状态转移为前一时刻状态加1 else: #不相等的话 dp[i][j] = max(dp[i][j-1],dp[i-1][j]) #当前时刻的状态为,前两个时刻的较大值 print(B) self.printDP(dp) return dp[-1][-1] #最优解是最后的状态值 def printDP(self,dp): #打印转态 for i in range(len(dp)): for j in range(len(dp[i])): print(dp[i][j],end=' ') print() if __name__ == '__main__': solution = Solution() A = [1, 2, 3, 5, 2, 1] B = [3, 2, 1, 4, 7] res = solution.LCS(A,B) print('最长公共子序列长度为:',res)
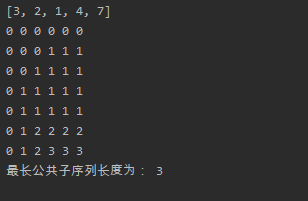
结果如下:[3,2,1]是最长的共子序列