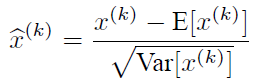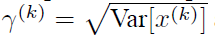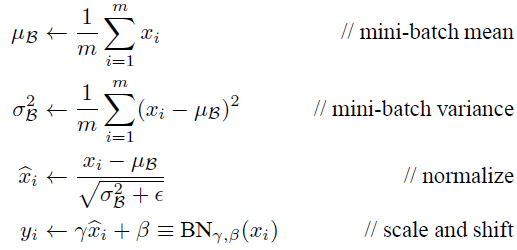Batch Nornalization
Question?
1.是什么?
2.有什么用?
3.怎么用?
paper:《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》
先来思考一个问题:我们知道在神经网络训练开始前,都要对输入数据做一个归一化处理,那么具体为什么需要归一化呢?归一化后有什么好处呢?原因在于神经网络学习过程本质就是为了学习数据分布,一旦训练数据与测试数据的分布不同,那么网络的泛化能力也大大降低;另外一方面,一旦每批训练数据的分布各不相同(batch 梯度下降),那么网络就要在每次迭代都去学习适应不同的分布,这样将会大大降低网络的训练速度,这也正是为什么我们需要对数据都要做一个归一化预处理的原因。
对于深度网络的训练是一个复杂的过程,只要网络的前面几层发生微小的改变,那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变,那么这一层网络就需要去适应学习这个新的数据分布,所以如果训练过程中,训练数据的分布一直在发生变化,那么将会影响网络的训练速度。
我们知道网络一旦train起来,那么参数就要发生更新,除了输入层的数据外(因为输入层数据,我们已经人为的为每个样本归一化),后面网络每一层的输入数据分布是一直在发生变化的,因为在训练的时候,前面层训练参数的更新将导致后面层输入数据分布的变化。以网络第二层为例:网络的第二层输入,是由第一层的参数和input计算得到的,而第一层的参数在整个训练过程中一直在变化,因此必然会引起后面每一层输入数据分布的改变。我们把网络中间层在训练过程中,数据分布的改变称之为:“Internal Covariate Shift”。Paper所提出的算法,就是要解决在训练过程中,中间层数据分布发生改变的情况,于是就有了Batch Normalization,这个牛逼算法的诞生。
1.1 BN是什么?
就像激活函数层、卷积层、全连接层、池化层一样,BN(Batch Normalization)也属于网络的一层。在前面我们提到网络除了输出层外,其它层因为低层网络在训练的时候更新了参数,而引起后面层输入数据分布的变化。这个时候我们可能就会想,如果在每一层输入的时候,再加个预处理操作那该有多好啊,比如网络第三层输入数据X3(X3表示网络第三层的输入数据)把它归一化至:均值0、方差为1,然后再输入第三层计算,这样我们就可以解决前面所提到的“Internal Covariate Shift”的问题了。
而事实上,paper的算法本质原理就是这样:在网络的每一层输入的时候,又插入了一个归一化层,也就是先做一个归一化处理,然后再进入网络的下一层。不过文献归一化层,可不像我们想象的那么简单,它是一个可学习、有参数的网络层。既然说到数据预处理,下面就先来复习一下最强的预处理方法:白化。
说到神经网络输入数据预处理,最好的算法莫过于白化预处理。然而白化计算量太大了,很不划算,还有就是白化不是处处可微的,所以在深度学习中,其实很少用到白化。经过白化预处理后,数据满足条件:a、特征之间的相关性降低,这个就相当于pca;b、数据均值、标准差归一化,也就是使得每一维特征均值为0,标准差为1。如果数据特征维数比较大,要进行PCA,也就是实现白化的第1个要求,是需要计算特征向量,计算量非常大,于是为了简化计算,作者忽略了第1个要求,仅仅使用了下面的公式进行预处理,也就是近似白化预处理:
公式简单粗糙,但是依旧很牛逼。因此后面我们也将用这个公式,对某一个层网络的输入数据做一个归一化处理。需要注意的是,我们训练过程中采用batch 随机梯度下降,上面的E(xk)指的是每一批训练数据神经元xk的平均值;然后分母就是每一批数据神经元xk激活度的一个标准差了。
1.2 BN算法实现
其实如果是仅仅使用上面的归一化公式,对网络某一层A的输出数据做归一化,然后送入网络下一层B,这样是会影响到本层网络A所学习到的特征的。打个比方,比如我网络中间某一层学习到特征数据本身就分布在S型激活函数的两侧,你强制把它给我归一化处理、标准差也限制在了1,把数据变换成分布于s函数的中间部分,这样就相当于我这一层网络所学习到的特征分布被你搞坏了,这可怎么办?于是文献使出了一招惊天地泣鬼神的招式:变换重构,引入了可学习参数γ、β,这就是算法关键之处:
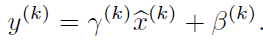
每一个神经元xk都会有一对这样的参数γ、β。这样其实当:
是可以恢复出原始的某一层所学到的特征的。因此我们引入了这个可学习重构参数γ、β,让我们的网络可以学习恢复出原始网络所要学习的特征分布。最后Batch Normalization网络层的前向传导过程公式就是:
上面的公式中m指的是mini-batch size。
源码实现:
m = K.mean(X, axis=-1, keepdims=True)#计算均值 std = K.std(X, axis=-1, keepdims=True)#计算标准差 X_normed = (X - m) / (std + self.epsilon)#归一化 out = self.gamma * X_normed + self.beta#重构变换
2.BN有什么用?
随机梯度下架成了训练深度网络的主流方法。尽管随机梯度下降法对于训练深度网络简单高效,但是它有个毛病,就是需要我们人为的去选择参数,比如学习率、参数初始化、权重衰减系数、Drop out比例等。这些参数的选择对训练结果至关重要,以至于我们很多时间都浪费在这些的调参上。那么学完这篇文献之后,你可以不需要那么刻意的慢慢调整参数。BN算法(Batch Normalization)其强大之处如下:
(1)你可以选择比较大的初始学习率,让你的训练速度飙涨。以前还需要慢慢调整学习率,甚至在网络训练到一半的时候,还需要想着学习率进一步调小的比例选择多少比较合适,现在我们可以采用初始很大的学习率,然后学习率的衰减速度也很大,因为这个算法收敛很快。当然这个算法即使你选择了较小的学习率,也比以前的收敛速度快,因为它具有快速训练收敛的特性;
(2)你再也不用去理会过拟合中drop out、L2正则项参数的选择问题,采用BN算法后,你可以移除这两项了参数,或者可以选择更小的L2正则约束参数了,因为BN具有提高网络泛化能力的特性;
(3)再也不需要使用使用局部响应归一化层了(局部响应归一化是Alexnet网络用到的方法,搞视觉的估计比较熟悉),因为BN本身就是一个归一化网络层;
(4)可以把训练数据彻底打乱(防止每批训练的时候,某一个样本都经常被挑选到)。
- 加大探索步长,加快收敛速度。
- 更容易跳出局部极小。
- 破坏原来的数据分布,一定程度上防止过拟合。
- 解决收敛速度慢和梯度爆炸。
3.在实际tensorflow框架中怎么用?
tensorflow 在实现Batch Normalization (各个网络层输出的结果归一化,以防止过拟合)时,主要用到一下两个API。分别是
3.1:tf.nn.moments
tf.nn.moments(x, axes, name=None, keep_dims=False) ⇒ mean, variance
其中计算的得到的为统计矩,mean 是一阶矩,variance 是二阶中心矩 各参数的另一为
- x 可以理解为我们输出的数据,形如 [batchsize, height, width, kernels]
- axes 表示在哪个维度上求解,是个list,例如 [0, 1, 2]
- name 就是个名字,
- keep_dims 是否保持维度
Example:
IN: img = tf.Variable(tf.random_normal([2, 3])) axis = list(range(len(img.get_shape()) - 1)) mean, variance = tf.nn.moments(img, axis) OUT: img = [[ 0.69495416 2.08983064 -1.08764684] [ 0.31431156 -0.98923939 -0.34656194]] mean = [ 0.50463283 0.55029559 -0.71710438] variance = [ 0.0362222 2.37016821 0.13730171]
3.2 tf.nn.batch_normalization
tf.nn.batch_normalization(x, mean, variance, offset, scale, variance_epsilon, name=None)
tf.nn.batch_norm_with_global_normalization(t, m, v, beta, gamma, variance_epsilon, scale_after_normalization, name=None)
由函数接口可知,tf.nn.moments 计算返回的 mean 和 variance 作为 tf.nn.batch_normalization 参数进一步调用;
def batch_norm(x, name_scope, training, epsilon=1e-3, decay=0.99): """ Assume 2d [batch, values] tensor""" with tf.variable_scope(name_scope): size = x.get_shape().as_list()[1] scale = tf.get_variable('scale', [size], initializer=tf.constant_initializer(0.1)) offset = tf.get_variable('offset', [size]) pop_mean = tf.get_variable('pop_mean', [size], initializer=tf.zeros_initializer(), trainable=False) pop_var = tf.get_variable('pop_var', [size], initializer=tf.ones_initializer(), trainable=False) batch_mean, batch_var = tf.nn.moments(x, [0]) train_mean_op = tf.assign(pop_mean, pop_mean*decay+batch_mean*(1-decay)) train_var_op = tf.assign(pop_var, pop_var*decay + batch_var*(1-decay)) def batch_statistics(): with tf.control_dependencies([train_mean_op, train_var_op]): return tf.nn.batch_normalization(x, batch_mean, batch_var, offset, scale, epsilon) def population_statistics(): return tf.nn.batch_normalization(x, pop_mean, pop_var, offset, scale, epsilon) return tf.cond(training, batch_statistics, population_statistics)