F. Ray in the tube
题意:
有两条平行于x轴的直线A,B,每条直线上的某些位置有传感器。你需要确定A,B轴上任意两个整点位置$x_a$,$x_b$,使得一条光线沿$x_a→x_b$射出(碰到A,B后反射),能够碰到的传感器数量最多是多少。 每条直线上的传感器数量≤105,0≤xi≤109
分析:
很有意思的一道题。
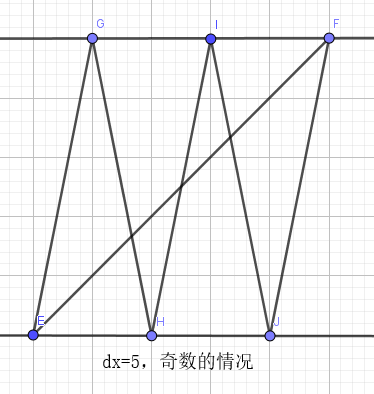
发现和y没什么关系,只要确定$x_a$,$x_b$之间的水平距离差dx就行了。
然后寻找性质:
1、如果dx为奇数,那么dx一定可以用1来代替,并且不会更差。
2、如果dx为偶数,那么dx一定可以用2的幂来代替,并且不会更差。
于是可以枚举dx,然后判断。复杂度$O(nlognlog(10^9))$

代码:
#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cmath> #include<cctype> #include<set> #include<queue> #include<vector> #include<map> using namespace std; typedef long long LL; inline int read() { int x=0,f=1;char ch=getchar();for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1; for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';return x*f; } const int N = 200005; int A[N], B[N], C[N]; int main() { int n = read();read(); for (int i = 1; i <= n; ++i) A[i] = read(); int m = read();read(); for (int i = 1; i <= m; ++i) B[i] = read(); int ans = 2; C[n + m + 1] = 1e9 + 1; for (int k = 1; k <= 1000000000; k <<= 1) { for (int i = 1; i <= n; ++i) C[i] = A[i] % (k + k); for (int i = 1; i <= m; ++i) C[i + n] = (B[i] + k) % (k + k); sort(C + 1, C + n + m + 1); for (int i = 1, pre = 1; i <= n + m; ++i) if (C[i] != C[i + 1]) ans = max(ans, i - pre + 1), pre = i + 1; } cout << ans; return 0; }