一些结论

整理一些结论。

1、关于组合数

 $C_n^m = frac{n!}{m!(n-m)!}$

$C_n^m = C_n^{m-1} + C_{n-1}^{m-1}$

$C^0_n+C^1_n+C^2_n+...+C^{n-1}_n+C^n_n=2^n$

$C_n^m ≡ C_{n/p}^{m/p} cdot C_{n\%p}^{m\%p} (mod p),p为质数$

 

2、二项式定理

$(a+b)^n = sumlimits_{i=0}^n C_n^i a^{n-i}b^i = C_n^0 a^n + C_n^1a^{n - 1}b + C_n^2a^{n - 2}b^2 + ... + C_n^{n - 1}ab^{n-1} + C_n^nb^n$

3、burnside引理和Polya定理

设$G={p_1,p_2,…,p_k}$是目标集[1,n]上的置换群。则本质不同的方案数L：

$L = frac{1}{|G|}[c(p_1)+c(p_2)+...+c(p_i)]$

$c(p_i)$表示在置换$p_i$下长度为1的循环的个数，即不动点的个数，经过此置换后不变。

设G是n个对象的一个置换群, 用m种颜色染图这n个对象，则不同的染色方案数为：

$L = frac{1}{|G|}(m^{c(p_1)}+m^{c(p_2)}+...+m^{c(p_k)})$

$c(p_i)$ 表示置换 $pi$ 的循环节数

1 2 3 4 5 6

2 3 1 5 4 6

循环节为3，(1 2 3) (4 5) (6)

3、

$2 imes sumlimits_{i=1}^{n}sumlimits_{j=i+1}^{n}a_i imes a_j = {(sumlimits_{i=1}^{n}a_i) ^2 - sumlimits_{i=1}^{n}a_i ^2}$ 

4、泰勒公式

5、求导公式

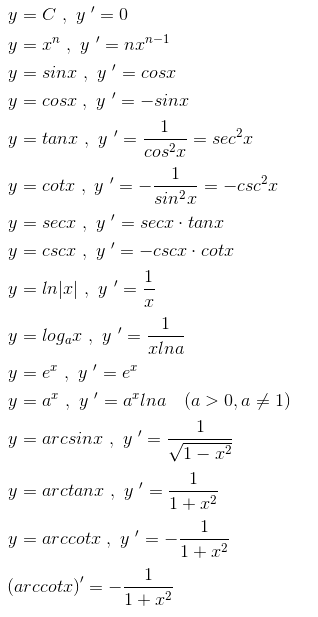
复合函数求导法则：

$h(x) = f(g(x))$

$h'(x)=f'(g(x)) imes g'(x)$

对外函数求导，对内函数求导，两者相乘。

6、常用生成函数

$frac{1}{1-x} = 1 + x + x ^ 2 + x ^ 3 + cdots$

$frac{a}{1-x} = a + ax + x ^ 2 + ax ^ 3 + cdots$

$frac{1}{1-x^2} = 1 + x^2 + x ^ 4 + x ^ 6 + cdots$

$frac{1}{(1-x)^2} = 1 + 2x +3 x ^ 2 +4 x ^ 3 + cdots$

7、两点之间的次短路

求S出发的最短路和从T出发的最短路，枚举每条边，次短路一定在dis1[u]+w+dis[v]中。

8、等差数列求和公式

设首项为$a_1$ , 末项为$a_n$, 项数为$n$ , 公差为$d$ , 前$n$项和为$S_n$ , 则有:

$a_n = a_1 + (n - 1)$

$S_n = n imes a_1 + frac{n imes (n - 1) imes d}{2}$

$S_n = frac{(a_1 + a_n) imes n}{2}$

8、等比序列求和公式

公式中$a_1$为首项，$a_n$为数列第n项，$q$为等比数列公比，$S_n$为前n项和。

$a_n = a_1 imes q^{n - 1}$

$S_n = n imes a_1 (q = 1)$

$S_n = a_1 imes frac{1 - q^n}{1 - q} = frac{a_1 - a_n imes q}{1 - q} (q eq 1 )$

9、莫队的神奇排序方法

bool operator < (const Que &A,const Que &B) {
      return bel[A.l] < bel[B.l] || (bel[A.l] == bel[B.l] && ((bel[A.l] & 1) ? A.r < B.r : A.r > B.r));
}

---------------