04/17
目前做了:7题
由于目前六道都是1A感觉非常爽...
BZOJ1412: [ZJOI2009]狼和羊的故事
“狼爱上羊啊爱的疯狂,谁让他们真爱了一场;狼爱上羊啊并不荒唐,他们说有爱就有方向......” Orez听到这首歌,心想:狼和羊如此和谐,为什么不尝试羊狼合养呢?说干就干! Orez的羊狼圈可以看作一个n*m个矩阵格子,这个矩阵的边缘已经装上了篱笆。可是Drake很快发现狼再怎么也是狼,它们总是对羊垂涎三尺,那首歌只不过是一个动人的传说而已。所以Orez决定在羊狼圈中再加入一些篱笆,还是要将羊狼分开来养。 通过仔细观察,Orez发现狼和羊都有属于自己领地,若狼和羊们不能呆在自己的领地,那它们就会变得非常暴躁,不利于他们的成长。 Orez想要添加篱笆的尽可能的短。当然这个篱笆首先得保证不能改变狼羊的所属领地,再就是篱笆必须修筑完整,也就是说必须修建在单位格子的边界上并且不能只修建一部分。
首先这道题的题意很显然,就是让我们用最少的篱笆数分开狼群和羊群
再简化,也就是用最少的边切断所有狼和羊的联系,这么一来就是最小割问题了
建立一个源点连接所有的狼,所有的羊再向汇点各连一条边,这些边的容量都设为正无穷,表示不能切开
对于相邻的格子建立容量为1的边,同一种群之间不能建边,羊不需要建出边
然后跑最大流就可以了
BZOJ2424: [HAOI2010]订货
某公司估计市场在第i个月对某产品的需求量为Ui,已知在第i月该产品的订货单价为di,上个月月底未销完的单位产品要付存贮费用m,假定第一月月初的库存量为零,第n月月底的库存量也为零,问如何安排这n个月订购计划,才能使成本最低?每月月初订购,订购后产品立即到货,进库并供应市场,于当月被售掉则不必付存贮费。假设仓库容量为S。
和餐巾计划问题几乎一模一样,需要改变的两点
一个是从源点连向左边的点的费用不再为0,而是为当天购买的费用
因为这道题并不能重复利用只能提前购买
第二个就是仓库有容量(刚开始多想了认为当天用掉的商品也要计算在库存内
这个只需要拆点就可以了
最小费用最大流
BZOJ1934: [Shoi2007]Vote 善意的投票
幼儿园里有n个小朋友打算通过投票来决定睡不睡午觉。对他们来说,这个问题并不是很重要,于是他们决定发扬谦让精神。虽然每个人都有自己的主见,但是为了照顾一下自己朋友的想法,他们也可以投和自己本来意愿相反的票。我们定义一次投票的冲突数为好朋友之间发生冲突的总数加上和所有和自己本来意愿发生冲突的人数。 我们的问题就是,每位小朋友应该怎样投票,才能使冲突数最小?
建立一个源点,连接所有意愿为0的小朋友,建立汇点连接意愿为1的小朋友,边容量均为1
在好朋友之间建立一条容量为1的边
然后这道题让我们求的最小冲突数就是最小割了
最大流跑一遍即可
BZOJ3171: [Tjoi2013]循环格
一个循环格就是一个矩阵,其中所有元素为箭头,指向相邻四个格子。每个元素有一个坐标(行,列),其中左上角元素坐标为(0,0)。给定一个起始位置(r,c)
,你可以沿着箭头防线在格子间行走。即如果(r,c)是一个左箭头,那么走到(r,c-1);如果是右箭头那么走到(r,c+1);如果是上箭头那么走到(r-1,c);如果是下箭头那么走到(r+1,c);每一行和每一列都是循环的,即如果走出边界,你会出现在另一侧。
一个完美的循环格是这样定义的:对于任意一个起始位置,你都可以i沿着箭头最终回到起始位置。如果一个循环格不满足完美,你可以随意修改任意一个元素的箭头直到完美。给定一个循环格,你需要计算最少需要修改多少个元素使其完美。
这道题的突破口在于挖掘完美循环格的性质:每个格子的入度都为1!(出度自然为1)
然后做法就和混合图的欧拉回路判定一样了
源点连接入度<1的点,容量为1-b[i],汇点连接入度>1的点,容量为b[i]-1
对于一个箭头我们将它可以转向的点向它原来的点连一条容量为1费用为1的边
最小费用最大流求解
BZOJ1433: [ZJOI2009]假期的宿舍
题意很明显,只需要将每个人和每个人的床看做二分图,然后跑最大流就可以了
每个在校的学生的床可以用,床与t连一条容量为1的边
每个外校来的或者在校的不回去的学生要睡,s与学生连一条容量为1的边
然后每个人和认识的人的床连一条边
自己和自己的床连一条边即可
BZOJ2132: 圈地计划
最近房地产商GDOI(Group of Dumbbells Or Idiots)从NOI(Nuts Old Idiots)手中得到了一块开发土地。据了解,这块土地是一块矩形的区域,可以纵横划分为N×M块小区域。GDOI要求将这些区域分为商业区和工业区来开发。根据不同的地形环境,每块小区域建造商业区和工业区能取得不同的经济价值。更具体点,对于第i行第j列的区域,建造商业区将得到Aij收益,建造工业区将得到Bij收益。另外不同的区域连在一起可以得到额外的收益,即如果区域(I,j)相邻(相邻是指两个格子有公共边)有K块(显然K不超过4)类型不同于(I,j)的区域,则这块区域能增加k×Cij收益。经过Tiger.S教授的勘察,收益矩阵A,B,C都已经知道了。你能帮GDOI求出一个收益最大的方案么?
这道题与以前做的最小割题目相比有所不同
因为我们可以很显然地将点与s,t连边的想法想出来
但是类型不同的区域能获得收益这一点导致不知道应该怎么连边..
割开了反而能获得收益?容量为负?什么啊...
解法很巧妙,由于矩形中的格子根据其横纵坐标的奇偶性可以分为两类格子
每一类与另一类的格子之间才有连边
所以我们可以分两类考虑,对于一类格子,s代表工业区,t代表商业区
对于另一类格子,s代表商业区,t代表工业区
此时只有在同一侧的格子才能获得收益了,于是转化成了我们熟悉的最小割
再次运用到了源点汇点不止单一含义的思想
好好体会
2127: happiness
高一一班的座位表是个n*m的矩阵,经过一个学期的相处,每个同学和前后左右相邻的同学互相成为了好朋友。这学期要分文理科了,每个同学对于选择文科与理科有着自己的喜悦值,而一对好朋友如果能同时选文科或者理科,那么他们又将收获一些喜悦值。作为计算机竞赛教练的scp大老板,想知道如何分配可以使得全班的喜悦值总和最大。
这道题不管是建图还是实现都比较有学习的价值
首先刚开始我打算奇偶矩阵建图,就像上次的男生女生跳舞一样,但是发现流量无法控制
然后又重新回归到s,t分别代表文理科的思路
最后的方法非常巧妙,其实我认为比较难想到...我们发现对于任意两个相邻的点有如下性质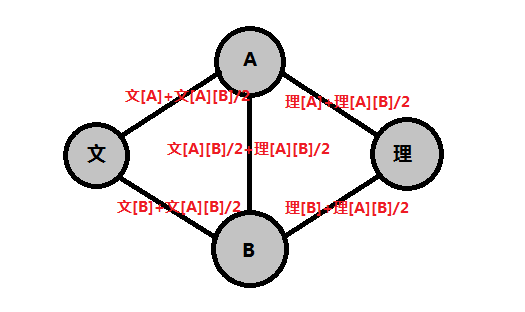
当A和B分到不同的科目的时候,首先它们中间的边肯定割掉,
其次他们肯定一个割掉文科的边一个割掉理科的边
所以正好割掉了文[A][B]+理[A][B]
当A和B分到相同科目的时候,要不割掉文[A][B]要不割掉理[A][B]
正好满足我们题目的需要!!!
然后就可以建图然后跑最大流了
但是我们发现这道题的点有点多,边也很多,按照以前的方法会TIE
有个小小的优化过程,就是对于两人之间我们平时会建两次单向边
其实将它们互作为反向弧不是就可以吗?节省了约一半的边数
