抱着好奇心态去开始做APIO的往年试题感受一下难度
Oil
Description
采油区域 Siruseri政府决定将石油资源丰富的Navalur省的土地拍卖给私人承包商以建立油井。被拍卖的整块土地为一个矩形区域,被划分为M×N个小块。 Siruseri地质调查局有关于Navalur土地石油储量的估测数据。这些数据表示为M×N个非负整数,即对每一小块土地石油储量的估计值。 为了避免出现垄断,政府规定每一个承包商只能承包一个由K×K块相连的土地构成的正方形区域。 AoE石油联合公司由三个承包商组成,他们想选择三块互不相交的K×K的区域使得总的收益最大。 例如,假设石油储量的估计值如下: 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 8 8 8 8 8 1 1 1 1 8 8 8 8 8 1 1 1 1 8 8 8 8 8 1 1 1 1 1 1 1 8 8 8 1 1 1 1 1 1 1 1 8 8 8 1 1 1 1 1 1 9 9 9 1 1 1 1 1 1 9 9 9 如果K = 2, AoE公司可以承包的区域的石油储量总和为100, 如果K = 3, AoE公司可以承包的区域的石油储量总和为208。 AoE公司雇佣你来写一个程序,帮助计算出他们可以承包的区域的石油储量之和的最大值。
首先由于是一个个正方形,所以很容易看出最终每块油田所在的区域是通过一些水平或竖直的线隔开的
并且这些线在它所在的区域内是到达边界的 这道题三个油田也就是最终只可能为下面六种情况
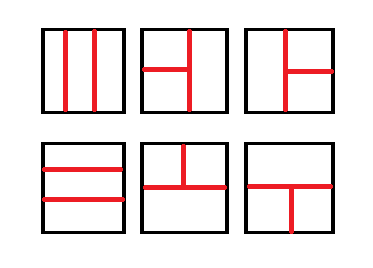
其中右边的两列看起来比较好处理
我们只要先预处理左上左下右上右下四个方向最大答案的前缀和
然后再枚举水平和竖直线的位置
稍加处理就可以得出答案
左边的一列以两条水平线为例
我们枚举一条水平线之后,枚举另一条在它下面的水平线
这条水平线每向下移一行,中间部分也就多了一行
所以我们可以预处理出每行每列的最大答案
在枚举第二条线的时候维护中间部分答案的最大值
上下部分用前缀和来计算
在写代码的过程中,由于我统计的是以(x,y)为左上角的边长为k的矩形的答案
所以前缀和部分用到的时候需要注意哪些地方需要-k+1,哪些地方是限制住的
时间复杂度O(nm)
1 /************************************************************** 2 Problem: 1177 3 User: mjy0724 4 Language: C++ 5 Result: Accepted 6 Time:6128 ms 7 Memory:54256 kb 8 ****************************************************************/ 9 10 #include<cstdio> 11 #include<cstdlib> 12 #include<cstring> 13 const int maxn = 1510; 14 int a[maxn][maxn],map[maxn][maxn],lu[maxn][maxn],ru[maxn][maxn],ld[maxn][maxn],rd[maxn][maxn],h[maxn],v[maxn]; 15 int max(int a,int b){if (a>b) return a;else return b;} 16 int main(){ 17 int n,m,k,ans=0; 18 scanf("%d%d%d",&n,&m,&k); 19 for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) scanf("%d",&map[i][j]); 20 for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) map[i][j]+=map[i-1][j]; 21 for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) map[i][j]+=map[i][j-1]; 22 for (int i=1;i<=n-k+1;i++) for (int j=1;j<=m-k+1;j++) a[i][j]=map[i+k-1][j+k-1]-map[i-1][j+k-1]-map[i+k-1][j-1]+map[i-1][j-1]; 23 for (int i=1;i<=n-k+1;i++) for (int j=1;j<=m-k+1;j++) lu[i][j]=max(max(lu[i-1][j],lu[i][j-1]),a[i][j]); 24 for (int i=1;i<=n-k+1;i++) for (int j=m-k+1;j>0;j--) ru[i][j]=max(max(ru[i-1][j],ru[i][j+1]),a[i][j]); 25 for (int i=n-k+1;i>0;i--) for (int j=1;j<=m-k+1;j++) ld[i][j]=max(max(ld[i+1][j],ld[i][j-1]),a[i][j]); 26 for (int i=n-k+1;i>0;i--) for (int j=m-k+1;j>0;j--) rd[i][j]=max(max(rd[i+1][j],rd[i][j+1]),a[i][j]); 27 for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) h[i]=max(h[i],a[i][j]),v[j]=max(v[j],a[i][j]); 28 for (int i=k;i<=n-2*k;i++){ 29 int mx = 0; 30 for (int j=i+k;j<=n-k;j++){ 31 mx = max(mx,h[j-k+1]); 32 ans = max(ans,lu[i-k+1][m-k+1]+mx+ld[j+1][m-k+1]); 33 } 34 } 35 for (int i=k;i<=n-k;i++) 36 for (int j=k;j<=m-k;j++) ans=max(ans,lu[i-k+1][j-k+1]+ru[i-k+1][j+1]+ld[i+1][m-k+1]); 37 for (int i=k;i<=n-k;i++) 38 for (int j=k;j<=m-k;j++) ans=max(ans,lu[i-k+1][m-k+1]+ld[i+1][j-k+1]+rd[i+1][j+1]); 39 40 for (int i=k;i<=m-2*k;i++){ 41 int mx=0; 42 for (int j=i+k;j<=m-k;j++){ 43 mx = max(mx,v[j-k+1]); 44 ans = max(ans,lu[n-k+1][i-k+1]+mx+ru[n-k+1][j+1]); 45 } 46 } 47 for (int i=k;i<=n-k;i++) 48 for (int j=k;j<=m-k;j++) ans=max(ans,lu[i-k+1][j-k+1]+ru[n-k+1][j+1]+ld[i+1][j-k+1]); 49 for (int i=k;i<=n-k;i++) 50 for (int j=k;j<=m-k;j++) ans=max(ans,lu[n-k+1][j-k+1]+ru[i-k+1][j+1]+rd[i+1][j+1]); 51 printf("%d ",ans); 52 return 0; 53 }
[BZOJ1178]CONVENTION会议中心
Description
Siruseri政府建造了一座新的会议中心。许多公司对租借会议中心的会堂很感兴趣,他们希望能够在里面举行会议。 对于一个客户而言,仅当在开会时能够独自占用整个会堂,他才会租借会堂。会议中心的销售主管认为:最好的策略应该是将会堂租借给尽可能多的客户。显然,有可能存在不止一种满足要求的策略。 例如下面的例子。总共有4个公司。他们对租借会堂发出了请求,并提出了他们所需占用会堂的起止日期(如下表所示)。 开始日期 结束日期 公司1 4 9 公司2 9 11 公司3 13 19 公司4 10 17 上例中,最多将会堂租借给两家公司。租借策略分别是租给公司1和公司3,或是公司2和公司3,也可以是公司1和公司4。注意会议中心一天最多租借给一个公司,所以公司1和公司2不能同时租借会议中心,因为他们在第九天重合了。 销售主管为了公平起见,决定按照如下的程序来确定选择何种租借策略:首先,将租借给客户数量最多的策略作为候选,将所有的公司按照他们发出请求的顺序编号。对于候选策略,将策略中的每家公司的编号按升序排列。最后,选出其中字典序最小1的候选策略作为最终的策略。 例中,会堂最终将被租借给公司1和公司3:3个候选策略是{(1,3),(2,3),(1,4)}。而在字典序中(1,3)<(1,4)<(2,3)。 你的任务是帮助销售主管确定应该将会堂租借给哪些公司。
这道题我觉得非常有意思,用一些简单的算法拼凑出了一个很好的解题思路,虽然代码复杂度略高
首先第一问的答案很显然...直接贪心就可以出解
我们可以考虑两段时间区间,如果其中一段包含另一段,那么显然这条长的线段是没有用的
因为在每条线段对答案的贡献都=1的情况下,选这条短的能为其他线段的摆放留有更多空间
我们把所有的这种不优秀的线段都删除掉以后,将它们按左端点从小到大排序之后
会发现右端点也是升序,因为否则就会出现包含的情况
可以考虑取了某条线段i以后,实际上下一条取哪条线段已经确定了
因为在可以取的范围(左端点大于线段i的右端点)的线段集合中,我们肯定取那个右端点最小的
由于我们上面得出左端点与右端点同时上升,二分找出第一个左端点大于线段i右端点的线段就是下一条要取的线段
这样一来好像忽然明白了:其实只要确定了起点,整个要取的线段序列都是确定的
我们可以用倍增来储存第i条线段接下去要取的第2^j条线段
直接按照题目的要求来,从小到大去试
只要当前线段能够放下(即在此之前的线段没有覆盖到这条线段所在的位置)
咦那为什么不能让之前的移一下呢?我们的顺序是从小到大,人家的优先级比你要高
所以这样做有一个比较好的性质:确定了的就不能修改
另外,还要保证放下了之后最优解不变,我们设当前线段所在的空白位置向左右延伸到的最远处分别是lx,rx,当前线段(l,r)
那么ans(lx,rx)=ans(l,lx-1)+ans(r+1,rx)+1才能够保证最优解不变
那么获取答案的函数ans如何求得呢?
上上段我们处理好了倍增的数组,ans即求一个给定起点和终点的线段区间的答案
直接用倍增处理就可以了
1 /************************************************************** 2 Problem: 1178 3 User: mjy0724 4 Language: C++ 5 Result: Accepted 6 Time:5804 ms 7 Memory:85588 kb 8 ****************************************************************/ 9 10 #include<cstdio> 11 #include<cstdlib> 12 #include<cstring> 13 #include<cmath> 14 const int maxn=400010,INF=1000000007; 15 struct point{ 16 int x,y; 17 }a[maxn],c[maxn],p[maxn]; 18 struct tree{ 19 int l,r,lx,rx,cov; 20 }tr[maxn*5]; 21 int n,tot,fa[maxn][20],ans,as[maxn],d[maxn],e[maxn]; 22 bool vis[maxn]; 23 char s[100]; 24 int max(int a,int b){ 25 if (a>b) return a; 26 else return b; 27 } 28 29 int min(int a,int b){ 30 if (a<b) return a; 31 else return b; 32 } 33 34 void sortf(int l,int r){ 35 int i=l,j=r,mid=(l+r) >> 1,midx=a[mid].x,midy=a[mid].y; 36 do{ 37 while (i<r&&((a[i].x>midx)||(a[i].x==midx&&a[i].y<midy))) i++; 38 while (l<j&&((a[j].x<midx)||(a[j].x==midx&&a[j].y>midy))) j--; 39 if (i<=j){ 40 a[0]=a[i];a[i]=a[j];a[j]=a[0]; 41 i++;j--; 42 } 43 }while (i<=j); 44 if (i<r) sortf(i,r); 45 if (l<j) sortf(l,j); 46 } 47 48 void sortg(int l,int r){ 49 int i=l,j=r,mid=p[(l+r) >> 1].x; 50 do{ 51 while (i<r&&p[i].x<mid) i++; 52 while (l<j&&p[j].x>mid) j--; 53 if (i<=j){ 54 p[0]=p[i];p[i]=p[j];p[j]=p[0]; 55 i++;j--; 56 } 57 }while (i<=j); 58 if (i<r) sortg(i,r); 59 if (l<j) sortg(l,j); 60 } 61 62 int find(int x){ 63 int ans=0,l=1,r=tot; 64 while (l<=r){ 65 int mid=(l+r) >> 1; 66 if (p[mid].x>=x){ 67 ans=mid;r=mid-1; 68 }else l=mid+1; 69 } 70 return ans; 71 } 72 void solve(){ 73 int minr=INF; 74 memset(vis,true,sizeof(vis)); 75 int j; 76 for (int i=1;i<=n;i=j){ 77 for (j=i;a[i].x==a[j].x&&j<=n;j++){ 78 if (minr<a[j].y) vis[j]=false; 79 if (a[j].y<minr) minr=a[j].y; 80 } 81 } 82 tot=0; 83 for (int i=1;i<=n;i++) if (vis[i]) p[++tot]=a[i]; 84 sortg(1,tot); 85 for (int i=1;i<=tot;i++) fa[i][0]=find(p[i].y+1); 86 for (int j=1;(1 << j)<=n;j++) 87 for (int i=1;i<=tot;i++) fa[i][j]=fa[fa[i][j-1]][j-1]; 88 } 89 90 void build(int p,int l,int r){ 91 tr[p].l=l;tr[p].r=r;tr[p].lx=INF;tr[p].rx=-INF;tr[p].cov=0; 92 if (l!=r){ 93 int mid = (l+r) >> 1; 94 build(p<<1,l,mid);build((p<<1)+1,mid+1,r); 95 } 96 } 97 98 void sorth(int l,int r){ 99 int i=l,j=r,mid=d[(l+r) >> 1]; 100 do{ 101 while (i<r&&d[i]<mid) i++; 102 while (l<j&&d[j]>mid) j--; 103 if (i<=j){ 104 int tem=d[i];d[i]=d[j];d[j]=tem; 105 i++;j--; 106 } 107 }while (i<=j); 108 if (i<r) sorth(i,r); 109 if (l<j) sorth(l,j); 110 } 111 112 void ls(){ 113 for (int i=1;i<=n;i++){ 114 d[++d[0]]=a[i].x;d[++d[0]]=a[i].y; 115 } 116 sorth(1,d[0]); 117 int j; 118 for (int i=1;i<=d[0];i=j){ 119 e[++e[0]]=d[i];j=i+1; 120 while (j<=d[0]&&d[i]==d[j]) j++; 121 } 122 } 123 124 void insert(int p,int l,int r){ 125 if (tr[p].cov) {tr[p].lx=tr[p].l,tr[p].rx=tr[p].r;} 126 if (tr[p].l==l&&tr[p].r==r){ 127 tr[p].cov=1;tr[p].lx=tr[p].l;tr[p].rx=tr[p].r; 128 return; 129 } 130 int mid = (tr[p].l+tr[p].r) >> 1; 131 if (tr[p].cov) tr[p<<1].cov=1,tr[(p<<1)+1].cov=1; 132 if (r<=mid) insert(p<<1,l,r);else 133 if (l>mid) insert((p<<1)+1,l,r);else{ 134 insert(p<<1,l,mid);insert((p<<1)+1,mid+1,r); 135 } 136 tr[p].lx=min(tr[p<<1].lx,tr[(p<<1)+1].lx); 137 tr[p].rx=max(tr[p<<1].rx,tr[(p<<1)+1].rx); 138 } 139 140 int getnum(int x){ 141 int l=1,r=e[0]; 142 while (l<=r){ 143 int mid=(l+r) >> 1; 144 if (e[mid]==x) return mid; 145 if (x<e[mid]) r=mid-1;else l=mid+1; 146 } 147 } 148 149 int getl(int p,int l,int r){ 150 if (tr[p].cov){tr[p].lx=l;tr[p].rx=r;} 151 if (tr[p].l==l&&tr[p].r==r) return tr[p].lx; 152 int mid=(tr[p].l+tr[p].r) >> 1; 153 if (tr[p].cov) tr[p<<1].cov=1,tr[(p<<1)+1].cov=1; 154 if (r<=mid) return getl(p<<1,l,r);else 155 if (l>mid) return getl((p<<1)+1,l,r); else 156 return min(getl(p<<1,l,mid),getl((p<<1)+1,mid+1,r)); 157 } 158 159 int getr(int p,int l,int r){ 160 if (tr[p].cov){tr[p].lx=l;tr[p].rx=r;} 161 if (tr[p].l==l&&tr[p].r==r) return tr[p].rx; 162 int mid=(tr[p].l+tr[p].r)>>1; 163 if (tr[p].cov) tr[p<<1].cov=1,tr[(p<<1)+1].cov=1; 164 if (r<=mid) return getr(p<<1,l,r);else 165 if (l>mid) return getr((p<<1)+1,l,r);else 166 return max(getr(p<<1,l,mid),getr((p<<1)+1,mid+1,r)); 167 } 168 169 int query(int x,int y){ 170 if (x<1||y<1||x>e[0]||y>e[0]) return 0; 171 int s=-1,l=1,r=tot; 172 while (l<=r){ 173 int mid=(l+r) >> 1; 174 if (p[mid].x>=e[x]) s=mid,r=mid-1;else l=mid+1; 175 } 176 int t=-1; 177 l=1;r=tot; 178 while (l<=r){ 179 int mid=(l+r) >> 1; 180 if (p[mid].y<=e[y]) t=mid,l=mid+1;else r=mid-1; 181 } 182 if (s==-1||t==-1||s>t) return 0; 183 int ans=1,i=log(tot)/log(2); 184 while (s<t&&i>=0){ 185 while (s<t&&fa[s][i]!=0&&fa[s][i]<=t) s=fa[s][i],ans+=1<<i; 186 i--; 187 } 188 return ans; 189 } 190 191 int main(){ 192 scanf("%d",&n); 193 for (int i=1;i<=n;i++) scanf("%d%d",&a[i].x,&a[i].y),gets(s); 194 for (int i=1;i<=n;i++) c[i].x=a[i].x,c[i].y=a[i].y; 195 ls(); 196 sortf(1,n); 197 solve(); 198 build(1,0,e[0]+1); 199 insert(1,0,0);insert(1,e[0]+1,e[0]+1); 200 for (int i=1;i<=n;i++) c[i].x=getnum(c[i].x),c[i].y=getnum(c[i].y); 201 for (int i=1;i<=n;i++) if (getl(1,c[i].x,c[i].y)==INF&&getr(1,c[i].x,c[i].y)==-INF){ 202 int ll=getr(1,0,c[i].x-1),rr=getl(1,c[i].y+1,e[0]+1); 203 if (query(ll+1,rr-1)==query(ll+1,c[i].x-1)+query(c[i].y+1,rr-1)+1) { 204 as[++ans]=i;insert(1,c[i].x,c[i].y); 205 } 206 } 207 208 printf("%d ",ans); 209 for (int i=1;i<=ans;i++) printf("%d ",as[i]); 210 return 0; 211 }
[BZOJ1179]Atm
Description

这大概是这套题目中最简单的一道了...
首先我们可以看出,题目中说的,可以经过一条边多次其实就是要处理环的情况
取款机里的钱都是非负整数,能拿的没有理由不要
因此如果进入了一个环,就可以把环中所有的钱都取光,然后从任意一个点出去
思路已经很明确了,tarjan缩点,同时累计每一个环的现金总数和是否存在一个酒吧
缩完点的图我们重新连上边(自环不连),就变成了一个有向无环图
我们可以用拓扑序DP来解决这个问题
对于给定的起点,这样类似的题目之前也做过
我的做法是先从起点开始dfs一次,重新统计入度
然后再进行DP,最后在那些有酒吧坐落的环或点答案中挑出一个最大的输出
1 /************************************************************** 2 Problem: 1179 3 User: mjy0724 4 Language: C++ 5 Result: Accepted 6 Time:6804 ms 7 Memory:52260 kb 8 ****************************************************************/ 9 10 #include<cstdio> 11 #include<cstdlib> 12 #include<cstring> 13 const int maxn = 500010; 14 int cnt,time,top,n,m,s,p,e,fa[maxn],next[maxn],link[maxn],x[maxn],y[maxn],b[maxn]; 15 int stack[maxn],low[maxn],dfn[maxn],pos[maxn],a[maxn],w[maxn],opt[maxn],f[maxn]; 16 bool vis[maxn],ins[maxn],isp[maxn],isbar[maxn]; 17 18 void add(int x,int y){ 19 fa[++e]=y;next[e]=link[x];link[x]=e; 20 } 21 22 int min(int a,int b){ 23 if (a<b) return a; 24 return b; 25 } 26 27 int max(int a,int b){ 28 if (a>b) return a; 29 return b; 30 } 31 void tarjan(int p){ 32 dfn[p]=low[p]=++time;stack[++top]=p; 33 vis[p]=false;ins[p]=true; 34 for (int i=link[p];i!=0;i=next[i]) 35 if (vis[fa[i]]){ 36 tarjan(fa[i]); 37 low[p]=min(low[p],low[fa[i]]); 38 }else if (ins[fa[i]]) low[p]=min(low[p],dfn[fa[i]]); 39 if (low[p]==dfn[p]){ 40 cnt++; 41 do{ 42 pos[stack[top]]=cnt; 43 a[cnt]+=w[stack[top]]; 44 isbar[cnt]=isbar[cnt] or isp[stack[top]]; 45 ins[stack[top--]]=false; 46 }while (stack[top+1]!=p); 47 } 48 } 49 50 void dfs(int p){ 51 vis[p]=false; 52 for (int i=link[p];i;i=next[i]){ 53 b[fa[i]]++; 54 if (vis[fa[i]]) dfs(fa[i]); 55 } 56 } 57 58 void solve(int s){ 59 int head=0,tail=1;opt[1]=s;f[s]=a[s]; 60 while (head!=tail){ 61 int x=f[opt[++head]]; 62 for (int i=link[opt[head]];i;i=next[i]){ 63 f[fa[i]]=max(f[fa[i]],x+a[fa[i]]); 64 b[fa[i]]--; 65 if (!b[fa[i]]) opt[++tail]=fa[i]; 66 } 67 } 68 int ans=0; 69 for (int i=1;i<=cnt;i++) if (isbar[i]) ans=max(ans,f[i]); 70 printf("%d ",ans); 71 } 72 int main(){ 73 scanf("%d%d",&n,&m); 74 e=0; 75 for (int i=1;i<=m;i++){ 76 scanf("%d%d",&x[i],&y[i]); 77 add(x[i],y[i]); 78 } 79 for (int i=1;i<=n;i++) scanf("%d",&w[i]); 80 scanf("%d%d",&s,&p); 81 memset(isp,false,sizeof(isp)); 82 for (int i=1;i<=p;i++){ 83 int tmp; 84 scanf("%d",&tmp); 85 isp[tmp]=true; 86 } 87 time=0;top=0; 88 memset(vis,true,sizeof(vis)); 89 memset(ins,false,sizeof(ins)); 90 memset(isbar,false,sizeof(isbar)); 91 for (int i=1;i<=n;i++) if (vis[i]) tarjan(i); 92 memset(link,0,sizeof(link)); 93 memset(next,0,sizeof(next)); 94 e=0; 95 for (int i=1;i<=m;i++) if (pos[x[i]]!=pos[y[i]]) add(pos[x[i]],pos[y[i]]); 96 memset(vis,true,sizeof(vis)); 97 dfs(pos[s]); 98 solve(pos[s]); 99 return 0; 100 }