线段树

众所周知，线段树这玩意又臭又长，但很容易理解。
线段树，有许多构造方法，我写的其实就是一棵完全二叉树，用堆式存储（也就是根节点的下标是1，每个下标(=k)父节点的左儿子就是(k * 2)，右儿子就是(k * 2 + 1)）。每个父节点的值就是她的两个子结点的值的和，叶子节点就是输入的序列，也就是我们写暴力用的那个序列。如下图：

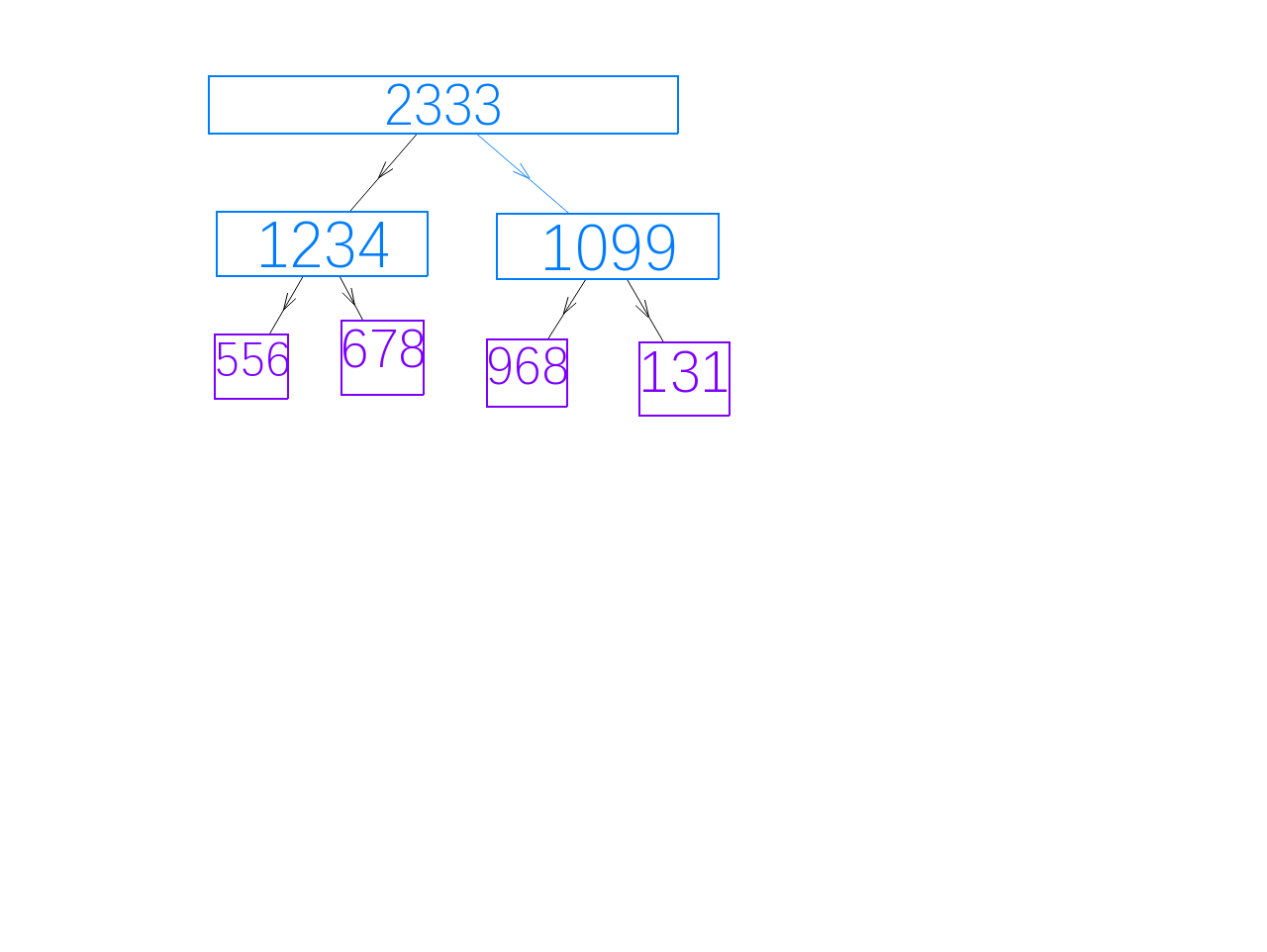
P.S.：紫色是叶子节点，也就是初始序列。
线段树一般有5个操作：建树、单点加、单点查询、区间加、区间查询（别问我区间乘怎么搞，我还在研究QwQ）。

建树：

我们要怎么把这个线段树建立起来呢？很简单，通过上面说的，只要从结点1开始递归，递归参数包括下标、控制的区间。其中控制的区间就是你这个点她所包括的范围。那么如果这个范围是1，就表示你已经到叶子结点了，就可以输入她的值了。而父节点则只要在递归完两个子树后将两个子节点的值相加即可。为了后面处理方便，我们定义数组(l[])、(r[])，表示结点k所控制的范围。具体实现如下：

inline void build(int ll,int rr,int k)//参数是：当前区间左边界、右边界，当前结点编号
{
	l[k]=ll,r[k]=rr;
	if(ll==rr)
	{
		scanf("%lld",&w[k]);
		return ;
	}
	int mid=(ll+rr)/2;
	build(ll,mid,k*2);
	build(mid+1,rr,k*2+1);
	w[k]=w[k*2]+w[k*2+1];
	return ;
}

单点加：

单点加也很简单，看懂了建树，就会发现单点加其实也差不多，就是从根节点开始，一直递归到相应的叶子结点，然后更改值，最后一路返回上来更改父节点的值。这个思路和二分查找十分向像。

inline void dadd(int k,int x,int y)//参数是：当前结点编号，要加的数的位置，要增加的值
{
	if(l[k]==r[k])
	{
		w[k]+=y;
		return ;
	}
    if(f[k]) down(k);
	int mid=(l[k]+r[k])/2;
	if(x<=mid) dadd(k*2,x,y);
	else dadd(k*2+1,x,y);
	w[k]=w[k*2]+w[k*2+1];
	return ;
}

单点查询：

在懂了单点加后，单点查询就更简单了，也是递归，也是二分的思路，而且还不用修改值。

inline int dsum(int k,int x)//参数是：当前结点编号，要查询的位置
{
	if(l[k]==r[k]) return w[k];
	if(f[k]) down(k);
	int mid=(l[k]+r[k])/2;
	if(x<=mid) return dsum(k*2,x);
	else return dsum(k*2+1,x);
}

区间查询：

诶，为什么不是区间加？因为区间加是重头戏，要放最后QwQ。区间查询和前面三个就大不相同了，但思路还是很好想的。想一下分块，处理一段区间，就是先把整的区间处理好，然后处理零碎的。线段树也一样，如果当前结点包含的范围都在查询区域内，那么就直接返回，否则，再考虑左右子节点，直到变成第一种情况。

inline int qsum(int ll,int rr,int k)//参数是：要查询的左边界、右边界，当前结点的编号
{
	if(l[k]>=ll&&r[k]<=rr) return w[k];
	if(f[k]) down(k);
	int mid=(l[k]+r[k])/2;
	int res=0;
	if(ll<=mid) res+=qsum(ll,rr,k*2);
	if(rr>mid) res+=qsum(ll,rr,k*2+1);
	return res;
}

区间加：

相信认证观察的同学已经发现了，前面除了建树，每个函数中都会出现if(f[k]) down(k);。而这个玩意的用处，就要在区间加中体现出来。区间加，思路和区间查询还是差不多的，不过这里我们要引入一个重点：懒惰标记。懒惰标记，顾名思义，要用的时候才动她，非常懒惰。懒惰标记分两种：下传型标记和永久性标记。这里只讲下传型标记（因为永久性我不会）。当你区间加递归到一个结点k，满足k所包含的范围都在区间加的范围内，那么我们就不用再递归下去了。为什么？观察上面的代码，发现每次要访问下面的结点都要先经过上面的，那么我们在走到上面的结点时再把这些数传到下面即可，非常方便。于是，我们又要开一个数组(f[])，存储懒惰标记。而下传操作的具体实现如下，具体看注释：

inline void down(int k)
{
	f[k*2]+=f[k];//把懒惰标记传下去，留给子子孙孙（划掉）下面的结点。
	f[k*2+1]+=f[k];//同上
	w[k*2]+=f[k]*(r[k*2]-l[k*2]+1);//根据结合律，就是这个玩意把数加上了QwQ。至于为什么要*f[k]……因为子节点本身也有可能之前就有懒标记啊。
	w[k*2+1]+=f[k]*(r[k*2+1]-l[k*2+1]+1);//同上
	f[k]=0;//清楚懒标记。
	return ;
}

那么，搞定了这个，区间加也不是什么难事了。

inline void qadd(int ll,int rr,int k,int x)//参数是：要加的区间的左边界、右边界，当前结点编号，要加的数。
{
	if(l[k]>=ll&&r[k]<=rr)
	{
		w[k]+=(r[k]-l[k]+1)*x;
		f[k]+=x;
		return ;
	}
	if(f[k]) down(k);
	int mid=(l[k]+r[k])/2;
	if(ll<=mid) qadd(ll,rr,k*2,x);
	if(rr>mid) qadd(ll,rr,k*2+1,x);
	w[k]=w[k*2]+w[k*2+1];//别忘了更新当前结点哦！
	return ;
}

总结：

如果有什么不懂的，可以尝试自己画个图模拟一下，很有用的。还有，数组要开四倍空间，至于为什么……自己画一个就知道了。
下面是总的连起来的代码。

struct tree
{
	int l[400005],r[400005];
	int w[400005],f[400005];
	inline void build(int ll,int rr,int k)
	{
		l[k]=ll,r[k]=rr;
		if(ll==rr)
		{
			scanf("%lld",&w[k]);
			return ;
		}
		int mid=(ll+rr)/2;
		build(ll,mid,k*2);
		build(mid+1,rr,k*2+1);
		w[k]=w[k*2]+w[k*2+1];
		return ;
	}
	inline void down(int k)
	{
		f[k*2]+=f[k];
		f[k*2+1]+=f[k];
		w[k*2]+=f[k]*(r[k*2]-l[k*2]+1);
		w[k*2+1]+=f[k]*(r[k*2+1]-l[k*2+1]+1);
		f[k]=0;
		return ;
	}
	inline void dadd(int k,int x,int y)
	{
		if(l[k]==r[k])
		{
			w[k]+=y;
			return ;
		}
		if(f[k]) down(k);
		int mid=(l[k]+r[k])/2;
		if(x<=mid) dadd(k*2,x,y);
		else dadd(k*2+1,x,y);
		w[k]=w[k*2]+w[k*2+1];
		return ;
	}
	inline void qadd(int ll,int rr,int k,int x)
	{
		if(l[k]>=ll&&r[k]<=rr)
		{
			w[k]+=(r[k]-l[k]+1)*x;
			f[k]+=x;
			return ;
		}
		if(f[k]) down(k);
		int mid=(l[k]+r[k])/2;
		if(ll<=mid) qadd(ll,rr,k*2,x);
		if(rr>mid) qadd(ll,rr,k*2+1,x);
		w[k]=w[k*2]+w[k*2+1];
		return ;
	}
	inline int dsum(int k,int x)
	{
		if(l[k]==r[k]) return w[k];
		if(f[k]) down(k);
		int mid=(l[k]+r[k])/2;
		if(x<=mid) return dsum(k*2,x);
		else return dsum(k*2+1,x);
	}
	inline int qsum(int ll,int rr,int k)
	{
		if(l[k]>=ll&&r[k]<=rr) return w[k];
		if(f[k]) down(k);
		int mid=(l[k]+r[k])/2;
		int res=0;
		if(ll<=mid) res+=qsum(ll,rr,k*2);
		if(rr>mid) res+=qsum(ll,rr,k*2+1);
		return res;
	}
}tr;

对了，代码里我基本没有写注释，是因为我懒如果没有注释你也看得懂的话就说明你已经学会97%了，再自己手打一遍，就可以100%理解并学会了！