完全背包的话 就是说每一个背包都有n个可以放进
for(i=1;i<=row;i++) { for(j=1;j<=col;j++) { int temp = j/w[i]; for(int k = 1; k <= w[i]; ++k) //最多能装下多少个i物品 依次判断 { dp[i][j] = max(dp[i][j],dp[i-1][j-w[i]*k] + k*w[i]); } } }
这个复杂度比较高
我们进行了优化
递归方程可以写成 dp[i][j] = max(dp[i][j],dp[i][j-w[i]] + v[i]);
优化的方法:
1、dp[i][j] = max(dp[i-1][j],dp[i-1][j-w[i]] + v[i],dp[i-1][j-2*w[i]]+2*v[i],...........)
2、dp[i][j-w[i]] = max(dp[i-1][j-w[i], dp[ i-1 ][ j-w[i]-w[i] ] + v[i])
3、dp[i][j] = max(dp[i-1][j],dp[i][j-w[i]],........) //2式替换1式中的前两项
同理后面接着写
其实还是画图好理解:
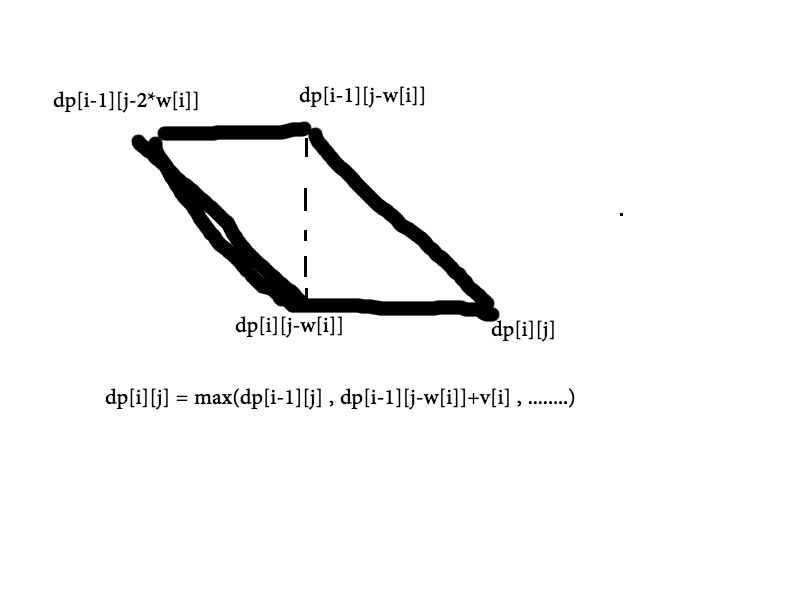
复杂度O(vn)
这个图好像也能解答下面的东西。
初始化的细节问题:
有的问题中有要求“恰好装满背包”,有的则没有要求,这就在初始化DP数组时有所不同。
恰好装满背包:则初始化时,DP[0]=0, 其他的DP[1…..V]均设为负的无穷大。
无须恰好装满背包:则初始化时,DP[1…..V]全部设为0;