1.题目:

设计思想:首先字符串的输入运用nextInt转换就可以,进行输入即可。这道题目主要是判断是否为回文字符串的那部分,可以将方法定义在主函数中,也可以定义在主函数外进行调用。判断部分:.length()判断长度,.charAt()接收字符,关键是控制进程的算法,因为是回文字符串,所以判断的是对应位置,找到准确的对应位置是关键,
a=str.length()-n; b=str.length()-(a+1); 两者一个从头开始,一个从尾部开始,开始相向而行,两者控制对应位置,下面运用递归算法 一遍又一遍判断对应位置的值是否一样,当两者一样,进行一次确定,只有一个字符就是回文数的判断等。
流程图:
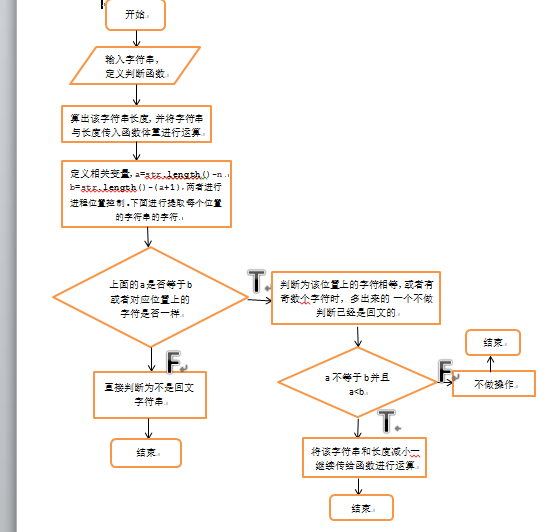
程序代码:
//使用递归方式判断某个字串是否是回文
import java.util.*;
public class Huiwenzifuchuan
{
public static void main(String[] args)
{
System.out.println("请输入字符串:");
Scanner reader=new Scanner(System.in);
String str=reader.next();
int n=str.length();//测定字符串的长度,区分数组判断长度的,测定数组的没有括号
int m=huiwen(str,n);
if(m==1)
System.out.println("这个字符串是回文字符串!");
else
System.out.println("这个字符串不是回文字符串!");
}
public static int huiwen(String str,int n)
{
int a,b,j=0;
char c1,c2;
a=str.length()-n;//控制进程 从第一个开始正向移动
b=str.length()-(a+1);//从最后一个开始倒着移动
c1=str.charAt(a);//取字符的函数
c2=str.charAt(b);
if(c1==c2||a==b) j=1;//判断 如果相应的字符一样 J=1,//奇数个字符时 多出来的一个 不用递归判断 直接是回文字符串
if(a!=b&&a<b&&j==1)
huiwen(str,n-1);//递归 判断下一对字符 并且a和b正向判断一次后就不必让a和b走到尽头继续判断 两者达到终点即可
//if(a==b) j=1;//奇数个字符时 多出来的一个 不用递归判断 直接是回文字符串)
return j;
}
}
程序运行截图:
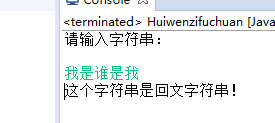
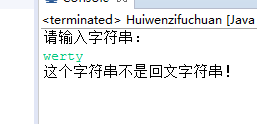
2.题目:
![]()
(1)第一种:.使用组合数公式利用n!来计算:
设计思路:因为可能是大数据的阶乘,所以直接用大数据类来计算阶乘,只要阶乘计算出来了,总的结果乘除就出来了。在计算阶乘时,使用用递归的方法即可,设置出递归函数结束时的条件,下面直接计算递归即可。最后将结果直接运用于计算组合数的函数中,因为是大数据,所以加减乘除要用大数据的计算方法,计算方法如下:

程序流程图:
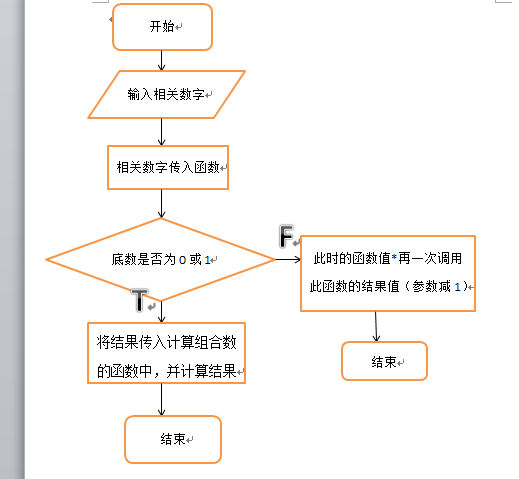
源程序代码:
//第一小题:使用计算机计算组合数:使用组合数公式利用n!来计算
import java.math.BigInteger;
import java.util.*;
public class Elementary
{
public static void main(String[] args)
{
Scanner reader=new Scanner(System.in);
System.out.println("输入n和k: ");
int n=reader.nextInt();
int k=reader.nextInt();
System.out.println(combination(n,k));
}
public static BigInteger jiecheng(int num)
{
if(num==1||num==0)
{
return BigInteger.valueOf(1);
}
return BigInteger.valueOf(num).multiply(jiecheng((num-1))); //大数据计算组合数的方法
}
public static BigInteger combination(int n,int k)
{
BigInteger i;
BigInteger j;
BigInteger m;
i=jiecheng(n);
j=jiecheng(k);
m=jiecheng(n-k);
return i.divide(j.multiply(m));//大数据之间的加减乘除计算方法
}
}
程序运行结果截图:

(2)第二种方法:使用递推的方法用杨辉三角计算
设计思路:输入该输入的数值,传入函数中计算。首先第一个函数,我写的是一个计算杨辉三角的函数,杨辉三角哦用的是二维数组来算,注意每一行和最后一行的数字都是1,要进行设置,之后运用for循环的嵌套计算出杨辉三角,然后根据递推公式,找出相应位置上的数字进行相加推算出总结果即可。
程序流程图:
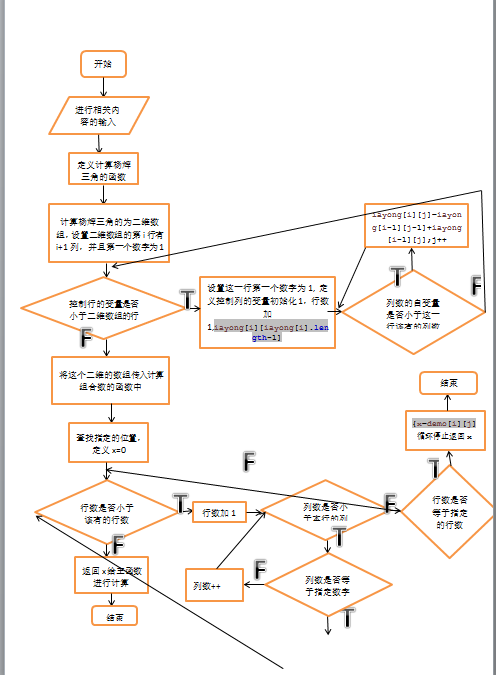
源程序代码:
//第二小题:使用递推的方法用杨辉三角验证了这个式子 也得到了正确的答案 这个程序也进行了验证
import java.math.BigInteger;
import java.util.*;
public class Yanghui
{
public static void main(String[] args)
{
System.out.println("输入行数n和第几个数k(这也是用来计算组合数的): ");
Scanner reader=new Scanner(System.in);
int n=reader.nextInt();
int k=reader.nextInt();
int i=shuchu(n-1,k-1);//计算组合式的后两项的前一项的值
int m=shuchu(n-1,k);//计算组合式的后两项的后一项的值
BigInteger j = combination(n,k);//已经计算好的组合数
System.out.println("使用杨辉三角计算的组合式的后两项的值和两值的总和分别是是:"+i+" "+m+" "+(i+m));
System.out.println("使用组合数公式计算的值是:"+j);
System.out.println("上式得证!");
}
public static int[][] yanghuisanjiao()//计算杨辉三角
{
int i,j;
int[][]iayong=new int[1000][];
for( i=0;i<iayong.length;i++)
{
iayong[i]=new int[i+1];//定义二维数组的第i行有i+1列
}
iayong[0][0]=1;
for(i=1;i<iayong.length;i++)//计算杨辉三角形
{
iayong[i][0]=1;
for(j=1;j<iayong[i].length-1;j++)
iayong[i][j]=iayong[i-1][j-1]+iayong[i-1][j];//杨辉三角形规律
iayong[i][iayong[i].length-1]=1;
}
return iayong;
}
public static int shuchu(int n,int k)//利用杨辉三角计算某个位置上的数字
{
int[][]demo=new int[1000][];
int x = 0,j;
demo=yanghuisanjiao();
for(int i=0;i<demo.length;i++)
{//for循环用来寻找指定位置
for(j=0;j<demo[i].length;j++)
{
if(j==k) break;
}
if(i==n) {x=demo[i][j];break;}//查找指定位置上的数字
}
return x;
}
//下面两个函数用来计算组合数 大数据的计算方式
public static BigInteger jiecheng(int num)
{
if(num==1||num==0)
{
return BigInteger.valueOf(1);
}
return BigInteger.valueOf(num).multiply(jiecheng((num-1)));
}//计算阶乘
public static BigInteger combination(int n,int k)
{
BigInteger i;
BigInteger j;
BigInteger m;
i=jiecheng(n);
j=jiecheng(k);
m=jiecheng(n-k);
return i.divide(j.multiply(m));
}//计算组合数
}
运行结果截图:

(3)第三种:是用递归的方法用组合数递推公式计算:
设计思路:输入相应的数值,传入方法中进行计算,方法为是用递归的方法,当就算的数值即输入的数值不等时,继续调用方法进行计算,只不过相应的数字减1,直到找到可以停止的位置,停止的条件是组合数的取得计算数值等于1时返回总数值,或者总数值等于计算数值。
程序流程图:
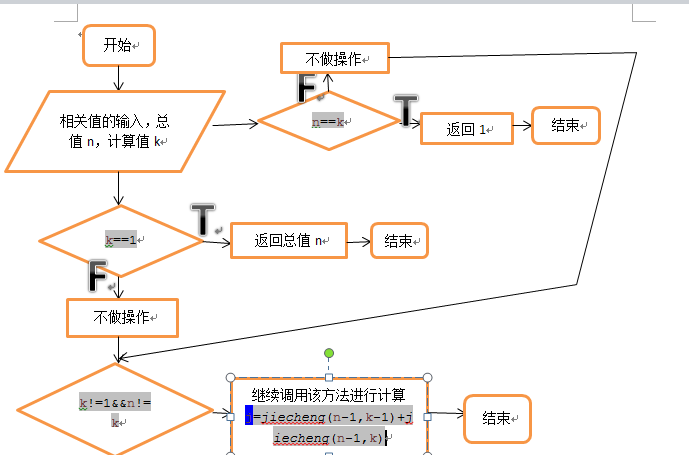
源程序代码:
//第三小题:使用递归方法用组合数递推公式计算得到
import java.util.*;
public class Diguizuhe {
public static void main(String[] args)
{
Scanner reader=new Scanner(System.in);
System.out.println("输入n和k: ");
int n=reader.nextInt();
int k=reader.nextInt();
System.out.println("使用递归方法用组合数递推公式计算得到: "+jiecheng(n,k));
}
public static long jiecheng(int n,int k)
{
long j=0;
if(k==1) return n;
if(n==k) return 1;
if(k!=1&&n!=k)
j=jiecheng(n-1,k-1)+jiecheng(n-1,k);
return j;
}
}
程序运行结果截图:

3.汉诺塔问题:
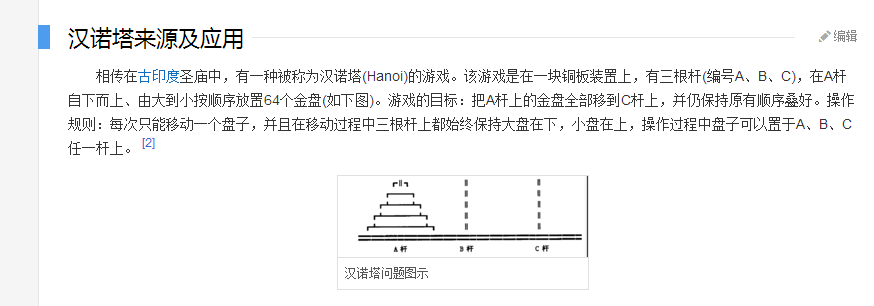
设计思路:
要将最大的盘子移至C柱,那么必然要先搬掉A柱上面的n-1个盘子,而C柱一开始的时候是作为目标柱的,所以我们可以用B柱作为"暂存"这n-1个盘子的过渡柱,当把这n-1的盘子移至B柱后,我们就可以把A柱最底下的盘子移至C柱了。现在将移动这n-1个盘子到目标柱子,此时A柱上无盘子,而B柱从上到下依次摆放着从小到大的n-1个盘子,C柱上摆放着最大的那个盘子。所以那就是要把B柱这剩下的n-1个盘子移至C柱,而B柱作为过渡柱,那么我们需要借助A柱,将A柱作为新的"过渡"柱,将这n-1个盘子移至C柱。
程序流程图:
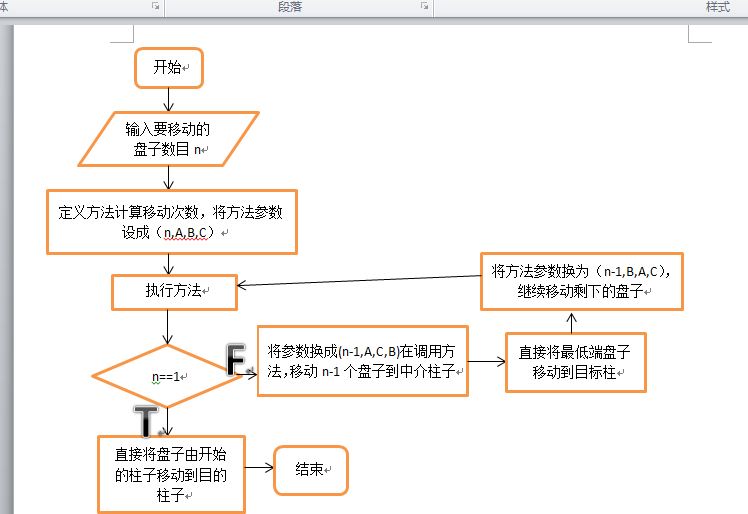
程序源代码:
/*第二题:汉诺塔问题 首先A作为起始柱,现将第n个移至C,这时B作为过度柱,成功后,B柱从上到下依次摆放着从小到大的n-1个盘子,C柱上摆放着最大的那个盘子。
所以接下来的问题就显而易见了,那就是要把B柱这剩下的n-1个盘子移至C柱,而B柱作为过渡柱,那么我们需要借助A柱,将A柱作为新的"过渡"柱,将这n-1个盘子移至C柱。*/
import java.util.*;
public class Hannuota
{
static int i=0;
public static void main(String[] args)
{
System.out.println("请输入你要移动多少个盘子: ");
Scanner reader=new Scanner(System.in);
int n=reader.nextInt();
jisuan(n,'1','2','3');
reader.close();
}
public static void jisuan(int n,char A,char B,char C)
{
if(n==1) move(n,A,C);//只有一个直接由开始的柱子移动到目标柱子
else
{
jisuan(n-1,A,C,B);//一开始都在A注,A作为开始柱,先将n-1个移动到B 这时B作为目标柱 再将最下面的移动到目标柱子C
move(n,A,C);//将第N个移动到C 目标柱子,完成一次
jisuan(n-1,B,A,C);//这时进行下一次为n-1个盘子的移动,这时盘子都在B柱子,所以这时B作为起始柱 A作为中间的柱子 ,C柱子还是最终目标柱子
}
}
public static void move(int n,char from,char to)
{
System.out.println("第"+(++i)+"步,将"+n+"号盘子从"+from+"移动到"+to);
}
}
程序运行结果截图:
