到目前为止,我们所提过的所有数据结构,不是线性表,就是树。即使是散列表、优先队列、AVL树这样看似特殊的数据结构,其实也没逃出线性表与树的范畴,那么,在数据结构方面(如果是说算法方面,那么与线性表、树相关的算法可讲不完),还有什么我们尚未探讨的情况吗?
答案是肯定的,那就是:图。不过在进一步介绍图之前,我想先回顾一下树与线性表的关系。不难发现,其实线性表就是一棵特殊的树:“无叉树”。而树也可以看作是将线性表要求放宽后得出的数据结构:元素的后继个数不再有限制。那么,将“放宽要求”的思想再次应用于树之上,我们可以得出什么样的数据结构呢?那就是图:
1.元素的前驱,即父亲的个数不限(树中有限制)
2.元素的后继,即孩子的个数不限
3.元素X可以既是Y的前驱,又是Y的后继。(树中有限制)
不过需要注意的是,如果一个元素既没有前驱也没有后继,那它是一个“独立”的“集合”,换句话说就是一个无前驱也无后继的元素不属于某个已存在的图。这一点在树、线性表中也是一样的。
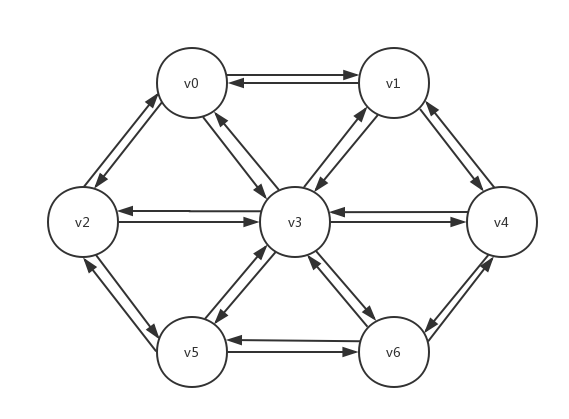
下面是一个图的例子:

上例中的图,既有无前驱的元素:v0,也有无后继的元素:v5,而v3则显然是一个有多前驱、多后继的元素。
上例中的图体现出了图的第1、2条特点,而下面的图则体现出了图的第3个特点:
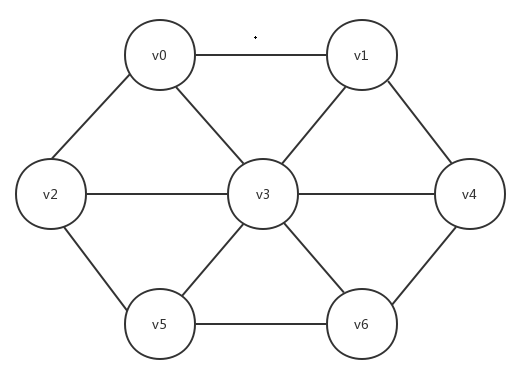
在第一个例子的基础上,我们令每个元素都成为自己前驱的前驱,从而有了第二个例子。
图的直观概念有了之后,我们接下来要谈一下和图相关的一些术语。首先,在图中,我们将元素称作“顶点”(vertex,例子中的v即其简写),而顶点间的“有箭头的线段”我们称之为“有向边”,有向边由两个顶点确定并表示:(vx,vy),其中vx表示有向边的起点,vy表示有向边的终点。
有向边(vx,vy)和其反向边(vy,vx)可以结合起来作为一条“无向边”,或者叫“双向边”,如果图中任意一条边都有反向边,或者说所有边都是无向边,那么我们称这个图是“无向图”,否则是“有向图”,显然第二个例子是一个无向图,第一个例子不是。而对于无向图,我们可以以更简单的形式将其画出,即将所有有向边与其反向边结合为一条边,并去掉箭头,比如第二个例子可以画作这样:
图的可能用处是显而易见的,城市间公路地图就可以用无向图来模拟,用顶点代表城市,无向边表示两个城市间的公路。而一项工程的流程则可以用有向图来模拟:可能某步骤需要先完成其他几个步骤才能做,比如组装发动机得在制造好活塞、缸体等组件后才能进行,这就是“多前驱”的情况,也可能好多个步骤都需要等某个步骤做完后才能继续,比如安装轮胎、安装座椅等工作都得在车架制造好之后才能进行,这就是“多后继”的情况。
知道了图的概念和可能用处之后,下一个问题是:如何存储一个图?首先需要明确的是,无向图总是可以用有向图来表示,只要将一条无向边拆成两条方向相反的有向边即可。所以我们只要关注如何存储有向图,就可以顺带解决无向图的存储问题。
一个简单的想法是假设所有顶点用自然数从0开始逐一编号,然后构造一个二维数组:
bool graph[numVertex][numVertex];
其中graph[x][y]若为true,则表示存在有向边(x,y),否则表示不存在有向边(x,y)。而无向边[a,b]则可以拆成有向边(a,b)和(b,a),从而实现存储。
如果采用这样的方式存储图,那么我们第一个例子中的有向图将会这样存储(v0-v6对应下标0-6,纵向为数组一维下标,横向为二维下标):

而第二个例子中的有向图则可以这样存储:

这样的存储方式我们称之为邻接矩阵(两个顶点之间存在边即这两个顶点邻接)。邻接矩阵简单、快捷,但是存在很大的浪费,对于第一个例子,可以说我们用了49个变量,却只有12个(约24.5%)真正起了作用,剩下37个(约75.5%)都是“用了真实的内存来表示不存在的东西”,即便是对于第二个例子,我们也浪费了一半的空间。所以,如果图不够“稠密”(即边的数量接近顶点数量的平方),我们一般不采用邻接矩阵来存储图,而是用邻接表来存储图。文字表达邻接表是什么非常麻烦,也不容易懂,所以我们先直接给出第一个例子用邻接表存储的抽象表示,再来解释邻接表的实现方法:
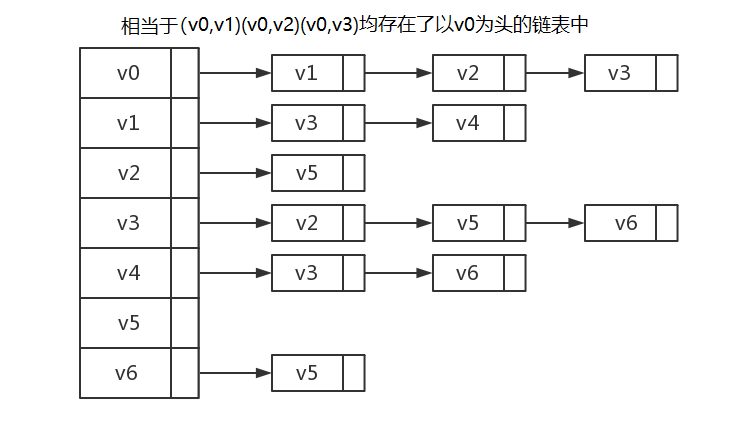
从上图可以看出,邻接表长得非常像分离链接式的散列表,首先我们依然假设顶点用数字表示,然后我们用一个数组graph来存储所有顶点(图中左侧),接着对于每一条有向边(x,y),我们创建一个“代表y的结点”,然后将该结点插入到以graph[x]为头的链表中去,抽象理解即将边(x,y)插入了进去:
//"结点"的定义 typedef struct node{ size_t vertex; struct node *next; }Node; //存储所有顶点的数组(即图) //所有以顶点x作为起点的有向边的终点,均存储在以graph[x]为头的链表中 Node *graph[numVertex]; //边的定义 typedef struct edge{ size_t start; size_t end; }Edge; /*构造图的函数,假设所有边已放入数组allEdges,graph数组的大小是正确的,且graph数组每个元素都已初始化为NULL,numEdge为边的个数*/ void buildGraph(Node **graph,Edge *allEdges,size_t numEdge) { size_t start; Node *newNode; for(int i=0;i<numEdge;++i) { start=allEdges[i].start; newNode=(Node *)malloc(sizeof(Node)); newNode->vertex=allEdges[i].end; newNode->next=graph[start]; graph[start]=newNode; } }
这样一来,所有以x为起点的边(x,y)都可以通过遍历以graph[x]为头的链表来找到,不过在该链表中我们只存储了边的终点y,因为起点就是链表头的下标。
如果需要令图支持动态变化,那么将graph数组转换成一个链表即可,方便起见,我们暂且用数组来存储顶点。
接下来我们要讨论的东西是拓扑排序。但是在讨论拓扑排序前,有两个概念需要理解:路径、圈。所谓路径,就是从图中某个顶点出发,沿着边,到达另一个顶点后,经过的边的集合。举例来说,看下图

这个图中,从v0到v6的路径可以是:
(v0,v3)-(v3,v6)
简写成这样也行,只要能表达出意思即可:
v0-v3-v6
显然,从一个顶点到另一个顶点的路径可能不止一条,比如上图中v0到v6还可以这样走:v0-v1-v4-v6
路径的长度一般用路径中边的条数表示,比如路径v0-v3-v6长度不是3,而是2。此外,v0-v0我们也认为是一条路径,其长度为0。
那么什么是圈呢?圈就是一种特殊的路径,该路径的起点和终点是同一个顶点,而且路径长度大于0(也就是说路径vx-vx不算圈,我们称之为“环”)。比如下图
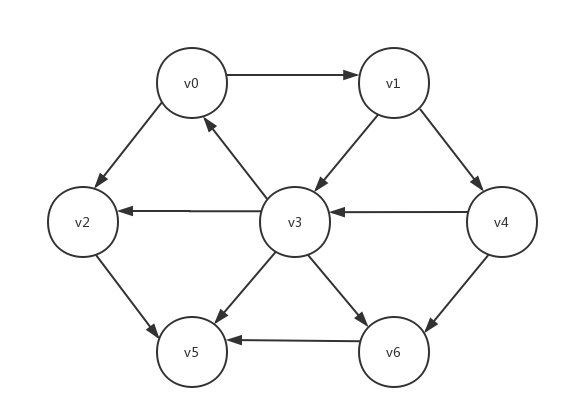
其中路径v0-v1-v4-v3-v0就是一个圈。
知道了什么是圈后,我们就可以开始讨论拓扑排序了。拓扑排序就是对图中顶点进行的排序,其要求是:若存在从vx到vy的路径,那么排序结果中vx必须在vy之前。这个要求其实就暗含着另一个要求,那就是:进行拓扑排序的图必须是有向无圈图。在无向图中,若存在边(vx,vy)则必存在边(vy,vx),那么依拓扑排序的要求,vx就必须在vy的前面,同时vy又必须在vx前面,这显然是矛盾的,所以拓扑排序只能用于有向图。而在有向有圈图中,比如上图,其中的圈v0-v1-v4-v3-v0就暗含着两条子路径:v0-v1-v4和v4-v3-v0,依前一条路径而言,排序结果中v0必须在v4前面,而依后一条路径而言,v4又必须在v0前面,这显然也是矛盾的,所以拓扑排序只能用于有向无圈图。
接下来对拓扑排序的讨论依照下图进行

显然上图是一个有向无圈图,那么其拓扑排序之一是这样的:
v0,v1,v4,v3,v2,v6,v5
注意,一个图的拓扑排序结果可能不是唯一的,比如上图的另一个拓扑排序结果是:
v0,v1,v4,v3,v6,v2,v5
有了拓扑排序结果后,我们可以试着换一个角度来理解拓扑排序:对于排序结果中的任意两个顶点vx和vy,若vy在vx之后,则图中必然没有从vy到vx的路径。
可是,洋洋洒洒说了那么多,拓扑排序有什么用呢?前面我们说过,工艺流程可以用有向图来模拟,那么如果我们对一个工艺流程图进行拓扑排序,我们就能确定各个步骤按照怎样的顺序去做就绝对不会出现做完了一个步骤,却因为还有某个步骤没完成,从而不能做下一个步骤的情况。类似的,游戏中的任务系统也可以用图模拟,比如一些游戏中存在隐藏任务,可能一个隐藏任务需要完成多个普通任务才会触发,而只有完成了这个隐藏任务,你才可以去接收更多的隐藏任务,此时也可能运用到拓扑排序。
总而言之,如果我们有步骤A和B,且A需要在B之前完成,那么我们就可以将A、B视为顶点,B对A的“依赖关系”视为边(A,B),当我们知道大量的步骤和局部的依赖关系时,我们就可以将其构建成一个完整的图,然后通过拓扑排序确定整体的依赖关系。当然,拓扑排序也可以用于判断一个图有没有圈,并且后面对图的进一步讨论时我们也将利用拓扑排序实现一些改进。
接下来的问题显然就是如何实现拓扑排序,在说明如何进行拓扑排序之前,我们先了解一下有向无圈图的两个特点:
1.若图有向无圈,则必然存在一个入度为0的顶点。
2.若图有向无圈,则去掉其入度为0的顶点及相连边(必为以该顶点为起点的有向边)后,图依然是有向无圈图。
所谓顶点的入度,即以该顶点为终点的有向边个数,比如顶点vy的入度即边(vx,vy)的个数(其中x!=y)。
知道了有向无圈图的特点后,一种简单的拓扑排序思路就出来了:在用有向边表示依赖关系的图中,若一个顶点的入度为0,就说明该顶点不依赖其他顶点,所以这个顶点可以直接输出到排序结果中,而这个顶点输出了,就意味着其所代表的步骤“做完了”,所以依赖于其的顶点不再依赖于其,可将其相连边均去除,然后再找图中的下一个入度为0的顶点。
用代码来表示就是这样(蓝色字体为伪代码):
void topSort(graph* g,size_t numVertex,size_t topResult) { //两个表示顶点的变量,后面用 size_t tempV,adjV; //存储各顶点入度的数组,顶点x的入度为indegree[x] size_t indegree[numVertex]; 伪:根据图g初始化indegree数组 for(int i=0;i<numVertex;++i) { 伪:从indegree中找到一个入度为0的顶点,存入tempV if(伪:没找到入度为0的顶点) 伪:报错、返回 topResult[i]=tempV; 伪:通过g[tempV]遍历tempV为起点的边的终点,存入adjV indegree[adjV]--; } }
显然,上述拓扑排序算法还有一定的改进空间,我们在寻找入度为0的顶点时每次都要遍历整个indegree数组,这使得整个算法的时间复杂度达到了O(n2)(n为顶点个数)。然而实际上我们可以先遍历一次indegree数组,然后将找到的所有入度为0的顶点存入一个队列中,然后通过队列出队来获取入度为0的顶点,而当我们减少某个顶点的入度时(indegree[adjV]--时)则判断一下它是否已达到入度为0,若是则将其入队。
void topSort(graph* g,size_t numVertex,size_t topResult) { //两个表示顶点的变量,后面用 size_t tempV,adjV; //存储各顶点入度的数组,顶点x的入度为indegree[x] size_t indegree[numVertex]; 伪:根据图g初始化indegree数组 伪:根据indegree数组,创建一个zeroIndegree队列,队列中的顶点入度为0 size_t i=0; while(伪:zeroIndegree不为空) { tempV=Dequeue(zeroIndegree); topResult[i]=tempV; 伪:通过g[tempV]遍历以tempV为起点的边的终点,存入adjV { indegree[adjV]--; if(indegree[adjV]==0) Inqueue(zeroIndegree,adjV); } }
if(i!=numVertex-1)
伪:报错
}
这样一来,拓扑排序的时间复杂度就降到了O(nv+ne)(nv为顶点个数,ne为边条数)。
作为本文的结尾,我们最后来说一说一个不容忽视的问题:如果图的元素的关键字不是自然数怎么办?很直白的想法是,如果元素的关键字不是自然数(比如字符串),我们就将其转换为自然数。实现这一点的方法就是通过散列表得出元素关键字的散列值,而后用该散列值(即顶点)代表该元素。不过这样做又会带来另一个问题:如何根据顶点(即散列值),找回对应元素的关键字?这个问题的粗暴解法就是,在将元素插入到散列表中时,将元素在散列表中的内存地址存下来,比如存入一个名为inverseHash的链表中,而后在需要时通过inverseHash来找到一个顶点(散列值)所对应元素的位置。此外,因为元素的散列值可能并非按自然数顺序生成的,所以存储顶点时也不该再使用graph数组,而应该将其改为其他数据结构(链表甚至树)。当然,还有其他的存储思路,但根本思想都是基于邻接表:先存储所有顶点,再将以某顶点为起点的边存储到以该顶点为头的数据结构中。
在介绍图的可能用处时,我们不仅提到了图可以表示工艺流程,还提到了图可以表示“本来就是图”的地图,而对于表示地图的图,一个很明显的问题就是:如何找到两个顶点间的最短路径?这个问题我们在下一篇博客介绍解决方法。