树的遍历——c#实现

　　树作为一种重要的非线性数据结构，以分支关系定义其层次结构，在客观世界中应用广泛。通过对树遍历，将树进行线性化处理，即遍历的结果是将非线性结构的树种节点排列成一个线性序列。其中，最常见的遍历方式包括先序、中序、后序遍历3种。此外，还有一种按照“从上到下，从左到右”的层次遍历方式。

　　以下列二叉树为例，对其进行遍历及实现。

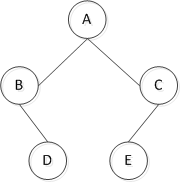
1 先序遍历

1.1 遍历操作　　

　　先序遍历二叉树的操作定义如下：

　　若二叉树为空，则操作空，否则

• 先访问树的根节点
• 再遍历左子树
• 遍历右子树

　　上例遍历结果为：ABDCE

1.2 遍历实现　　　　

　　前序遍历的递归实现如下：

//递归实现前序遍历
public static void preorder(Node root)
        {
           if (root == null)
            {
                return;
            }
           Console.Write("{0}  ", root.value);
           preorder(root.left);
           preorder(root.right);
        }

//非递归前序遍历 
public static void preOrder_Nonrec(Node root)
        {
            Console.Write("前序遍历为：");
            Stack<Node> st = new Stack<Node>();
            st.Push(root);
            while (st.Count != 0)
            {
                Node cur = st.Pop();
                Console.Write("{0}", cur.value);
                if (cur.right != null)
                {
                    st.Push(cur.right);
                }
                if (cur.left != null)
                {
                    st.Push(cur.left);
                }
            }
            Console.WriteLine();
        }

2 中序遍历

2.1 操作定义

　　中序遍历二叉树的操作定义如下：

　　若二叉树为空，则操作空，否则

• 先遍历树的左子树
• 访问根节点
• 遍历右子树

2.2 中序遍历实现　　

//递归实现二叉树中序遍历
 public static void midOrder(Node root){
           
            if (root == null)
            {
                return;
            }
            midOrder(root.left);
            Console.Write("{0}  ", root.value);
            midOrder(root.right);
        }

//非递归实现二叉树中序遍历

public static void inOrder_nonrec(Node root)
        {
            Console.Write("中序遍历为：");
           if(root!=null){
                Stack<Node> st = new Stack<Node>();
                while(st.Count!=0 || root!=null){
                    if(root!=null){
                        st.Push(root);
                        root=root.left;
                    }else{
                        root=st.Pop();
                        Console.Write("{0}",root.value);
                        root=root.right;
                    }
                }
            }

3 后序遍历

3.1 操作定义

　　后序遍历二叉树的操作定义如下：

　　若二叉树为空，则操作空，否则

• 遍历树的左子树
• 遍历右子树
• 访问根节点

3.2 后序遍历实现　

//递归实现后序遍历
public static void postOrder(Node root)
        {
           if(root ==null){
                return;
            }
            postOrder(root.left);
            postOrder(root.right);
            Console.Write("{0}  ", root.value);
        }

//非递归实现后序遍历
public static void post_nonrec(Node root)
        {
            Console.Write("后序遍历为：");
            if(root!=null){
                Stack<Node> s1 = new Stack<Node>();
                Stack<Node> s2 = new Stack<Node>();
                s1.Push(root);
                while(s1.Count!=0){
                    root = s1.Pop();
                    s2.Push(root);
                    if(root.left!=null){
                       s1.Push(root.left);
                    }
                    if (root.right != null)
                    {
                        s1.Push(root.right);
                    }
                }
                while(s2.Count!=0){
                    Console.Write("{0}",s2.Pop().value);
                }
            }
        }

整体代码

namespace treeTrace
{
    class Program
    {
        static void Main(string[] args)
        {
            Node nodeA = new Node(1);
            Node nodeB = new Node(2);
            Node nodeC= new Node(3);
            Node nodeD = new Node(4);
            Node nodeE= new Node(5);
            Node.buileTree(ref nodeE,nodeC,null,null);
            Node.buileTree(ref nodeD,nodeB,null,null);
            Node.buileTree(ref nodeC,nodeA,nodeE,null);
            Node.buileTree(ref nodeB,nodeA,null,nodeD);
            Node.buileTree(ref nodeA,null,nodeB,nodeC);
            //递归实现
            Console.Write("前序遍历为：");
            Node.preorder(nodeA);
            //Console.Write("中序遍历为：");
            //Node.midOrder(nodeA);
            //Console.Write("后序遍历为：");
            //Node.postOrder(nodeA);
            //非递归实现
           // Node.preOrder_Nonrec(nodeA);
            //Node.inOrder_nonrec(nodeA);
           // Node.post_nonrec(nodeA);
            Console.Read();
        }
    }
    public class Node
    {
        public int value;
        public Node _root;
        private Node _left;
        public Node _right;
        public Node root
        {
            get { return _root; }
            set { _root = value; }
        }
        public Node left
        {
            get { return _left; }
            set { _left = value; }
        }
        public Node right
        {
            get { return _right; }
            set { _right = value; }
        }

        public Node(int data)
        {
            this.value = data;
        }
        //创建二叉树
        public static void buileTree(ref Node node,Node root,Node left,Node right)
        {
            node.left=left;
            node.right=right;
            node.root = root;
        }
        //public static void build(Node root)
        //{
        //    if (root == null)
        //        return;
        //    build(root.left);
        //    build(root.right);
        //}

        #region 递归实现前序、中序、后序遍历
        public static void preorder(Node root)
        {
           if (root == null)
            {
                return;
            }
           Console.Write("{0}  ", root.value);
           preorder(root.left);
           preorder(root.right);
        }
        public static void midOrder(Node root){
           
            if (root == null)
            {
                return;
            }
            midOrder(root.left);
            Console.Write("{0}  ", root.value);
            midOrder(root.right);
        }
        public static void postOrder(Node root)
        {
           if(root ==null){
                return;
            }
            postOrder(root.left);
            postOrder(root.right);
            Console.Write("{0}  ", root.value);
        }
        #endregion

        #region 非递归实现树的前序、中序、后序遍历

        public static void preOrder_Nonrec(Node root)
        {
            Console.Write("前序遍历为：");
            Stack<Node> st = new Stack<Node>();
            st.Push(root);
            while (st.Count != 0)
            {
                Node cur = st.Pop();
                Console.Write("{0}", cur.value);
                if (cur.right != null)
                {
                    st.Push(cur.right);
                }
                if (cur.left != null)
                {
                    st.Push(cur.left);
                }
            }
            Console.WriteLine();
        }
        public static void inOrder_nonrec(Node root)
        {
            Console.Write("中序遍历为：");
           if(root!=null){
                Stack<Node> st = new Stack<Node>();
                while(st.Count!=0 || root!=null){
                    if(root!=null){
                        st.Push(root);
                        root=root.left;
                    }else{
                        root=st.Pop();
                        Console.Write("{0}",root.value);
                        root=root.right;
                    }
                }
            }
            Console.WriteLine();
         }
        public static void post_nonrec(Node root)
        {
            Console.Write("后序遍历为：");
            if(root!=null){
                Stack<Node> s1 = new Stack<Node>();
                Stack<Node> s2 = new Stack<Node>();
                s1.Push(root);
                while(s1.Count!=0){
                    root = s1.Pop();
                    s2.Push(root);
                    if(root.left!=null){
                       s1.Push(root.left);
                    }
                    if (root.right != null)
                    {
                        s1.Push(root.right);
                    }
                }
                while(s2.Count!=0){
                    Console.Write("{0}",s2.Pop().value);
                }
            }
        }
        #endregion

       
    }
}