高等数理统计（四）

引言

　　【比较官方的简介】数理统计学是一门以概率论为基础，应用性很强的学科。它研究怎样以有效的方式收集、 整理和分析带有随机性的数据，以便对所考察的问题作出正确的推断和预测，为采取正确的决策和行动提供依据和建议。数理统计不同于一般的资料统计，它更侧重于应用随机现象本身的规律性进行资料的收集、整理和分析。

　　【简单的讲】，就是通过样本分析来推断整体。

　　【意义或者重要性】在这个大数据时代，数据是非常重要的。怎样挖掘数据内部的规律或者隐含的信息，变得尤为重要。当时我们是不可能获得整体的数据的，所以我们只能通过抽取样本，进而通过样本来推断整体的规律。

　　【目录】

　　第一章、样本与统计量

　　　　一、引言：

　　　　二、总体与样本：

　　　　三、统计量：

　　　　四、常用分布：

　　第二章、参数估计

　　　　一、引言：

　　　　二、点估计——矩估计法：

　　　　三、点估计——极大似然估计：

　　　　四、估计量的优良性准则

　　　　五、区间估计——正态分布

　　　　　　1、引入

　　　　　　2、单个正态总体参数的区间估计

　　　　　　3、两个正态总体的区间估计

　　　　六、区间估计——非正态分布：

　　　　　　1、大样本正态近似法

　　　　　　2、二项分布

　　　　　　3、泊松分布

　　第三章、假设检验

　　　　一、引言：

　　　　二、正态总体均值的假设检验

　　　　　　1、单正态总体 N(μ, σ²)均值 μ 的检验

　　　　　　　　（1） 双边检验 H₀: μ = μ₀；H₁: μ≠μ₀ 

　　　　　　　　（2） 单边检验 H₀: μ = μ₀；H₁: μ>μ₀

　　　　　　2、两个正态总体 N(μ₁, σ₁²) 和  N(μ₂, σ₂²)均值的比较

　　　　　　　　（1） 双边检验 H₀: μ₁ = μ₂；H₁: μ₁≠μ₂ 

 　　　　　　  　（2） 单边检验 H₀: μ₁ >= μ₂；H₁: μ₁<μ₂ 

　　　　　　　　（3） 单边检验 H₀: μ₁ <= μ₂；H₁: μ₁>μ₂ 

　　　　三、正态总体方差的检验

　　　　　　1、单个正态总体方差的 χ2 检验

　　　　　　　　（1） H₀: σ² =σ₀²；H₁: σ² ≠σ₀²

　　　　　　　　（2） H₀: σ² =σ₀²；H₁: σ² >σ₀²

　　　　　　　　（3)  H₀: σ² ≤σ₀²；H₁: σ² > σ₀² (同2.)

　　　　　　2、两正态总体方差比的 F 检验

　　　　　　　　　(1).  H₀: σ₁² = σ₂²；H₁: σ₁² ≠  σ₂².

　　　　　　　　 （2） H₀: σ₁² = σ₂²；H₁:    σ₁²> σ₂²

　　　　　　　　 （3） H₀: σ₁² ≤ σ₂²；H₁:    σ₁²> σ₂²

 　　第四章、回归分析

　　　　一、引言

　　　　二、一元线性回归

　　　　　　1、一元线性回归模型

　　　　　　2、回归系数的最小二乘估计：

　　　　　　3、回归方程的显著性检验

　　　　　　　　（1）F 检验

　　　　　　　　（2）T 检验

　　　　  　　　 （3）相关系数检验

　　　　　　4、估计与预测

　　　　　　　　（1） E(y₀)的估计

　　　　　　　　（2） y₀的预测区间

 　　　　三、广义线性回归模型

　　　　 四、非线性回归模型

第四章、回归分析

　　一、引言：

　　变量间的两类关系：十九世纪，英国生物学家兼统计学家高尔顿研究发现：

     其中x表示父亲身高， y 表示成年儿子的身高（单位：英寸，1英寸=2.54厘米）。这表明子代的平均高度有向中心回归的意思，使得一段时间内人的身高相对稳定。之后回归分析的思想渗透到了数理统计的其它分支中。

 　  Ø 回归分析处理的是变量与变量间的关系。变量间常见的关系有两类：确定性关系与相关关系。

　   Ø 变量间的相关关系不能用完全确切的函数形式表示，但在平均意义下有一定的定量关系表达式，寻找这种定量关系表达式就是回归分析的主要任务。

  　 Ø 回归分析便是研究变量间相关关系的一门学科。它通过对客观事物中变量的大量观察或试验获得的数据，去寻找隐藏在数据背后的相关关系，给出它们的表达形式——回归函数的估计。

　　

　　二、一元线性回归

　　1、一元线性回归模型

　　设y与x间有相关关系，称x为自变量(预报变量)，y为因变量(响应变量)，在知道x取值后，y有一个分布p(y|x)，我们关心的是y的均值E(Y|x)：

　　　　

　　这便是y关于x的理论回归函数——条件期望，也就是我们要寻找的相关关系的表达式。通常，相关关系可用下式表示：y =f (x)+ ε，其中ε是随机误差，一般假设ε ~N(0,σ²)。

　　进行回归分析首先是回归函数形式的选择。当只有一个自变量时，通常可采用画散点图 的方法进行选择。

　　【例1】合金的强度y (×10⁷Pa) 与合金中碳的含量x (%) 有关。为研究两个变量间的关系。首先是收集数据，我们把收集到的数据记为(x_i,y_i) ,i=1,2, ... , n。本例中，我们收集到12组数据，列于表1中

　　　　

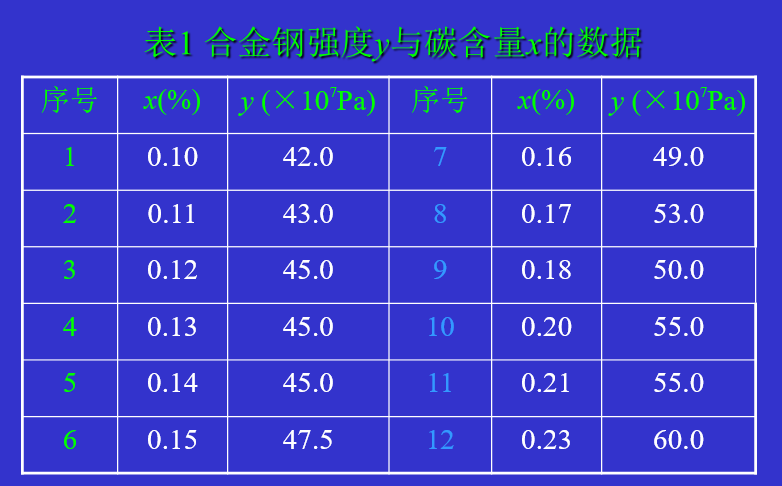
　　为找出两个量间存在的回归函数的形式，可以画一张图：把每一对数(x_i,y_i)看成直角坐标系中的一个点，在图上画出n个点，称这张图为散点图，见图1

　　　　

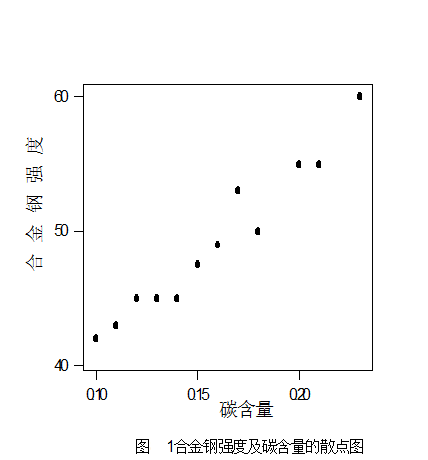
　　从散点图我们发现12个点基本在一条直线附近，这说明两个变量之间有一个线性相关关系，这个相关关系可以表示为

                        y =Β₀+ Β₁x+ ε                                        (2)

    这便是y关于x的一元线性回归的数据结构式。通常假定

                        E(ε) =0,  Var(ε) = σ²                                                      (3)

    在对未知参数作区间估计或假设检验时，还需要假定误差服从正态分布，即

                        y ~N(Β₀+ Β₁x , σ² )                                 (4)

　　显然，假定(4) 比 (3) 要强。

　　由于 Β₀, Β₁均未知，需要我们从收集到的数据(x_i,y_i)，i=1,2,…,n，出发进行估计。在收集数据时，我们一般要求观察独立地进行，即假定y₁, y₂,…, y_n,相互独立。综合上述诸项假定，我们可以给出最简单、常用的一元线性回归的数学模型：

　　　　

　　由数据(x_i,y_i)，i=1,2,…,n，可以获得Β₀, Β₁的估计 ，称

　　　　

　　为y关于x的经验回归函数，简称为回归方程，其图形称为回归直线。给定x=x₀后， 称为回归值（在不同场合也称其为拟合值、预测值）。

　　2、回归系数的最小二乘估计：

　　　　

　　　　

　　　　

　　【例2】使用例1中合金钢强度和碳含量数据，我们可求得回归方程，见下表.

　　　　

　　【性质】关于最小二乘估计的一些性质罗列在如下定理之中

　　　　

　　　　

　　【证明】定理1证明如下：

　　

　　

　　

 　　3、回归方程的显著性检验

　　在使用回归方程作进一步的分析以前，首先应对回归方程是否有意义进行判断。如果Β₁=0，那么不管x如何变化，E(y)不随x的变化作线性变化，那么这时求得的一元线性回归方程就没有意义，称回归方程不显著。如果Β₁≠0，E(y)随x的变化作线性变化，称回归方程是显著的。

    综上，对回归方程是否有意义作判断就是要作如下的显著性检验：H₀：Β₁=0      vs      H₁： Β₁≠0  。拒绝H₀表示回归方程是显著的。

　　在一元线性回归中有三种等价的检验方法，下面分别加以介绍。

　　（1）F 检验:采用方差分析的思想，我们从数据出发研究各y_i不同的原因。

　　

　　【证明】公式（13）证明如下：

　　

　　【推论】

　　

 　　关于S_R 和 S_e所含有的成分可由如下定理说明

　　

　　进一步，有关SR 和 Se的分布，有如下定理。

　　

　　如同方差分析那样，我们可以考虑采用F比作为检验统计量：

　　

　　【例3】在合金钢强度的例2中，我们已求出了回归方程，这里我们考虑关于回归方程的显著性检验。

　　

　　（2）T 检验：

　　对H₀ ： Β₁ =0的检验也可基于t分布进行。

　　

　　

　　

　　（3）相关系数检验

　　一元线性回归方程是反映两个随机变量x与y间的线性相关关系，它的显著性检验还可通过对二维总体相关系数r的检验进行。（相关系数的概念可见【第一章------>三、统计量】）

　　

　　

　　

　　【总结】在一元线性回归场合，三种检验方法是等价的：在相同的显著性水平下，要么都拒绝原假设，要么都接受原假设，不会产生矛盾。  F 检验可以很容易推广到多元回归分析场合，而其他二个则否，所以，F检验是最常用的关于回归方程显著性检验的检验方法。

 　　4、估计与预测：

　　当回归方程经过检验是显著的后，可用来做估计和预测。这是二个不同的问题：

　　

　　（1） E(y₀)的估计

　　在x=x₀时，其对应的因变量y₀是一个随机变量，有一个分布，我们经常需要对该分布的均值给出估计。

　　

　　

　　

　　（2） y₀的预测区间

　　

　　【详细过程】

　　

　　

　　

　　

 　　三、广义线性回归模型

　　 四、非线性回归模型