高等数理统计（五）

引言

　　【比较官方的简介】数理统计学是一门以概率论为基础，应用性很强的学科。它研究怎样以有效的方式收集、 整理和分析带有随机性的数据，以便对所考察的问题作出正确的推断和预测，为采取正确的决策和行动提供依据和建议。数理统计不同于一般的资料统计，它更侧重于应用随机现象本身的规律性进行资料的收集、整理和分析。

　　【简单的讲】，就是通过样本分析来推断整体。

　　【意义或者重要性】在这个大数据时代，数据是非常重要的。怎样挖掘数据内部的规律或者隐含的信息，变得尤为重要。当时我们是不可能获得整体的数据的，所以我们只能通过抽取样本，进而通过样本来推断整体的规律。

　　【目录】

　　第一章、样本与统计量

　　　　一、引言：

　　　　二、总体与样本：

　　　　三、统计量：

　　　　四、常用分布：

　　第二章、参数估计

　　　　一、引言：

　　　　二、点估计——矩估计法：

　　　　三、点估计——极大似然估计：

　　　　四、估计量的优良性准则

　　　　五、区间估计——正态分布

　　　　　　1、引入

　　　　　　2、单个正态总体参数的区间估计

　　　　　　3、两个正态总体的区间估计

　　　　六、区间估计——非正态分布：

　　　　　　1、大样本正态近似法

　　　　　　2、二项分布

　　　　　　3、泊松分布

　　第三章、假设检验

　　　　一、引言：

　　　　二、正态总体均值的假设检验

　　　　　　1、单正态总体 N(μ, σ²)均值 μ 的检验

　　　　　　　　（1） 双边检验 H₀: μ = μ₀；H₁: μ≠μ₀ 

　　　　　　　　（2） 单边检验 H₀: μ = μ₀；H₁: μ>μ₀

　　　　　　2、两个正态总体 N(μ₁, σ₁²) 和  N(μ₂, σ₂²)均值的比较

　　　　　　　　（1） 双边检验 H₀: μ₁ = μ₂；H₁: μ₁≠μ₂ 

 　　　　　　  　（2） 单边检验 H₀: μ₁ >= μ₂；H₁: μ₁<μ₂ 

　　　　　　　　（3） 单边检验 H₀: μ₁ <= μ₂；H₁: μ₁>μ₂ 

　　　　三、正态总体方差的检验

　　　　　　1、单个正态总体方差的 χ2 检验

　　　　　　　　（1） H₀: σ² =σ₀²；H₁: σ² ≠σ₀²

　　　　　　　　（2） H₀: σ² =σ₀²；H₁: σ² >σ₀²

　　　　　　　　（3)  H₀: σ² ≤σ₀²；H₁: σ² > σ₀² (同2.)

　　　　　　2、两正态总体方差比的 F 检验

　　　　　　　　　(1).  H₀: σ₁² = σ₂²；H₁: σ₁² ≠  σ₂².

　　　　　　　　 （2） H₀: σ₁² = σ₂²；H₁:    σ₁²> σ₂²

　　　　　　　　 （3） H₀: σ₁² ≤ σ₂²；H₁:    σ₁²> σ₂²

 　　第四章、回归分析

　　　　一、引言

　　　　二、一元线性回归

　　　　　　1、一元线性回归模型

　　　　　　2、回归系数的最小二乘估计：

　　　　　　3、回归方程的显著性检验

　　　　　　　　（1）F 检验

　　　　　　　　（2）T 检验

　　　　  　　　 （3）相关系数检验

　　　　　　4、估计与预测

　　　　　　　　（1） E(y₀)的估计

　　　　　　　　（2） y₀的预测区间

 　　　　三、广义线性回归模型

　　　　 四、非线性回归模型

 　　第五章、方差分析

　　　　一、引言

　　　　二、单因子方差分析的统计模型  

　　　　三、平方和分解

　　　　四、参数估计

　　　　　　1、点估计：正态分布的极大似然估计

　　　　　　2、置信区间

　　　　五、重复数不等情形

　　　　六、多重比较

　　　　　　1、效应差的置信区间

　　　　　　2、之后补充

　　　　

　　　　七、方差齐性检验

　　　　　　1、Hartley检验

　　　　　　

第五章、方差分析

　　一、引言：

　　方差分析是研究一种或多种因素的变化对试验结果的观测值是否有显著影响，从而找出较优的试验条件或生产条件的一种常用数理统计方法。

　　【方差分析的另外一种提法】实际工作中我们经常碰到多个正态总体均值的比较问题，处理这类问题通常采用所谓的方差分析方法；即不同因素水平产生多个正态分布，方差分析就是这多个正态分布进行分析。 

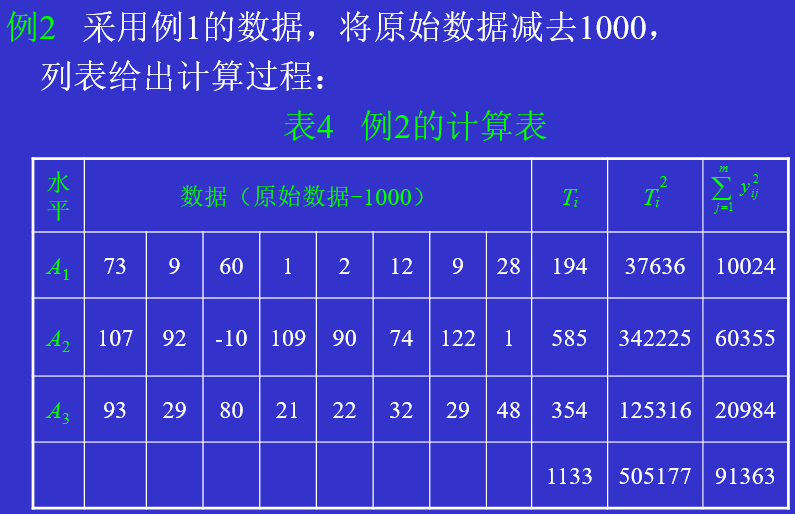
　　【例1】在饲料养鸡增肥的研究中，某研究所提出三种饲料配方：A₁是以鱼粉为主的饲料，A₂是以槐树粉为主的饲料，A₃是以苜蓿粉为主的饲料。为比较三种饲料的效果，特选 24 只相似的雏鸡随机均分为三组，每组各喂一种饲料，60天后观察它们的重量。试验结果如下表所示：  

　　

    本例中，我们要比较的是三种饲料对鸡的增肥作用是否相同。为此，把饲料称为因子，记为A，三种不同的配方称为因子A的三个水平，记为A₁, A₂, A₃，使用配方A_i下第 j 只鸡60天后的重量用y_ij表示，i=1, 2, 3,  j=1, 2,..., 10。我们的目的是比较三种饲料配方下鸡的平均重量是否相等，为此，需要做一些基本假定，把所研究的问题归结为一个统计问题，然后用方差分析的方法进行解决。

　　二、单因子方差分析的统计模型 :

    在例1中我们只考察了一个因子，称其为单因子试验。

    通常，在单因子试验中，记因子为 A, 设其有r个水平，记为A₁, A₂,…, A_r，在每一水平下考察的指标可以看成一个总体 ，现有 r 个水平，故有 r 个总体， 假定：

　　1)每一总体均为正态总体，记为 N(μ_i ,σ_i²)，      i＝1, 2,…, r ；

　　2)各总体的方差相同:  σ₁²=σ₂²=…=σ_r² =σ² ；

　　3)从每一总体中抽取的样本是相互独立的， 即所有的试验结果 y_ij 都相互独立。  

　　我们要比较各水平下的均值是否相同,

     即要对如下的一个假设进行检验:  H₀ ：μ₁ =μ₂ =…=μ_r                      （1）

    　　　　　　　　　 备择假设为  H₁ ：μ₁, μ₂, …, μ_r 不全相等

    在不会引起误解的情况下， H₁ 通常可省略不写。

    如果H₀成立，因子A的r个水平均值相同，称因子A的r个水平间没有显著差异，简称因子A不显著；反之，当H₀不成立时，因子A的r个水平均值不全相同，这时称因子A的不同水平间有显著差异，简称因子A显著。

　　为对假设（1）进行检验，需要从每一水平下的总体抽取样本，设从第i个水平下的总体获得m个试验结果，记 y_ij 表示第i个总体的第j次重复试验结果。共得如下n=r×m个试验结果：

y_ij， i＝1, 2,…, r ， j＝1, 2, …, m, 其中r为水平数，m为重复数，i为水平编号，j 为重复编号。

　　在水平Ai下的试验结果y_ij与该水平下的指标均值 μ_i  一般总是有差距的，记 ε_ij = y_ij-μ_i，e_ij  称为随机误差。于是有：y_ij = μ_i +ε_ij               （2）

  （2）式称为试验结果 y_ij 的数据结构式。

　　【单因子方差分析的统计模型】

　　

 　　

　　三、平方和分解：

　　1、通常在单因子方差分析中可将试验数据列成如下表格形式：

　　

　　

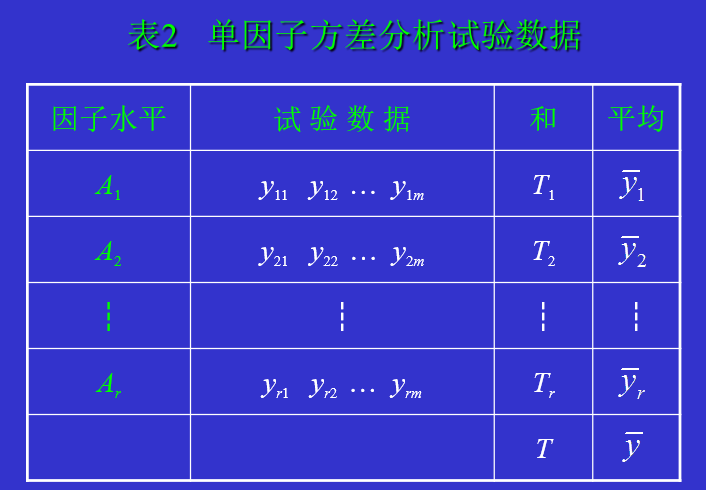
　　2、组内偏差与组间偏差：

　　

　　

　　3、偏差平方和及其自由度：

 　　

【重要】偏差平方和与自由度的关系，接下来三个自由度都可由此推出！

　　

　　4、总平方和分解公式

　　

　　组内偏差平方和自由度计算如下：每组的自由度都为（m-1），则总共r组，所以总自由度为 （m-1）*r = m*r -r = n-r

 　　

　　

　　5、检验方法

　　

　　

　　

　　

　　

　　

　　

　　

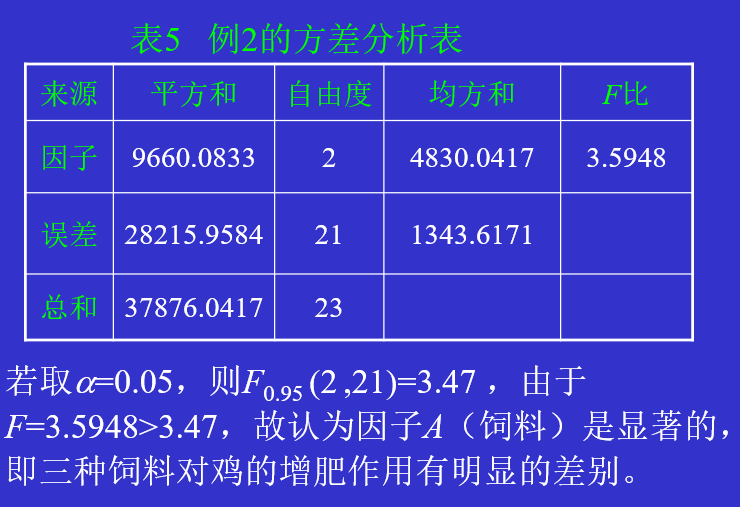
四、参数估计

　　在检验结果为显著时，我们可进一步求出总均值μ 、各主效应a_i和误差方差σ²的估计

　　1、点估计：正态分布的极大似然估计

　　

　　因为 E（S_e）= σ² * （n-r） ；所以 E（S_e/n）= σ² * （n-r）/n ≠ σ² ，所以不满足无偏性，更具体关于无偏性，可查看【第二章、参数估计-四、估计量的优良性准则】

　　2、置信区间

　　

　　红框部分证明如下：根据【第一章、样本与统计量-中心极限定理】证明如下：

　　

　　 　　

　　

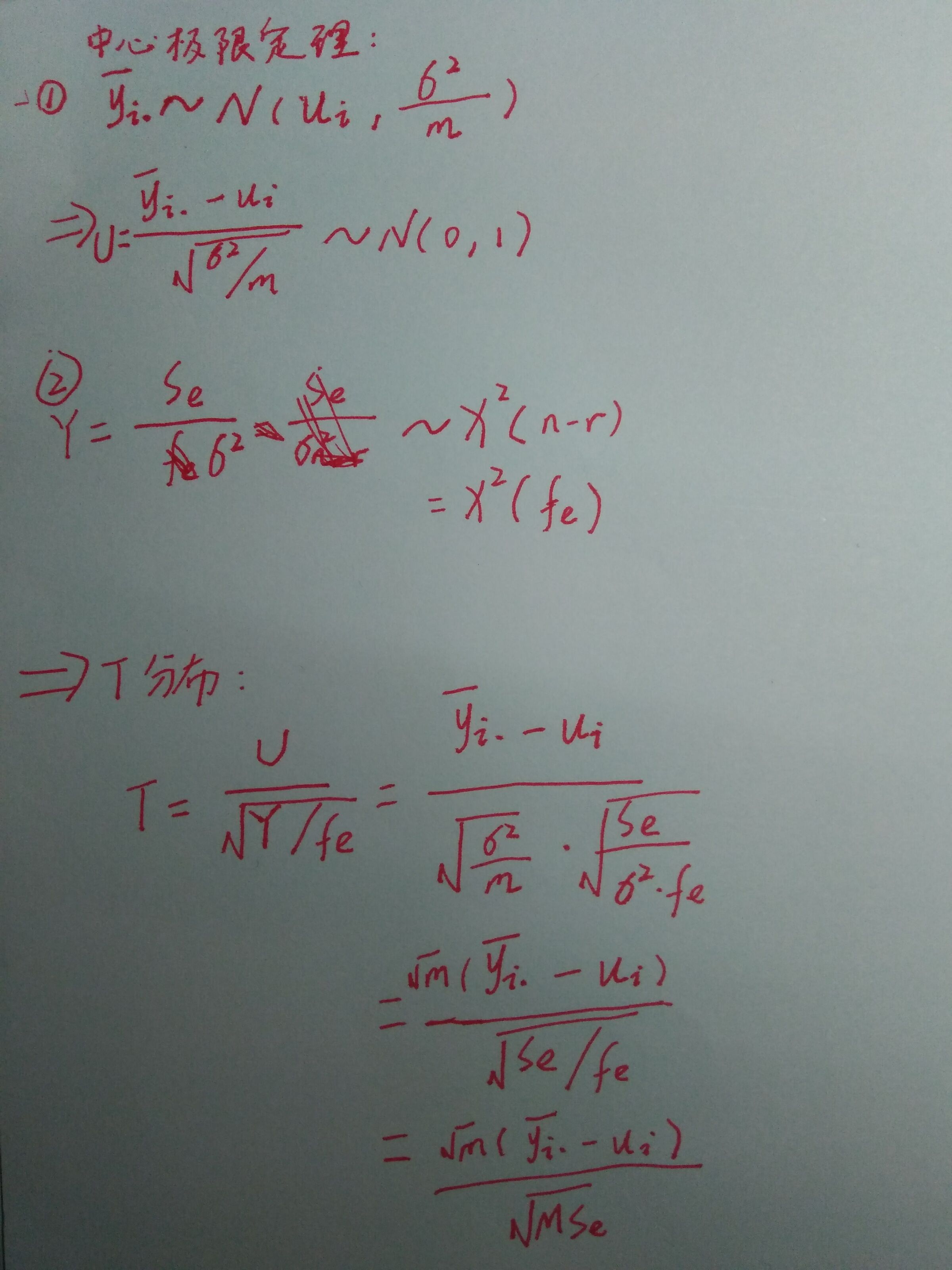
　　【总结】在单因子试验的数据分析中可得到如下三个结果：

　　　　Ø 因子是否显著；

　　　　Ø 试验的误差方差σ²的估计；

　　　　Ø 诸水平均值μ_i的点估计与区间估计。

　　在因子A显著时，通常只需对较优的水平均值作参数估计，在因子A不显著场合，参数估计无需进行。

五、重复数不等情形

　　单因子方差分析并不要求每个水平下重复试验次数全相等，在重复数不等场合的方差分析与重复数相等情况下的方差分析极为相似，只在几处略有差别。

　　

　　

　　

　　

　　

　　

　　

　　

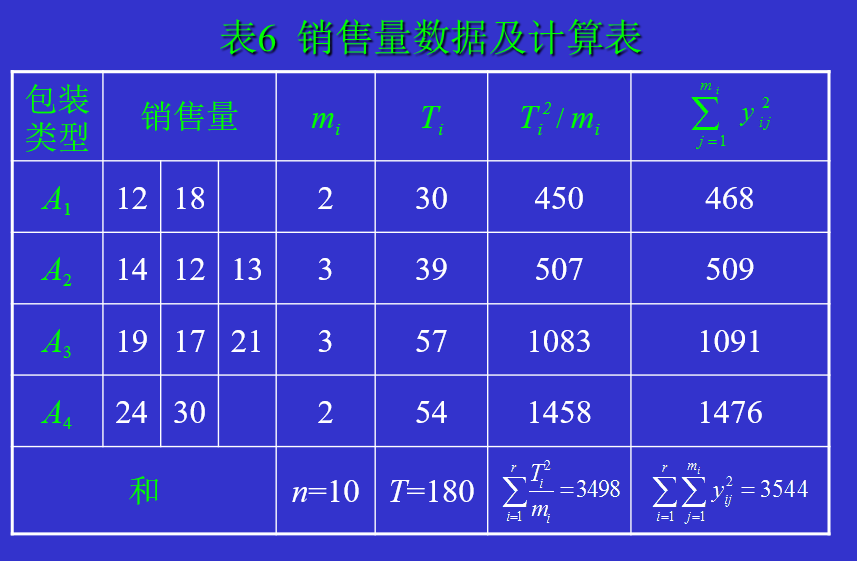
六、多重比较

　　1、效应差的置信区间：

　　如果方差分析的结果因子A显著，则等于说有充分理由认为因子A各水平的效应不全相同，但这并不是说它们中一定没有相同的。就指定的一对水平A_i与A_j，我们可通过求μ_i - μ_j的区间估计来进行比较。

　　

　　这里的置信区间与两样本的t区间基本一致，区别在于这里σ²的估计使用了全部样本而不仅仅是两个水平A_i, A_j下的观测值。

　　

　　2、多重比较问题

七、方差齐性检验

　　1、Hartley检验

　　在进行方差分析时要求r个方差相等，这称为方差齐性。理论研究表明，当正态性假定不满足时对F检验影响较小,即F检验对正态性的偏离具有一定的稳健性，而F检验对方差齐性的偏离较为敏感。所以r个方差的齐性检验就显得十分必要。

    所谓方差齐性检验是对如下一对假设作出检验：

　　

　　很多统计学家提出了一些很好的检验方法，这里介绍几个最常用的检验，它们是：

　　Ø Hartley检验，仅适用于样本量相等的场合；

　　Ø Bartlett检验，可用于样本量相等或不等的场合，但是每个样本量不得低于5；

　　Ø 修正的Bartlett检验，在样本量较小或较大、相等或不等场合均可使用。