计算两张黑白图片的相似度

如果有两张分辨率为32x32的黑白图片，要计算这两张图片的相似度该怎么办？

根据这篇文章《数学之美 系列 12 - 余弦定理和新闻的分类》的介绍，我们只需要计算一下两个1024位(32x32=1024)的向量之间的夹角的余弦即可，结果越接近于1，相似度就越高。

好了，理论基础有了，下面说怎么存储我们的向量。

因为图片上只有两种颜色，所以用1位二进制足以表示。那就认为白色的点为0，黑色的点为1。这样，我们每一张图片就可以放在32个32位整数里，每行用一个整数表示，既节省了空间，又降低了操作时的复杂度。

接下来说如何计算。

如果老老实实的按照以下公式进行计算，我们需要取出整数中相应位的值，然后相乘或者分别平方，显然这种方法很浪费时间。

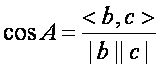
我们来看看有没有什么简便方法。

因为我们只有0或者1两种值，所以，分子中的相应位分别相乘，就可以转化为相应位进行与运算，又因为我们使用了整型存储，所以计算进一步简化为两个整数按位与。

而分母中的按位分别平方然后相加，就可以省掉平方的操作，直接按位相加了。

因此，整个程序的操作过程就可以按照如下步骤进行：

1.将每张图片按像素存放到一个长度为32的32位整型数组里面，每个整数存放一行，整数的每位存放一个像素值（0或者1）；

2.计算分子时，将两个这样的数组中的整数按照对应的索引分别按位与，然后将计算结果按位相加；

3.计算分母时，将每个数组中的所有整数按位相加，然后开根号，最后相乘；

4.分子除以分母，得出余弦值。

第2、3、4步的代码如下：

public double GetCosine(int[] e1, int[] e2)
{
    int a = 0;//分母1
    int b = 0;//分母2
    int c = 0;//分子
    for (int y = 0; y < 32; ++y)
    {
        //两个数组中的整数按位与
        int i = e2[y] & e1[y];
        //按位加
        for (int x = 1; x < 33; ++x)
        {
            c += (i >> x) & 1;
            a += (e2[y] >> x) & 1;
            b += (e1[y] >> x) & 1;
        }
    }

    //计算分母
    int d = a * b;

    return d == 0 ? 0 : c / Math.Sqrt(d);
}

如果看到了这里，你已经知道了我们该如何计算两个图片的相似度，按我的经验，计算结果超过0.8，就可以认为这两个图片一样了。

如果把这里的图片换成验证码，而你碰巧已经知道其中一个验证码的值，那么另外一个验证码的值你现在也知道了。