【2021.02.17】线性模型、梯度下降算法

【2021.02.17】线性模型、梯度下降算法

本期的学习来源是：https://www.bilibili.com/video/BV1Y7411d7Ys?p=2

准备数据集->进行模型选择或者模型设计->训练模型->应用/推理

过拟合：机器学习学到了噪声

泛化：对未识别的图案进行分类

模型设计

找到最适合数据集的模型

先用线性模型进行测试

其中线性模型的函数那个y被叫做y_hat

在开始进行测试前要先简化模型，如下式就先简化掉截距

使用随机值开始，然后进行评估（看偏移程度有多大）

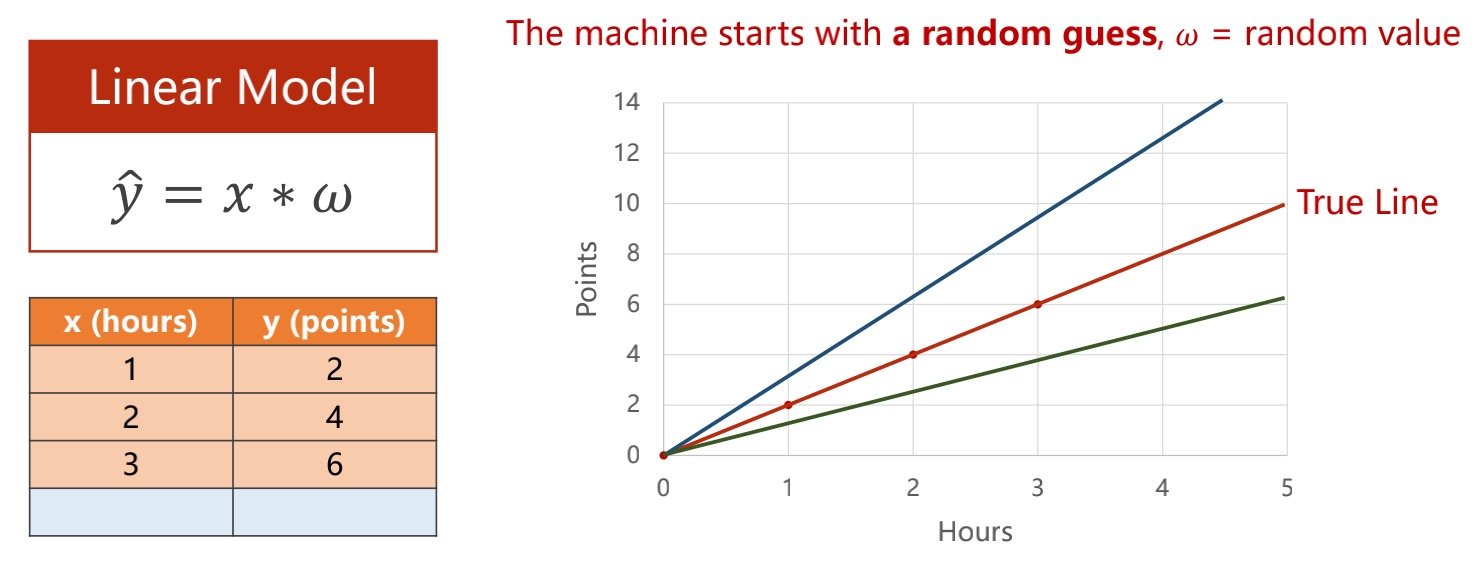
评估模型在机器学习中被称为损失函数

损失函数是针对其中一个样本的，结果要算出平均的误差（例如各个样本的损失函数之和平均）

针对上方表格的数据，下图将value值/权重值设定为3（随机权重类似于穷举法）

算出预测值（第三列），算出损失（第四列），并得出平均损失（越小越好）

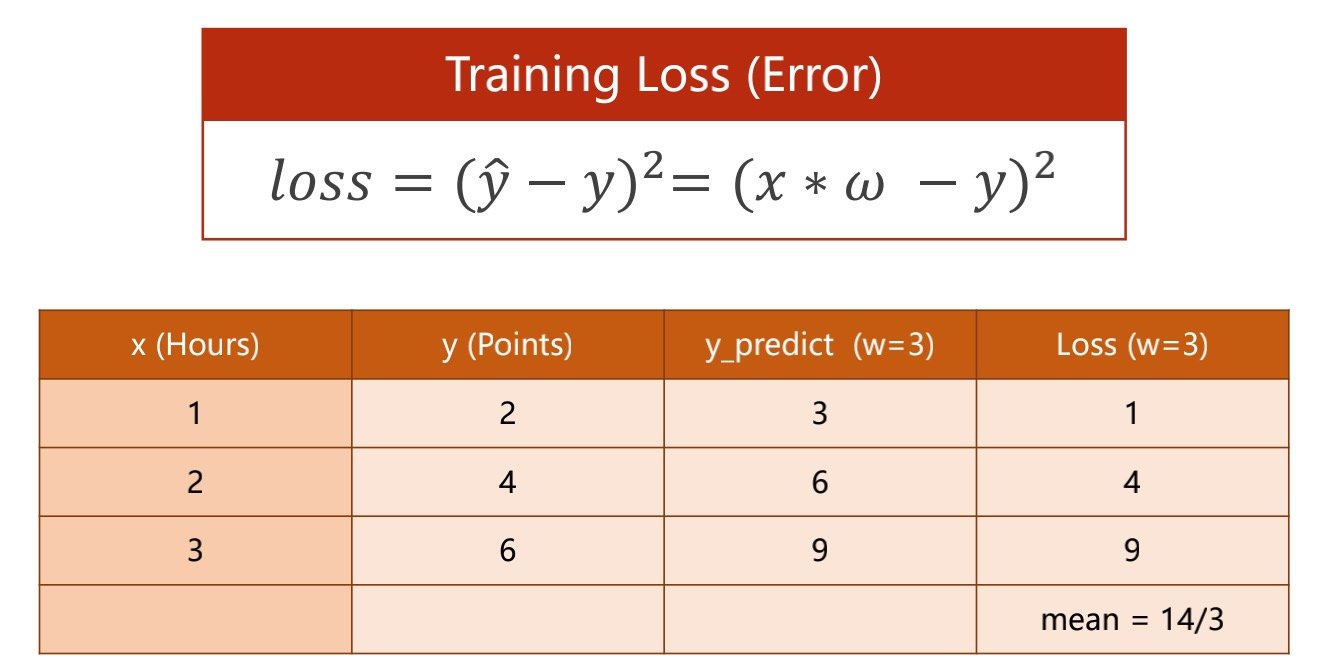
损失函数有很多种类，这种计算方差的方法是其中一种

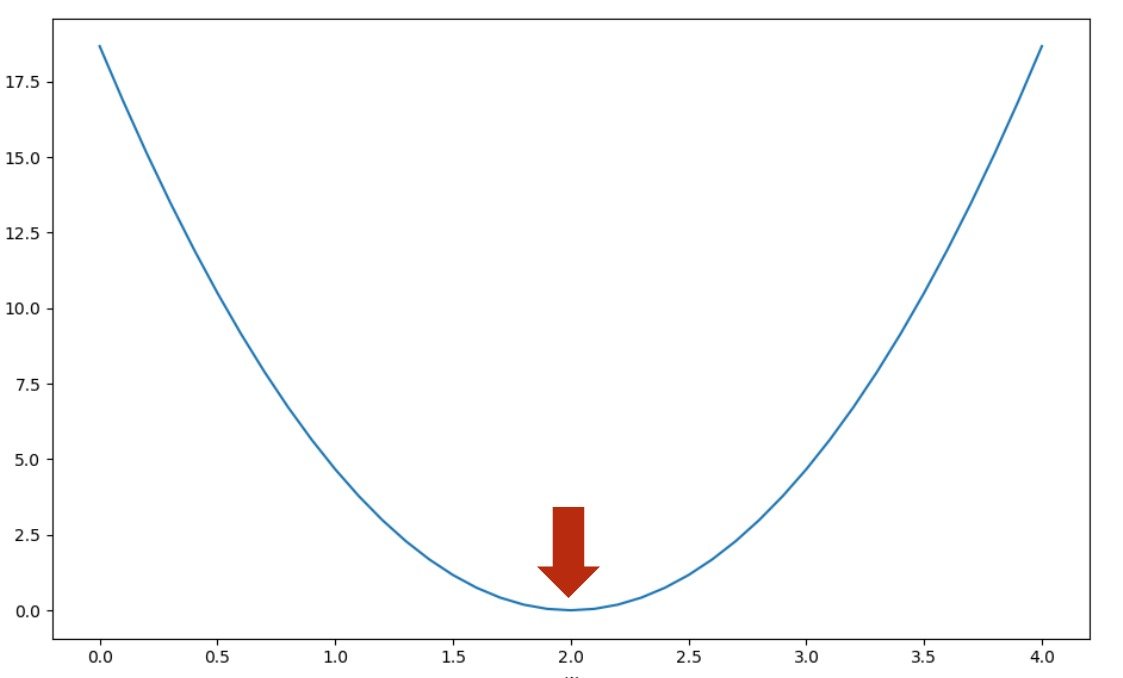
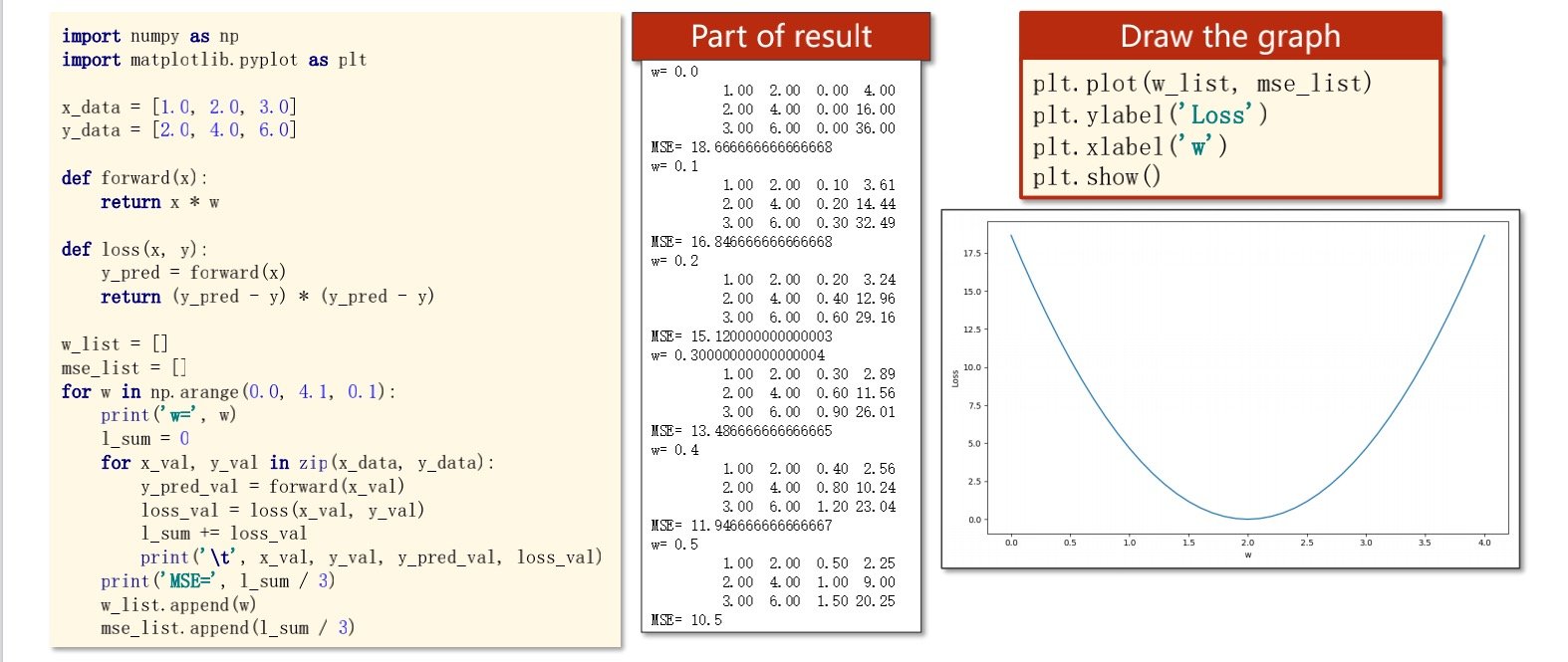
怎样画出损失函数图形

例如下图

#!/usr/bin/env python
# coding: utf-8

# In[1]:


import numpy as np
import matplotlib.pyplot as plt
 
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
 
# 前向传播
def forward(x):
    return x*w
 
# 单个样本的损失函数
def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y)**2


# In[5]:


# 穷举法
# 这里的W是权重
w_list = []
# MSE是均方误差的意思
mse_list = []
# 从零开始，到4.1，间隔0.1取一个样本
for w in np.arange(0.0, 4.1, 0.1):
    print("w=", w)
    l_sum = 0
    for x_val, y_val in zip(x_data, y_data):
        y_pred_val = forward(x_val)
        loss_val = loss(x_val, y_val)
        l_sum += loss_val
        print('	', x_val, y_val, y_pred_val, loss_val)
    print('MSE=', l_sum/3 , '
')
    w_list.append(w)
    mse_list.append(l_sum/3)


# In[4]:


# 导入数组数据
plt.plot(w_list,mse_list)
# 横纵轴的命名
plt.ylabel('Loss')
plt.xlabel('w')
# 打印
plt.show() 

放在jupyter中运行试一下

输出基本数据是成功的

画出损失函数，其中最低点所得的就是最适合的权重值

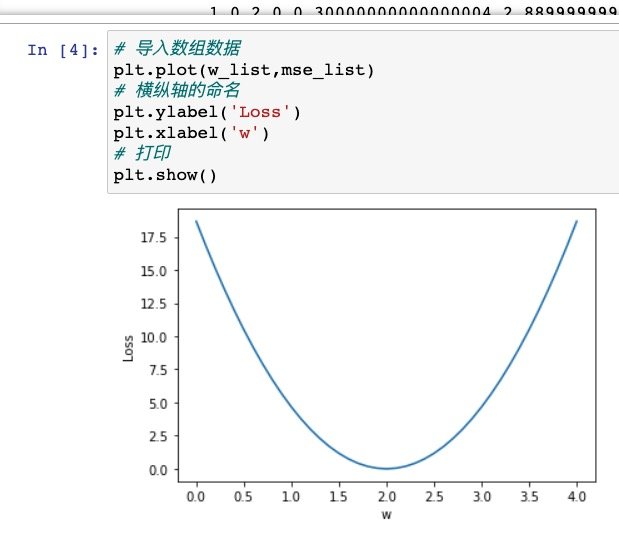
如果是在现实情况中

对同一训练集会慢慢收敛（绿色线），但是在实际开发中会有过拟合，导致在实际情况中不减反增

可使用visdom进行模型可视化，并做好存盘

梯度下降算法

采用了分治的算法，先分散进行穷举，对较好的权重值范围进行穷举

但是损失函数的曲线不够光滑的话，会导致局部最优的情况发生

例如在下图中找到的四个点中，最低点的附近并不能帮助我们找到权重的最优值

在选择初试权重后，我们要如何调整权重值就成了问题

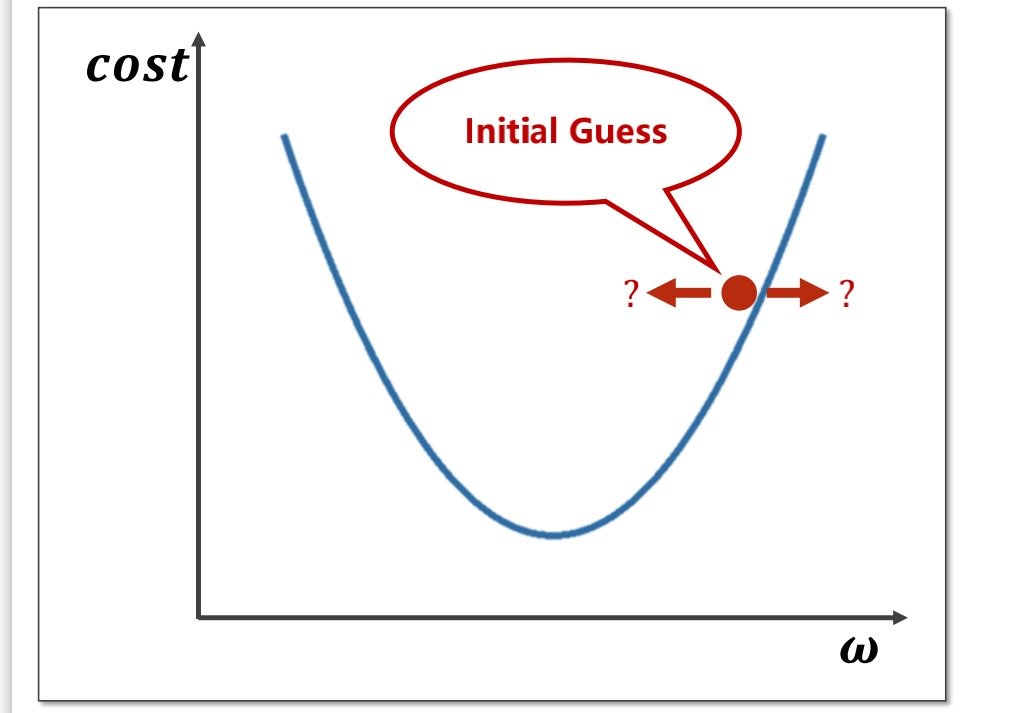
由此我们可以得到更新权重的函数

其中更新权重的函数中的阿尔法值得是学习率

学习率是指更新后迈的步子的大小（学习率过大可能会使得图中小球直接滚到左边的斜坡上

这里体现的算法是“贪心”，我们不一定能得到全局最优的权重，但是可以得到局部最优的权重值

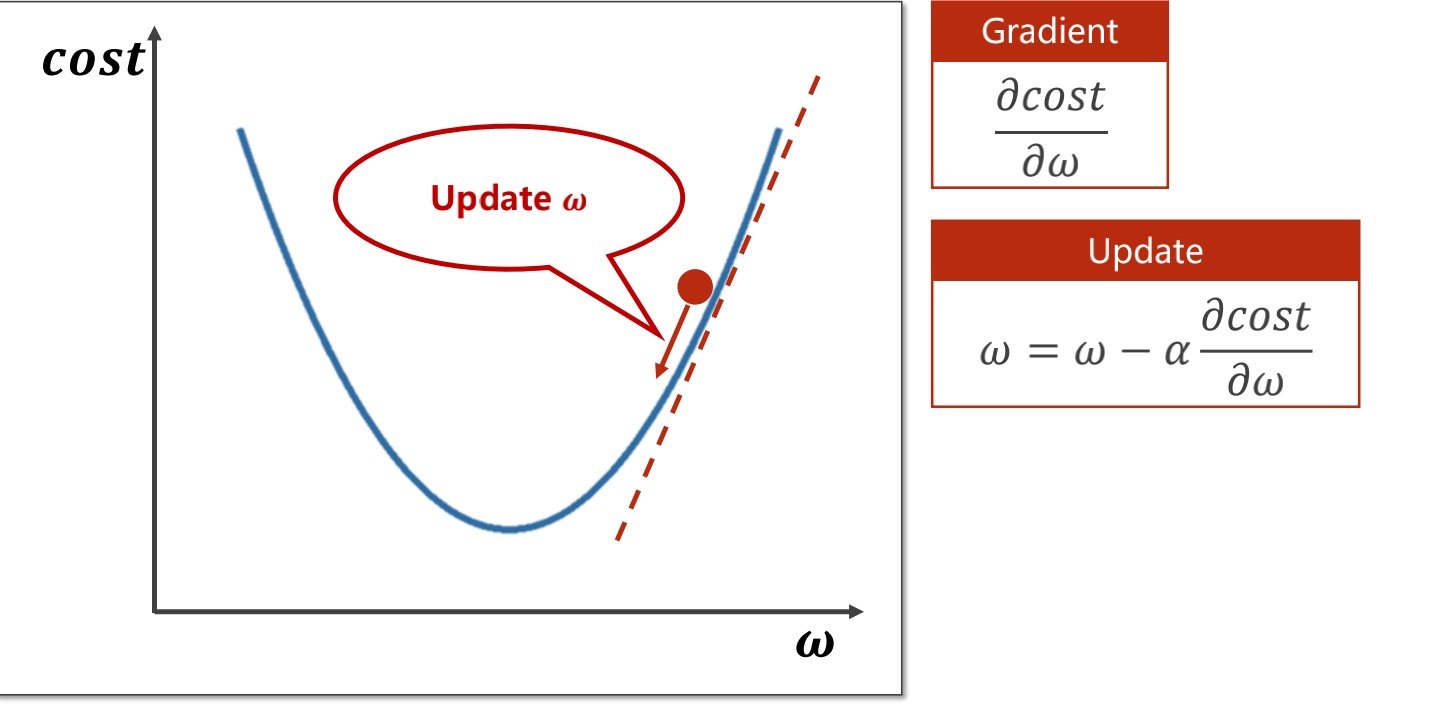
且存在鞍点这种特殊情况

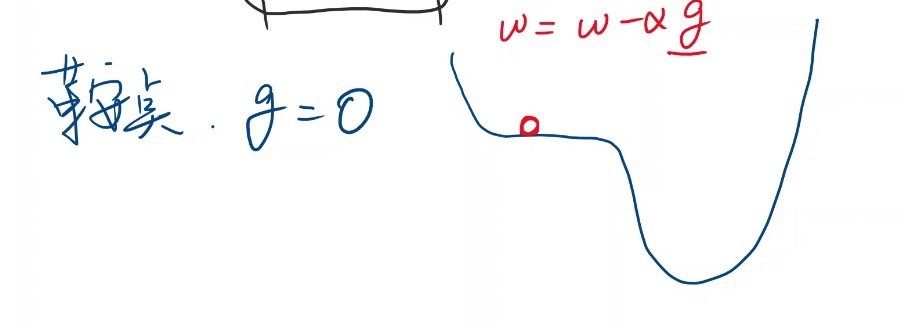
此时权重更新函数并不会使得权重变化

梯度下降法

样例

# 这里是梯度下降法，命名为cost，着眼于整体的损失函数
# 后续还有随机梯度下降法，命名为loss，着眼于选择部分几个样本的损失函数
import matplotlib.pyplot as plt
 
# prepare the training set 样本值
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
 
# initial guess of weight 初始猜测值
w = 1.0
 
# define the model linear model y = w*x 线性模型
def forward(x):
    return x*w
 
#define the cost function MSE 得到方差平均值
def cost(xs, ys):
    cost = 0
    for x, y in zip(xs,ys):
        y_pred = forward(x)
        cost += (y_pred - y)**2
    return cost / len(xs)
 
# define the gradient function  得到梯度函数
def gradient(xs,ys):
    grad = 0
    for x, y in zip(xs,ys):
        grad += 2*x*(x*w - y)
    return grad / len(xs)
 
epoch_list = [] # 训练次数
cost_list = [] # 每个样本的损失函数
print('predict (before training)', 4, forward(4))
for epoch in range(100):
    cost_val = cost(x_data, y_data)
    grad_val = gradient(x_data, y_data)
    w-= 0.01 * grad_val  # 0.01 learning rate 学习率，步进
    print('epoch:', epoch, 'w=', w, 'loss=', cost_val)
    epoch_list.append(epoch)
    cost_list.append(cost_val)
 
print('predict (after training)', 4, forward(4))
plt.plot(epoch_list,cost_list)
plt.ylabel('cost')
plt.xlabel('epoch')
plt.show() 

# python的 for in zip 遍历样例
list_1 = [1, 2, 3, 4]
list_2 = ['a', 'b', 'c']
for x, y in zip(list_1, list_2):
    print(x, y)
    
'''
1 a
2 b
3 c
'''

损失函数反增的情况

在现实情况中，损失函数不一定完全收敛，有可能会出现下方这种反增的情况

这时候最大的可能是学习率过大的原因导致的，迈的步子太大了

随机梯度下降法

随机梯度下降可以帮助我们跨过鞍点

梯度下降法和随机梯度下降法的对比

对比一：

因为梯度下降法取得的是平均值，所以相当于只采用了一个样本，导致损失函数在鞍点的时候无法进行更新权重

而采用随机梯度下降法的时候，是有可能推动损失函数更新的

对比二：

梯度下降法是对每一个点进行单独计算，取的是平均值，因此是可以进行并行计算的

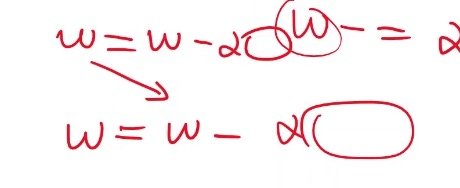
随机梯度下降法存在的缺点是权重更新函数，其中的权重值来自于上一次的权重更新函数的结果

因此随机梯度下降法是串行的，依赖于上一次的权重值更新

批量随机梯度下降（batch）

完整的名字是mini-batch

将数据集作为一个整体进行运算，性能复杂度是低的，时间复杂度也是低的

但是将数据集分割成小块进行运算，性能复杂度是高的，时间复杂度是高的

其中性能复杂度越高越好，时间复杂度越低越好

全部一起性能不好，全都分开对时间复杂度不好

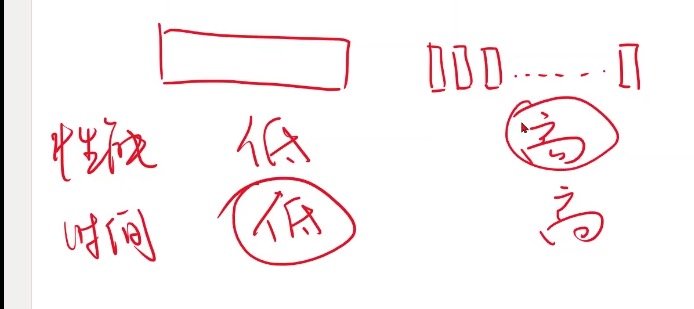
因此要在性能复杂度和时间复杂度上取一个折中

即批量随机梯度下降