zoukankan      html  css  js  c++  java

  • leetcode常规算法题复盘（第九期）——拼接最大数

    题目原文

    321. 拼接最大数

    给定长度分别为 m 和 n 的两个数组，其元素由 0-9 构成，表示两个自然数各位上的数字。现在从这两个数组中选出 k (k <= m + n) 个数字拼接成一个新的数，要求从同一个数组中取出的数字保持其在原数组中的相对顺序。

    求满足该条件的最大数。结果返回一个表示该最大数的长度为 k 的数组。

    说明: 请尽可能地优化你算法的时间和空间复杂度。

    示例 1:

    输入:
nums1 = [3, 4, 6, 5]
nums2 = [9, 1, 2, 5, 8, 3]
k = 5
输出:
[9, 8, 6, 5, 3]

    示例 2:

    输入:
nums1 = [6, 7]
nums2 = [6, 0, 4]
k = 5
输出:
[6, 7, 6, 0, 4]

    示例 3:

    输入:
nums1 = [3, 9]
nums2 = [8, 9]
k = 3
输出:
[9, 8, 9]

    尝试解答

    在玩花活失败后老老实实分两部完成算法，自己的代码如下：

      1 class Solution:
  2     def maxNumber(self,nums1, nums2, k):
  3         m = len(nums1)
  4         n = len(nums2)
  5         if n<k:
  6             x = k-n
  7         else:
  8             x = 0
  9         res = [0]*k
 10         while(x<=k and x<=m):
 11             max_nums1 = self.findMaxList(nums1,x)
 12             #print(max_nums1)
 13             max_nums2 = self.findMaxList(nums2,k-x)
 14             #print(max_nums2)
 15             cur = self.purgeList(max_nums1,max_nums2)
 16             #print("cur")
 17             #print(cur)
 18             res = self.compareList(cur,res)
 19             #print(res)
 20             x += 1
 21         return res
 22 
 23     def findMaxList(self,nums,x):
 24         stack = []
 25         result = nums[:x]
 26         #print("000")
 27         #print(result)
 28         for i in range(0,len(nums)):
 29             if (not stack) or (stack[-1]>=nums[i] and len(stack)<x):
 30                 stack.append(nums[i])
 31                 #print(stack)
 32                 if len(stack)==x:
 33                     #print("bbb")
 34                     result = list(stack)
 35                     #print("aaa")
 36                     #print(result)
 37             else:
 38                 while len(stack)>0 and (nums[i]>stack[-1]) and (len(nums)-i>x-len(stack)):
 39                     #print(len(nums)-i)
 40                     #print(x-len(stack))
 41                     stack.pop(-1)
 42                     #print(stack)
 43                 if len(stack)<x:
 44                     stack.append(nums[i])
 45                     #print(stack)
 46                     if len(stack)==x:
 47                         #print("aaa")
 48                         result = list(stack)
 49                         #print("bbb")
 50                         #print(result)
 51         return result
 52                 
 53                 
 54                 
 55     def purgeList(self,nums1,nums2):
 56         result = []
 57         while len(nums1)+len(nums2)>0:
 58             if len(nums1)==0:
 59                 result.extend(nums2)
 60                 break
 61             if len(nums2)==0:
 62                 result.extend(nums1)
 63                 break
 64             else:
 65                 if nums1[0]> nums2[0]:
 66                     result.append(nums1[0])
 67                     nums1 = nums1[1:]
 68                 elif nums1[0]< nums2[0]:
 69                     result.append(nums2[0])
 70                     nums2 = nums2[1:]
 71                 else:
 72                     nn = 1
 73                     _nums1 = nums1[:]
 74                     _nums2 = nums2[:]
 75                     while True:
 76                         if not _nums1[nn:] and _nums2[nn:]:
 77                             result.append(nums2[0])
 78                             nums2 = nums2[1:]
 79                             break
 80                         if _nums1[nn:] and not _nums2[nn:]:
 81                             result.append(nums1[0])
 82                             nums1 = nums1[1:]
 83                             break
 84                         if _nums1[nn:] and _nums2[nn:]:
 85                             if _nums1[nn:][0]>_nums2[nn:][0]:
 86                                 result.append(nums1[0])
 87                                 nums1 = nums1[1:]
 88                                 break
 89                             if _nums1[nn:][0]<_nums2[nn:][0]:
 90                                 result.append(nums2[0])
 91                                 nums2 = nums2[1:]
 92                                 break
 93                             else:
 94                                 nn += 1
 95                         else:
 96                             result.append(nums2[0])
 97                             nums2 = nums2[1:]
 98                             break
 99                             
100         return result
101 
102     def compareList(self,cur,res):
103         #print("cur,res")
104         #print(cur)
105         #print(res)
106         lenth = len(cur)
107         i = 0
108         while i<lenth:
109             if cur[i]>res[i]:
110                 return cur
111             if cur[i]<res[i]:
112                 return res
113             else:
114                 i += 1
115         return res

    标准题解

    什么是单调栈？

        要解答本题，我们要借助一种数据结构——单调栈。首先我们要知道什么是单调栈？OI Wiki中给出了详细的介绍以及实现代码，不了解的同学可以点击链接学习一下。
        单调栈的核心代码如下

    （when insert x）：
    insert x
    while (!sta.empty() && sta.top()<x)
        sta.pop()
    sta.push(x)

        简单来说，单调栈就是一个内部元素有序的栈（大->小 or 小->大），可以把它理解为：选择一些元素丢弃，剩下的就是一个单调栈。下图就是一个降序单调栈，也是本题需要用到的单调栈类型；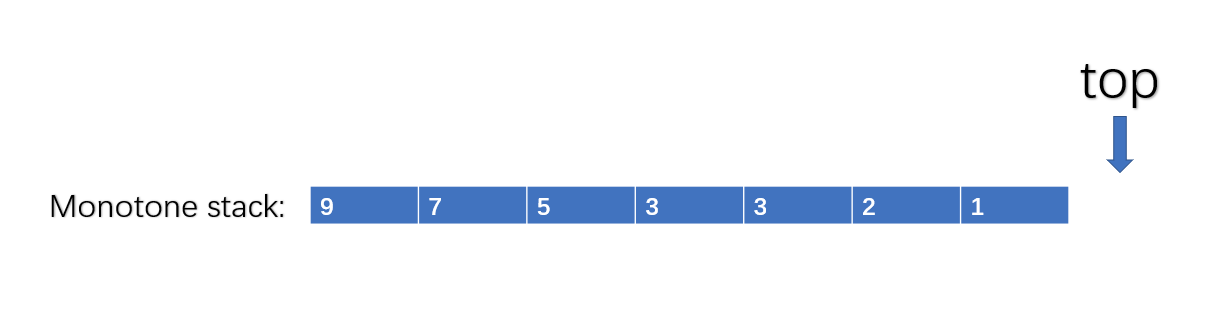

    为什么能使用单调栈？

        本题其实是一道贪心算法题，在两个数组中按序找最大组合，它的最优子结构就是在每个数组中都按序找到最大组合。所以我们可以从每个数组的局部最优，推到全局最优。所以能使用单调栈。

    为什么要使用单调栈？

        这个问题是解决本题的关键，为什么要使用单调栈呢？本题要解决的问题简单来说就是在保证两个输入数组有序的前提下，找到一个最大的组合数。
        所以我们要做的主要有两点：

        保证数组有序的前提下，找到每个数组最大的组合；
        保证两个数组有序的前提下，找到它们的最大拼接；

        单调栈的特性，使得它能轻松地处理第一点。

    这个单调栈不一般！

        哪里不一般？显然是栈内元素数量，普通的单调栈无论是正序或是逆序，都是保证单调栈内元素全部有序，但是本题却不需要保证全部，为什么？答案很简单，我们给定的数量K是确定的，同时我们在循环遍历数组1，2时，每个数组要返回的vector大小也是固定的。所以当我们的单调栈只满足单调性时，元素数很可能不够！这时，我们就需要一些其他操作；
        我们定义了一个遍历drop_num，这个是我们可以丢弃的元素数，一旦drop_num<=0之后，后面的元素都不润许我们丢弃了，简单来说就是返回的单调栈前面是有序的，后面可能无序（直接拼接）。
        举个例子，假如我们给定的数组是【9，10，7，8，4，5，6】，我们要返回的数组大小是5，步骤如下图：

        当我们丢弃了9，8 两个数之后，再丢弃元素就不够了，所以后面的都直接加入栈。

    作者：treasure_
    链接：https://leetcode-cn.com/problems/create-maximum-number/solution/tu-jie-suan-fa-zhe-ge-dan-diao-zhan-bu-yi-ban-by-t/
    来源：力扣（LeetCode）
    著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

     上大佬的代码：

    python

     1 class Solution:
 2     def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:
 3         m, n = len(nums1), len(nums2)
 4         maxSubsequence = [0] * k
 5         start, end = max(0, k - n), min(k, m)
 6 
 7         for i in range(start, end + 1):
 8             subsequence1 = self.getMaxSubsequence(nums1, i)
 9             subsequence2 = self.getMaxSubsequence(nums2, k - i)
10             curMaxSubsequence = self.merge(subsequence1, subsequence2)
11             if self.compare(curMaxSubsequence, 0, maxSubsequence, 0) > 0:
12                 maxSubsequence = curMaxSubsequence
13         
14         return maxSubsequence
15 
16     def getMaxSubsequence(self, nums: List[int], k: int) -> int:
17         stack = [0] * k
18         top = -1
19         remain = len(nums) - k
20 
21         for i, num in enumerate(nums):
22             while top >= 0 and stack[top] < num and remain > 0:
23                 top -= 1
24                 remain -= 1
25             if top < k - 1:
26                 top += 1
27                 stack[top] = num
28             else:
29                 remain -= 1
30         
31         return stack
32 
33     def merge(self, subsequence1: List[int], subsequence2: List[int]) -> List[int]:
34         x, y = len(subsequence1), len(subsequence2)
35         if x == 0:
36             return subsequence2
37         if y == 0:
38             return subsequence1
39         
40         mergeLength = x + y
41         merged = list()
42         index1 = index2 = 0
43 
44         for _ in range(mergeLength):
45             if self.compare(subsequence1, index1, subsequence2, index2) > 0:
46                 merged.append(subsequence1[index1])
47                 index1 += 1
48             else:
49                 merged.append(subsequence2[index2])
50                 index2 += 1
51         
52         return merged
53 
54     def compare(self, subsequence1: List[int], index1: int, subsequence2: List[int], index2: int) -> int:
55         x, y = len(subsequence1), len(subsequence2)
56         while index1 < x and index2 < y:
57             difference = subsequence1[index1] - subsequence2[index2]
58             if difference != 0:
59                 return difference
60             index1 += 1
61             index2 += 1
62         
63         return (x - index1) - (y - index2)
64 
65 
66 #作者：LeetCode-Solution
67 #链接：https://leetcode-cn.com/problems/create-maximum-number/solution/pin-jie-zui-da-shu-by-leetcode-solution/
68 #来源：力扣（LeetCode）
69 #著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

    java

     1 class Solution {
 2     public int[] maxNumber(int[] nums1, int[] nums2, int k) {
 3         int m = nums1.length, n = nums2.length;
 4         int[] maxSubsequence = new int[k];
 5         int start = Math.max(0, k - n), end = Math.min(k, m);
 6         for (int i = start; i <= end; i++) {
 7             int[] subsequence1 = maxSubsequence(nums1, i);
 8             int[] subsequence2 = maxSubsequence(nums2, k - i);
 9             int[] curMaxSubsequence = merge(subsequence1, subsequence2);
10             if (compare(curMaxSubsequence, 0, maxSubsequence, 0) > 0) {
11                 System.arraycopy(curMaxSubsequence, 0, maxSubsequence, 0, k);
12             }
13         }
14         return maxSubsequence;
15     }
16 
17     public int[] maxSubsequence(int[] nums, int k) {
18         int length = nums.length;
19         int[] stack = new int[k];
20         int top = -1;
21         int remain = length - k;
22         for (int i = 0; i < length; i++) {
23             int num = nums[i];
24             while (top >= 0 && stack[top] < num && remain > 0) {
25                 top--;
26                 remain--;
27             }
28             if (top < k - 1) {
29                 stack[++top] = num;
30             } else {
31                 remain--;
32             }
33         }
34         return stack;
35     }
36 
37     public int[] merge(int[] subsequence1, int[] subsequence2) {
38         int x = subsequence1.length, y = subsequence2.length;
39         if (x == 0) {
40             return subsequence2;
41         }
42         if (y == 0) {
43             return subsequence1;
44         }
45         int mergeLength = x + y;
46         int[] merged = new int[mergeLength];
47         int index1 = 0, index2 = 0;
48         for (int i = 0; i < mergeLength; i++) {
49             if (compare(subsequence1, index1, subsequence2, index2) > 0) {
50                 merged[i] = subsequence1[index1++];
51             } else {
52                 merged[i] = subsequence2[index2++];
53             }
54         }
55         return merged;
56     }
57 
58     public int compare(int[] subsequence1, int index1, int[] subsequence2, int index2) {
59         int x = subsequence1.length, y = subsequence2.length;
60         while (index1 < x && index2 < y) {
61             int difference = subsequence1[index1] - subsequence2[index2];
62             if (difference != 0) {
63                 return difference;
64             }
65             index1++;
66             index2++;
67         }
68         return (x - index1) - (y - index2);
69     }
70 }
71 
72 
73 //作者：LeetCode-Solution
74 //链接：https://leetcode-cn.com/problems/create-maximum-number/solution/pin-jie-zui-da-shu-by-leetcode-solution/
75 //来源：力扣（LeetCode）
76 //著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

    思路差距

     目前我的水平处在被各路大佬的花活蒙蔽了双眼但自己玩不出来的尴尬境地，还是再多积累积累，巩固一下基础吧

    使用算法解决某个问题的时候，应该试着分解问题（但或许某些时候整体看待问题解决起来会比较巧妙，算了不管了，玄学吧）

    技术差距

     修改代码的时候出现了三个严重的技术问题，我分别针对测试用例进行讲解：

    1、list复制的问题，用result = stack是不对的，这样两者其实是引用同一组数据的关系，应该是result = stack[:]或者result = list(stack)

    注复制字符串的话只能是a = "".join(b)，a =

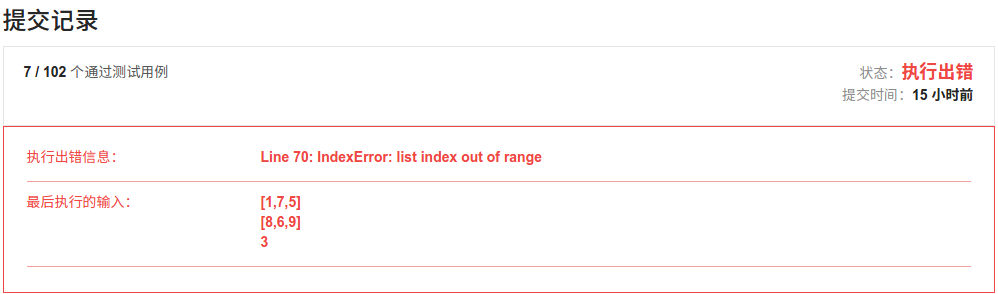
     2、实现单调栈时出栈的条件没有考虑全面，如果剩余的数字数量不再满足要求时，不能再继续出栈，应该立刻压栈保留长度。

     

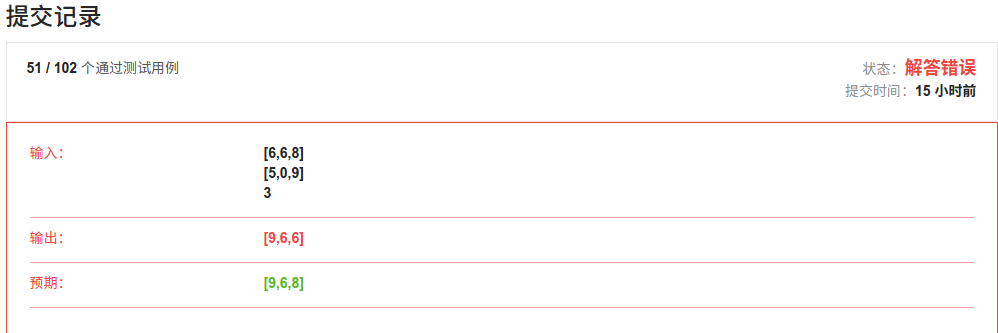
     3、遇到两个相同的数字的时候，判定条件欠考虑，需要接着判定相同数字后面几位的大小，还要考虑如果后面为空的情况。

     
  • 相关阅读:
    Jmeter 将正则表达式提取的参数传给全局（跨线程组使用变量）
    pod的状态分析
    前端 -- html介绍和head标签
    Python ----- 线程和进程
    网络编程 ------ 基础
    面向对象相关操作
    面向对象 --- 进阶篇
    python --- 面向对象
    python的模块和包的详细说明
    常用模块------时间模块 , random模块 ,os模块 , sys模块
  • 原文地址：https://www.cnblogs.com/monkiki/p/14078335.html
Copyright © 2011-2022 走看看