leetcode常规算法题复盘（第十三期）——最大矩形&柱状图中最大的矩形

题目原文

85. 最大矩形

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：

输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：6
解释：最大矩形如上图所示。

示例 2：

输入：matrix = []
输出：0

示例 3：

输入：matrix = [["0"]]
输出：0

示例 4：

输入：matrix = [["1"]]
输出：1

示例 5：

输入：matrix = [["0","0"]]
输出：0

提示：

• rows == matrix.length
• cols == matrix[0].length
• 0 <= row, cols <= 200
• matrix[i][j] 为 '0' 或 '1'

84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

 

图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

尝试解答

 最大矩形

思路沿用官方题解中的逐行确定外加单调栈，另外使用单调栈的过程中增设了”哨兵“简化代码：

class Solution {
    public int maximalRectangle(char[][] matrix) {
        if(matrix.length==0){
            return 0;
        }
        //先根据每行
        int row=matrix.length;
        int col=matrix[0].length;
        int res=0;
        int maxS=0;
        for (int i=0;i<row;i++){
            //i就是行标了
            int[] height = new int[col];
            for(int j=0;j<col;j++){
                //j就是列标
                for(int k=i;k>=0;k--){
                    if (matrix[k][j]=='1'){
                        height[j]++;
                    }
                    else{
//                        System.out.print(height[j]);
                        break;
                    }
                }
                //拿到了每列的高度值
            }
            Deque<Integer> stack = new ArrayDeque<>();
            int[] new_height = new int[col+2];
            for(int j=1;j<col+1;j++){
                new_height[j] = height[j-1];
            }
            new_height[col+1]=0;
            for(int j=0;j<new_height.length;j++){
                while(!stack.isEmpty() && new_height[j]<new_height[stack.peek()]){
                    int cur = stack.pop();
                    int l = stack.peek();
                    int r = j;
                    res = Math.max(res, (r - l - 1) * new_height[cur]);
                }
                
                stack.push(j);
            }
            res = Math.max(res,maxS);
        }
        return res;
    }
}

柱状图中最大的矩形

代码如下：

import java.util.ArrayDeque;
import java.util.Deque;

public class Solution {

    public int largestRectangleArea(int[] heights) {
        int len = heights.length;
        if (len == 0) {
            return 0;
        }

        if (len == 1) {
            return heights[0];
        }

        int res = 0;

        int[] newHeights = new int[len + 2];
        newHeights[0] = 0;
        System.arraycopy(heights, 0, newHeights, 1, len);
        newHeights[len + 1] = 0;
        len += 2;
        heights = newHeights;

        Deque<Integer> stack = new ArrayDeque<>(len);
        // 先放入哨兵，在循环里就不用做非空判断
        stack.addLast(0);
        
        for (int i = 1; i < len; i++) {
            while (heights[i] < heights[stack.peekLast()]) {
                int curHeight = heights[stack.pollLast()];
                int curWidth = i - stack.peekLast() - 1;
                res = Math.max(res, curHeight * curWidth);
            }
            stack.addLast(i);
        }
        return res;
    }

    public static void main(String[] args) {
        // int[] heights = {2, 1, 5, 6, 2, 3};
        int[] heights = {1, 1};
        Solution solution = new Solution();
        int res = solution.largestRectangleArea(heights);
        System.out.println(res);
    }
}

标准题解

最大矩形 

官方题解给了两种思路，其中思路一就是暴力解法，枚举所有可能的左上角与右下角，很明显这不是出题人想要看到的解法，不可能通过所有的测试用例，这里就不放方法一的源码了，直接看方法二——逐行确定最大面积的源码：

class Solution {
    public int maximalRectangle(char[][] matrix) {
        int m = matrix.length;
        if (m == 0) {
            return 0;
        }
        int n = matrix[0].length;
        int[][] left = new int[m][n];

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == '1') {
                    left[i][j] = (j == 0 ? 0 : left[i][j - 1]) + 1;
                }
            }
        }

        int ret = 0;
        for (int j = 0; j < n; j++) { // 对于每一列，使用基于柱状图的方法
            int[] up = new int[m];
            int[] down = new int[m];

            Deque<Integer> stack = new LinkedList<Integer>();
            for (int i = 0; i < m; i++) {
                while (!stack.isEmpty() && left[stack.peek()][j] >= left[i][j]) {
                    stack.pop();
                }
                up[i] = stack.isEmpty() ? -1 : stack.peek();
                stack.push(i);
            }
            stack.clear();
            for (int i = m - 1; i >= 0; i--) {
                while (!stack.isEmpty() && left[stack.peek()][j] >= left[i][j]) {
                    stack.pop();
                }
                down[i] = stack.isEmpty() ? m : stack.peek();
                stack.push(i);
            }

            for (int i = 0; i < m; i++) {
                int height = down[i] - up[i] - 1;
                int area = height * left[i][j];
                ret = Math.max(ret, area);
            }
        }
        return ret;
    }
}

//作者：LeetCode-Solution
//链接：https://leetcode-cn.com/problems/maximal-rectangle/solution/zui-da-ju-xing-by-leetcode-solution-bjlu/
//来源：力扣（LeetCode）
//著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

这道题要解决的子问题与《柱状图中的最大矩形》完全一样，即确定每一行上面所产生的最大矩形，具体思路可以看下面的柱状图中最大的矩形的单调栈题解。再次类比发现与之前的《接雨水》有异曲同工之处！https://www.cnblogs.com/monkiki/p/13893873.html

柱状图中最大的矩形

 方法一：对每一个矩形向左向右寻找边界，确定最大面积。代码如下：

暴力解法
这道问题的暴力解法比「接雨水」那道题要其实好想得多：可以枚举以每个柱形为高度的最大矩形的面积。

具体来说就是：依次遍历柱形的高度，对于每一个高度分别向两边扩散，求出以当前高度为矩形的最大宽度多少。

为此，我们需要：

左边看一下，看最多能向左延伸多长，找到大于等于当前柱形高度的最左边元素的下标；

右边看一下，看最多能向右延伸多长；找到大于等于当前柱形高度的最右边元素的下标。

对于每一个位置，我们都这样操作，得到一个矩形面积，求出它们的最大值。

参考代码 :

public class Solution {

    public int largestRectangleArea(int[] heights) {
        int len = heights.length;
        // 特判
        if (len == 0) {
            return 0;
        }

        int res = 0;
        for (int i = 0; i < len; i++) {

            // 找左边最后 1 个大于等于 heights[i] 的下标
            int left = i;
            int curHeight = heights[i];
            while (left > 0 && heights[left - 1] >= curHeight) {
                left--;
            }

            // 找右边最后 1 个大于等于 heights[i] 的索引
            int right = i;
            while (right < len - 1 && heights[right + 1] >= curHeight) {
                right++;
            }

            int width = right - left + 1;
            res = Math.max(res, width * curHeight);
        }
        return res;
    }
}

//作者：liweiwei1419
//链接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/bao-li-jie-fa-zhan-by-liweiwei1419/
//来源：力扣（LeetCode）
//著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

复杂度分析：

时间复杂度：O(N^2)O(N^2)，这里 NN 是输入数组的长度。

空间复杂度：O(1)O(1)。

看到时间复杂度为 O(N^2)O(N^2) 和空间复杂度为 O(1)O(1) 的组合，那么我们是不是可以一次遍历，不需要中心扩散就能够计算出每一个高度所对应的那个最大面积矩形的面积呢？

其实很容易想到的优化的思路就是「以空间换时间」。我们需要在遍历的过程中记录一些信息。

作者：liweiwei1419
链接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/bao-li-jie-fa-zhan-by-liweiwei1419/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

方法二：以空间换时间，用到的数据结构是栈
说明：下面文字有点长，大家可以直接收看 官方题解。

要搞清楚这个过程，请大家一定要在纸上画图，搞清楚一些细节，这样在编码的时候就不容易出错了。

记录什么信息呢？记录高度是不是可以呢？其实是不够的，因为计算矩形还需要计算宽度，很容易知道宽度是由下标确定的，记录了下标其实对应的高度就可以直接从输入数组中得出，因此，应该记录的是下标。

我们就拿示例的数组 [2, 1, 5, 6, 2, 3] 为例：

1、一开始看到的柱形高度为 2 ，这个时候以这个 2 为高度的最大面积的矩形还不能确定，我们需要继续向右遍历，如下图。

 

2、然后看到到高度为 1 的柱形，这个时候以这个柱形为高度的矩形的最大面积还是不知道的。但是它之前的以 2 为高度的最大面积的矩形是可以确定的，这是因为这个 1 比 2 小 ，因为这个 1 卡在了这里 2 不能再向右边扩展了，如下图。

 

我们计算一下以 2 为高度的最大矩形的面积是 2。其实这个时候，求解这个问题的思路其实已经慢慢打开了。如果已经确定了一个柱形的高度，我们可以无视它，将它以虚框表示，如下图。

 

3、遍历到高度为 5 的柱形，同样的以当前看到柱形为高度的矩形的最大面积也是不知道的，因为我们还要看右边高度的情况。那么它的左右有没有可以确定的柱形呢？没有，这是因为 5 比 1 大，我们看后面马上就出现了 6，不管是 1 这个柱形还是 5 这个柱形，都还可以向右边扩展；

 

4、接下来，遍历到高度为 6 的柱形，同样的，以柱形 1、5、6 为高度的最大矩形面积还是不能确定下来；

 

5、再接下来，遍历到高度为 2 的柱形。

 

发现了一件很神奇的事情，高度为 6 的柱形对应的最大矩形的面积的宽度可以确定下来，它就是夹在高度为 5 的柱形和高度为 2 的柱形之间的距离，它的高度是 6，宽度是 1。

 

将可以确定的柱形设置为虚线。

 

接下来柱形 5 对应的最大面积的矩形的宽度也可以确定下来，它是夹在高度为 1 和高度为 2 的两个柱形之间的距离；

 

确定好以后，我们将它标成虚线。

 

我们发现了，只要是遇到了当前柱形的高度比它上一个柱形的高度严格小的时候，一定可以确定它之前的某些柱形的最大宽度，并且确定的柱形宽度的顺序是从右边向左边。
这个现象告诉我们，在遍历的时候需要记录的信息就是遍历到的柱形的下标，它一左一右的两个柱形的下标的差就是这个面积最大的矩形对应的最大宽度。

这个时候，还需要考虑的一个细节是，在确定一个柱形的面积的时候，除了右边要比当前严格小，其实还蕴含了一个条件，那就是左边也要比当前高度严格小。

那如果是左边的高度和自己相等怎么办呢？我们想一想，我们之前是只要比当前严格小，我们才可以确定一些柱形的最大宽度。只要是大于或者等于之前看到的那一个柱形的高度的时候，我们其实都不能确定。

因此我们确定当前柱形对应的宽度的左边界的时候，往回头看的时候，一定要找到第一个严格小于我们要确定的那个柱形的高度的下标。这个时候 中间那些相等的柱形其实就可以当做不存在一样。因为它对应的最大矩形和它对应的最大矩形其实是一样的。

说到这里，其实我们的思路已经慢慢清晰了。

我们在遍历的时候，需要记录的是下标，如果当前的高度比它之前的高度严格小于的时候，就可以直接确定之前的那个高的柱形的最大矩形的面积，为了确定这个最大矩形的左边界，我们还要找到第一个严格小于它的高度的矩形，向左回退的时候，其实就可以当中间这些柱形不存在一样。

这是因为我们就是想确定 6 的宽度，6 的宽度确定完了，其实我们就不需要它了，这个 5 的高度和这个 5 的高度确定完了，我们也不需要它了。

我们在缓存数据的时候，是从左向右缓存的，我们计算出一个结果的顺序是从右向左的，并且计算完成以后我们就不再需要了，符合后进先出的特点。因此，我们需要的这个作为缓存的数据结构就是栈。

当确定了一个柱形的高度的时候，我们就将它从栈顶移出，所有的柱形在栈中进栈一次，出栈一次，一开始栈为空，最后也一定要让栈为空，表示这个高度数组里所有的元素都考虑完了。

6、最后遍历到最后一个柱形，即高度为 3 的柱形。

 

（一次遍历完成以后。接下来考虑栈里的元素全部出栈。）

接下来我们就要依次考虑还在栈里的柱形的高度。和刚才的方法一样，只不过这个时候右边没有比它高度还小的柱形了，这个时候计算宽度应该假设最右边还有一个下标为 len （这里等于 6） 的高度为 0 （或者 0.5，只要比 1 小）的柱形。

 

7、下标为 5 ，即高度为 3 的柱形，左边的下标是 4 ，右边的下标是 6 ，因此宽度是 6 - 4 - 1 = 1（两边都不算，只算中间的距离，所以减 1）；算完以后，将它标为虚线。

 

8、下标为 4 ，高度为 2 的柱形，左边的下标是 1 ，右边的下标是 6 ，因此宽度是 6 - 1 - 1 = 4；算完以后，将它标为虚线。

 

9、最后看下标为 1，高度为 1 的矩形，它的左边和右边其实都没有元素了，它就是整个柱形数组里高度最低的柱形，计算它的宽度，就是整个柱形数组的长度。

 

到此为止，所有的柱形高度对应的最大矩形的面积就都计算出来了。

 

这个算法经过一次遍历，在每一次计算最大宽度的时候，没有去遍历，而是使用了栈里存放的下标信息，以 O(1)O(1) 的时间复杂度计算最大宽度。

参考代码(增加哨兵)：

import java.util.ArrayDeque;
import java.util.Deque;

public class Solution {

    public int largestRectangleArea(int[] heights) {
        int len = heights.length;
        if (len == 0) {
            return 0;
        }

        if (len == 1) {
            return heights[0];
        }

        int res = 0;

        int[] newHeights = new int[len + 2];
        newHeights[0] = 0;
        System.arraycopy(heights, 0, newHeights, 1, len);
        newHeights[len + 1] = 0;
        len += 2;
        heights = newHeights;

        Deque<Integer> stack = new ArrayDeque<>(len);
        // 先放入哨兵，在循环里就不用做非空判断
        stack.addLast(0);
        
        for (int i = 1; i < len; i++) {
            while (heights[i] < heights[stack.peekLast()]) {
                int curHeight = heights[stack.pollLast()];
                int curWidth = i - stack.peekLast() - 1;
                res = Math.max(res, curHeight * curWidth);
            }
            stack.addLast(i);
        }
        return res;
    }

    public static void main(String[] args) {
        // int[] heights = {2, 1, 5, 6, 2, 3};
        int[] heights = {1, 1};
        Solution solution = new Solution();
        int res = solution.largestRectangleArea(heights);
        System.out.println(res);
    }
}

//作者：liweiwei1419
//链接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/bao-li-jie-fa-zhan-by-liweiwei1419/
//来源：力扣（LeetCode）
//著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

思路差距

 因为分析问题的能力还是有些欠缺，目前的状态是：拿到题目后，大概能想到几种解决方法，但是对每种方法的代价、实现难度缺乏一个准确的认识，导致最终确定不了解题方法，无法快速写出代码完成题目（跟力扣大佬的差距实在是大的要命）。我认为产生这种现象的原因有这几点：

1、积累的解题思路仍然太少，对已经接触过的思路仍不能熟练运用；

2、没有静下心来细致完整的分析题目，真正完整的解题过程需要先按照题意将过程完整分析一遍，这其中先不要套用任何技巧，因为这样很可能会让你漏掉一些细节，分析完后再考虑计算简化，应该遵循的分析过程是：理解题意，先”暴力“走通一遍，最后寻找简化方法。

3、技术力欠缺，对语言不够熟悉。

对于1、2点举个例子：拿到《最大矩形》的题目后，首先要做的就是拆解这个问题，将问题拆解为：对每一行柱形图的最大矩形，之后我们应该先”暴力”走通一遍，因为我们现在还并不清楚具体套用什么思路，即使这样的暴力解法最后肯定会超出时间限制，之后，我们分析这个暴力解法，看看有那些地方被重复计算了，开始抠细节，通过确定单调栈的方法将每次必须计算左右边界的过程巧妙地规避掉（因为在暴力解法中，对每一个柱形都要找到离它最近的小于它的柱形，左边右边都要各求一次，这时就有灵感了，“离他最近的小于他的”！我们用栈来记录之前遇到的最近的小于此数的下标不就好了吗，于是使用单调栈，为了让单调栈更容易实现，我们在数组两头各安插一个数值为0的“哨兵”，这才使用哨兵，这个顺序不能混乱，否则题目很难解出来。），这才是解答一道复杂题的正确方式，并不是读到题目后觉得与之前哪道题眼熟就强行去套之前那道题的思路，这样多半不会成功。

对stack（栈）与queue（队列）的一点认识

非常神奇的两种数据结构，栈总是在操作最顶端的那个数据，这其中涉及到了“比较”、“进栈”、“出栈”，需要强调的是，不管前面经历了什么，栈操作的永远是最顶端的那【一个】数据，因此涉及到栈的问题往往带有“最近的xxxx”、“最先xxxx”以及等字眼；而队列就给人一种“众生平等”的感觉，先进先出，后进后出，进入队列有一套标准，弹出队列也有一套保准。

技术差距

 1、“哨兵”技巧，设置哨兵是为了减少比较次数，省去对下标越界的判断。这里转载一位CSDN大佬的博客内容

https://blog.csdn.net/Lison_Zhu/article/details/77500811?utm_medium=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.control&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.control

 

 

 

 

 

 2、System.arraycopy

 

3、java双向队列Deque栈与队列

此处转载CSDN大佬@森林屿麓的博客https://blog.csdn.net/u013967628/article/details/85210036

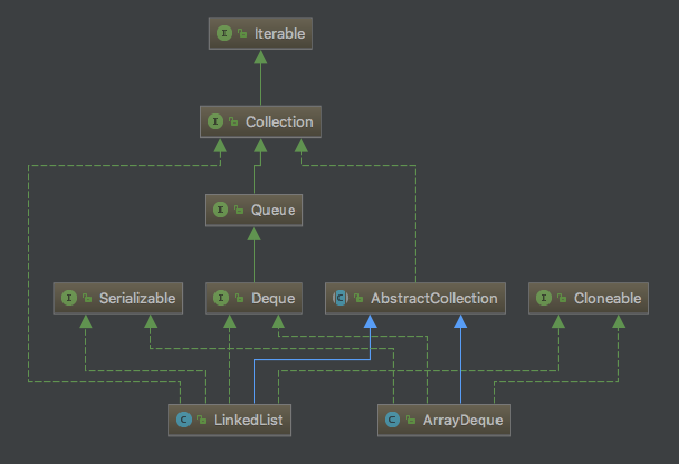
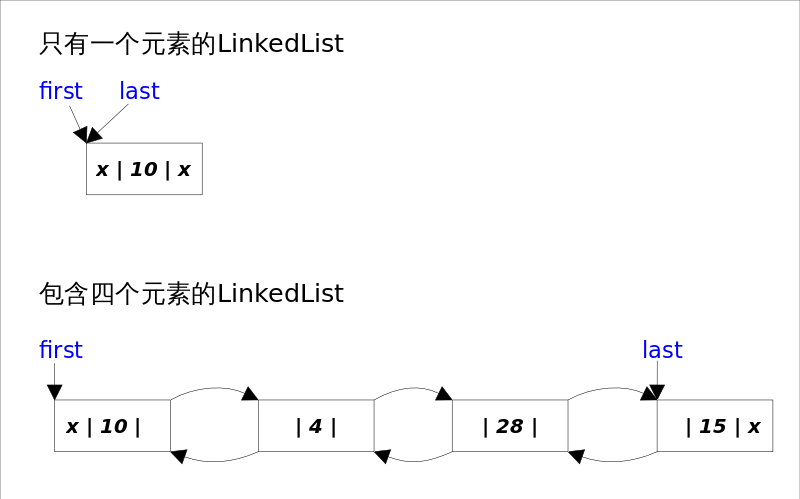
Java中实际上提供了java.util.Stack来实现栈结构,但官方目前已不推荐使用,而是使用java.util.Deque双端队列来实现队列与栈的各种需求.如下图所示java.util.Deque的实现子类有java.util.LinkedList和java.util.ArrayDeque.顾名思义前者是基于链表,后者基于数据实现的双端队列.

总体介绍

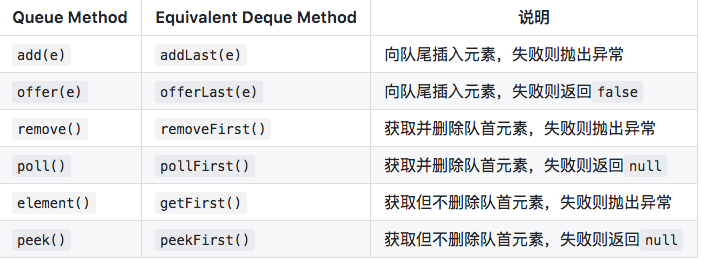
要讲栈和队列，首先要讲Deque接口。Deque的含义是“double ended queue”，即双端队列，它既可以当作栈使用，也可以当作队列使用。下表列出了Deque与Queue相对应的接口：

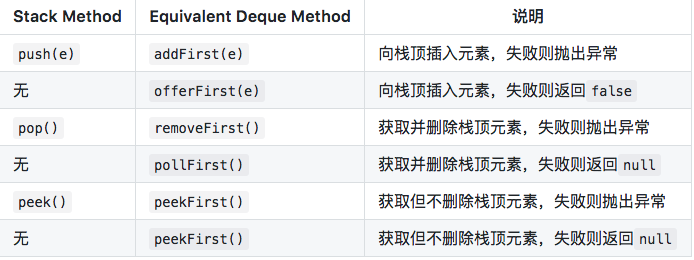
下表列出了Deque与Stack对应的接口：

上面两个表共定义了Deque的12个接口。添加，删除，取值都有两套接口，它们功能相同，区别是对失败情况的处理不同。一套接口遇到失败就会抛出异常，另一套遇到失败会返回特殊值（false或null）。除非某种实现对容量有限制，大多数情况下，添加操作是不会失败的。虽然Deque的接口有12个之多，但无非就是对容器的两端进行操作，或添加，或删除，或查看。明白了这一点讲解起来就会非常简单。

ArrayDeque

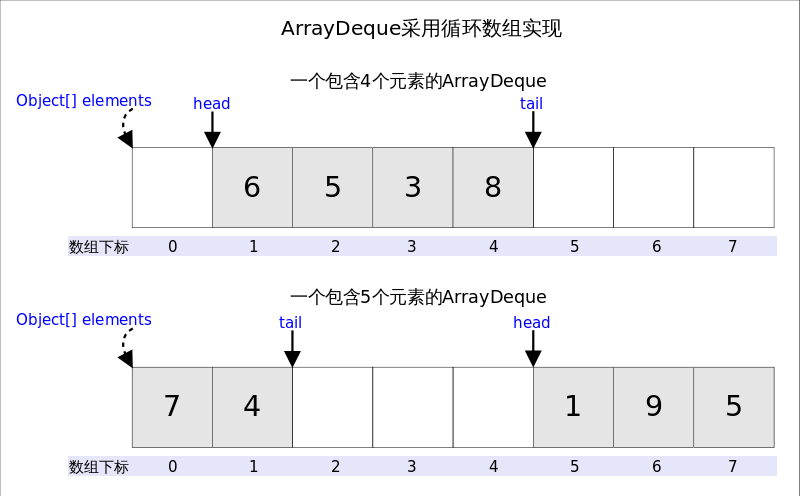
从名字可以看出ArrayDeque底层通过数组实现，为了满足可以同时在数组两端插入或删除元素的需求，该数组还必须是循环的，即循环数组（circular array），也就是说数组的任何一点都可能被看作起点或者终点。ArrayDeque是非线程安全的（not thread-safe），当多个线程同时使用的时候，需要程序员手动同步；另外，该容器不允许放入null元素。

上图中我们看到，head指向首端第一个有效元素，tail指向尾端第一个可以插入元素的空位。因为是循环数组，所以head不一定总等于0，tail也不一定总是比head大。

addFirst()

针对首端插入实际需要考虑：1.空间是否够用，以及2.下标是否越界的问题。上图中，如果head为0之后接着调用addFirst()，虽然空余空间还够用，但head为-1，下标越界了。下列代码很好的解决了这两个问题。

1.  
   public void addFirst(E e) {
2.  
   if (e == null)
3.  
   throw new NullPointerException();
4.  
   //下标越界问题解决方案
5.  
   elements[head = (head - 1) & (elements.length - 1)] = e;
6.  
   //容量问题解决方案
7.  
   if (head == tail)
8.  
   doubleCapacity();
9.  
   }

上述代码我们看到，空间问题是在插入之后解决的，因为tail总是指向下一个可插入的空位，也就意味着elements数组至少有一个空位，所以插入元素的时候不用考虑空间问题。

下标越界的处理解决起来非常简单，head = (head - 1) & (elements.length - 1)就可以了，这段代码相当于取余，同时解决了head为负值的情况。因为elements.length必需是2的指数倍(构造函数初始化逻辑保证)，elements - 1就是二进制低位全1，跟head - 1相与之后就起到了取模的作用，如果head - 1为负数（其实只可能是-1），则相当于对其取相对于elements.length的补码。

下面再说说扩容函数doubleCapacity()，其逻辑是申请一个更大的数组（原数组的两倍），然后将原数组复制过去。过程如下图所示：

 

图中我们看到，复制分两次进行，第一次复制head右边的元素，第二次复制head左边的元素。

1.  
   private void doubleCapacity() {
2.  
   assert head == tail;
3.  
   int p = head;
4.  
   int n = elements.length;
5.  
   int r = n - p; // number of elements to the right of p
6.  
   int newCapacity = n << 1;
7.  
   if (newCapacity < 0)
8.  
   throw new IllegalStateException("Sorry, deque too big");
9.  
   Object[] a = new Object[newCapacity];
10.  
    System.arraycopy(elements, p, a, 0, r);
11.  
    System.arraycopy(elements, 0, a, r, p);
12.  
    elements = a;
13.  
    head = 0;
14.  
    tail = n;
15.  
    }

addLast()

addLast(E e)的作用是在Deque的尾端插入元素，也就是在tail的位置插入元素，由于tail总是指向下一个可以插入的空位，因此只需要elements[tail] = e;即可。插入完成后再检查空间，如果空间已经用光，则调用doubleCapacity()进行扩容。与first比较类似就不多分析了.

其他操作也是差不多的方式,唯一麻烦的head与tail位置转换也用取余巧妙的化解了.

LinkedList

LinkedList实现了Deque接口,因此其具备双端队列的特性,由于其是链表结构,因此不像ArrayDeque要考虑越界问题,容量问题,那么对应操作就很简单了,另外当需要使用栈和队列是官方推荐的是ArrayDeque,因此这里不做多的分析.