【Java源码】树-概述

树的基本术语

• 结点（node）由数据元素以及指向子树的地址构成。
• 若 X 结点有子树，则子树的根结点称为 X 的孩子（child）结点，相应地，
  X 称为其孩子的双亲（parents）结点，又称父母结点。
• 同一双亲的孩子结点之间互称兄弟（sibling）结点。
• 叶子（leaf）结点是指度为 0 的结点，又称为终端结点。其他的叫分支结点

二叉树的定义

二叉树由一个根结点或两棵互不相交的、分别称为左子树和右子树的子二叉树构成。

二叉树的性质

• 二叉树的结点最多只有两棵子树

• 若根结点的层次为 1，则二叉树第 i 层的结点数目最多为 2^i-1（i≥1）个。

• 在深度为 k 的二叉树中，至多有 2^k -1 个结点（k≥0）。

• 二叉树中，若叶子结点数为 n0，度为 2 的结点数为 n2，则有 n0=n2+1。

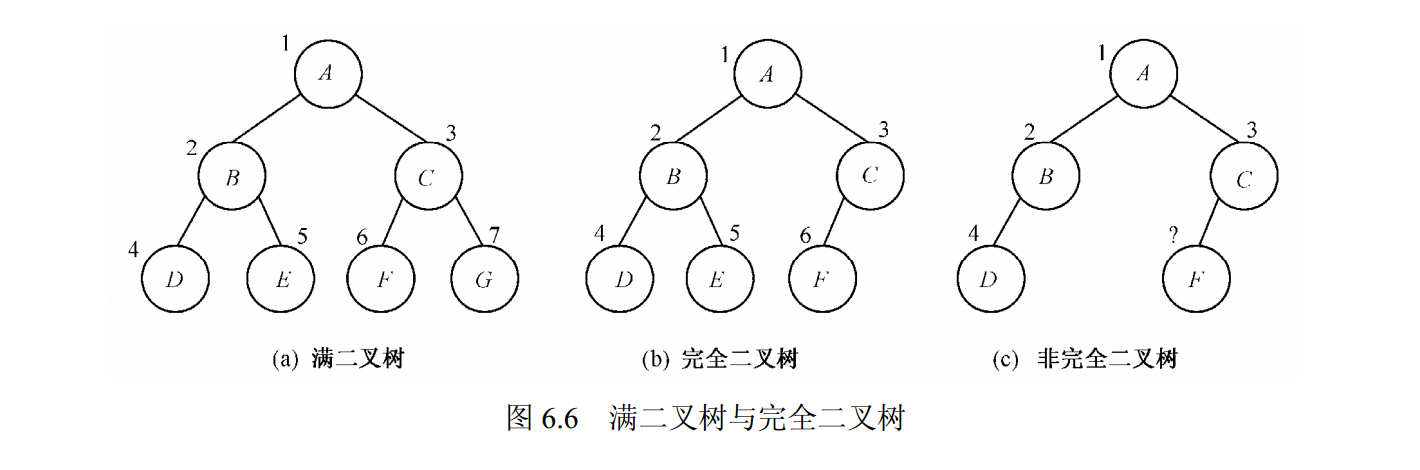
• 满二叉树:一棵深度为 k 的满二叉树（full binary tree）是具有 2^k -1 （k≥0）个结点的二叉树。满二叉树每一层的结点数目都达到最大值.

• 完全二叉树:一棵具有 n 个结点深度为 k 的二叉树，如果它的每一个结点都与深度为 k 的满二叉树中编
  号为 1～n 的结点一一对应，则称这棵二叉树为完全二叉树（complete binary tree）

二叉树的存储结构

二叉树的存储结构有两种：顺序存储结构和链式存储结构。

顺序存储

二叉树的顺序存储结构适用于完全二叉树，对完全二叉树进行顺序编号，将编号为 i 的结
点存放在数组下标为 i-1 的位置上.

链式存储

一般情况下，采用链式存储结构来存储二叉树。每个结点有 3 个域：

• data 表示结点的数据元素。
• left 指向该结点的左孩子结点，即左子树的根结点。
• right 指向该结点的右孩子结点，即右子树的根结点。

二叉树的遍历

先根序遍历(DLR)

访问根结点，遍历左子树，遍历右子树。表达式的前缀表示（波兰式）

中根序遍历(LDR)

遍历左子树，访问根结点，遍历右子树。表达式的中缀表示

后根序遍历(LRD)

遍历左子树，遍历右子树，访问根结点。表达式的后缀表示（逆波兰式）

参考图书： 《算法与数据结构》