论文题目: AdderNet:Do We Really Need Multiplications in Deep Learning?
文献地址:https://arxiv.org/pdf/1912.13200v3.pdf
源码地址:https://github.com/huawei-noah/AdderNet(Pytorch 版)
从论文题目中可以意会出这篇paper是要将CNN网络中乘积操作尽可能的全部替换为加法操作,也就是对CNN操作的改进,而不是提出某种网络结构。当然,改进的效果需要达到和CNN差不多的精度或者更好的精度。
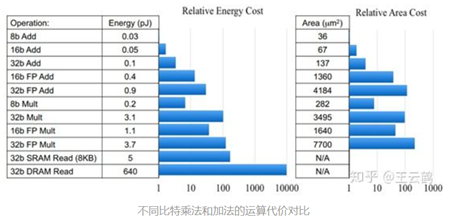
众所周知,在硬件平台中,加法操作相对于乘法操作都要更容易,更省时。在ARM中,进行一个乘法操作就会带来1μs的时间消耗。由于FPGA中运算的高速并发,才使得深度学习在硬件平台中移植成为了可能。虽然现在各种专用AI芯片、FPGA都对深度学习任务做了优化,算浮点乘法并不一定与加法消耗资源相差太大,但使用AdderNet可以减少芯片,板子的成本,同时可以应用于更轻巧的移动设备中。
AdderNet应用中的效果
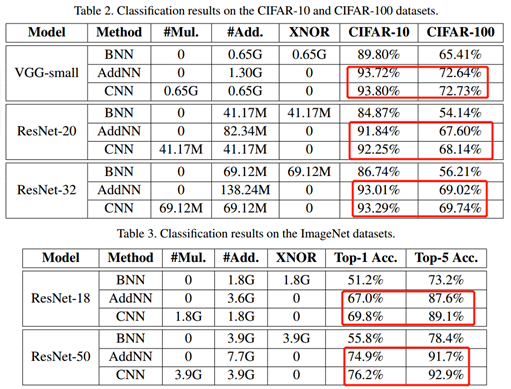
从CIFAR数据集和ImageNet数据集的实验结果可以看出,AdderNet减少了网络中的乘法操作的计算量,降低了计算能耗。但与CNN相比,虽然精度在数量级上差不多,但还是会存在少量的精度丢失。这其实在某一方面也对应了作者的题目,在深度学习中是否需要乘法?作者将这个问题抛出来,供专家、学者实践验证。
但值得注意的是, Doesn't AdderNet use multiplication at all? The answer is No.
卷积运算在深度学习中面临的问题
与廉价的加法运算相比,乘法运算具有更高的计算复杂度。深度神经网络广泛使用卷积操作,卷积操作中使用互相关来度量输入特征与卷积滤波器之间的相似性,包含大量的浮点运算。作者针对神经网络中大量的乘法的问题设计了修改思路,提出了AdderNets的卷积方式,使用加法运算降低运算成本。
将CNN卷积过程中的乘法操作换为加法操作,需要对模型训练的多种规则进行修改:
- 使用L1距离作为各层卷积核与输入特征相互作用的计算方式;
- 设计了改进的包含正则的梯度计算方式;
- 提出了一种针对各层学习率的自适应策略。
随着图形处理单元(GPU)的出现,具有数十亿个浮点数乘法的深度卷积神经网络(CNNs)可以加速并在各种计算机视觉任务中取得重要进展。例如:图像分类、目标检测、分割以及人脸验证。而这些高能耗的GPU设备难以部署到移动设备从而限制了先进的深度学习系统的应用(RTX 2080Ti, 250W +)。【现有的GPU不够轻巧,不能轻易的安装在移动设备上,虽然GPU本身是一张卡中很小的一部分,但是仍然需要许多其他的硬件来支撑它的使用,如存储芯片、能源器件等】。这也是为什么要研究更加高效的深度神经网络,从而使模型可以在负担的起的移动设备资源上运行。
简而言之,虽然GPU可以满足大量浮点数乘法的运算,但由于GPU不够轻巧,难以安装在更加轻巧的移动设备上,使应用场景有一定限制。
二值化的卷积核可以显著的减少计算消耗,但原来的识别精度将无法保持。此外,二值网络的训练过程不稳定。
实现思路
1. 卷积操作的替代品 -- L1距离
直观理解
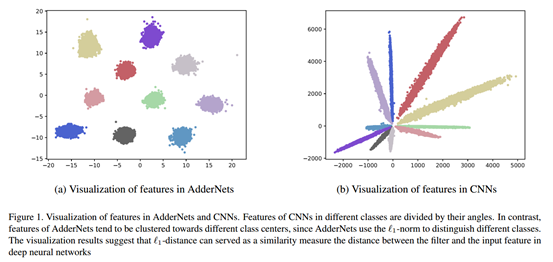
首先,作者对使用L1距离代替卷积操作的合理性进行了可视化的展示。如下图所示,左图是使用L1 距离的AdderNet, 右图为使用CNN卷积操作。不难看出,CNN中根据不同的类别特征的角度进行区分;AdderNets中是根据类的中心点,不同的类别聚成一簇。从特征的分布图可以直观的说明,L1距离能够作为一个合适的指标去量化特征值和输入之间的距离。
理论理解
对于卷积操作,假定F是卷积核,X为输入特征,Y为输出特征,那么卷积操作的计算可以定义为如下操作。直觉上,下式的形式与模板匹配很像,F相当于模板,整个过程相当于计算输入特征X与F的相似匹配程度。
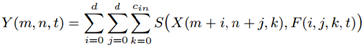
其中,S( · )为预定义的相似度量方式。如果S为乘法操作,上式就是卷积操作的方式,而乘法操作构成的上式正好是L2-范数的表达,也就是说CNN是L2-范数;如果d=1,就是全连接操作。
通过上式和之前的描述,作者的意图是寻找一个距离指标S,而这个S操作基本上不用或者少用乘法。
不难想象,可以尝试使用L1-范数来代替L2-范数。恰好,作者便是使用L1-范数距离作为预定义的相似度量方式S,如下式所示:
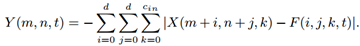
其中的减法在运算中可以用补码的方式转化为加法,这样就能够得到不包含乘法运算的相似性度量方法。
卷积核通过权重作用于特征值再加和的方式,其输出可能是正值也可能是负值。而adder核的输出总是负值。因此,作者使用BN操作,这样可以使adder操作规范化到一定的范围。这样,所有的激活函数便都可以作用于adderNets上(否则还要设计激活函数)。虽然BN操作中包含乘法运算,但是运算量相较于卷积中的运算可以忽略不计。
CNN和AdderNet的计算复杂度可以分别表示为:
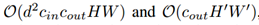
2. 优化方法
sgn(·) --》 full precision gradient(无sgn) --》 Hard-Tanh(full-precision gradient)
在CNN中,输出特征Y对卷积核F的偏导数如下式所示(乘法求偏导)。

在AdderNets中,偏导为:
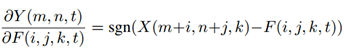
其中,sgn( · )为信号函数,使得梯度只有可能是±1和0。
然而,上述偏导只能通过signSGD进行更新,然而,signSGD不会沿着梯度最陡峭的方向下降,并且性能会随着维度的增大而下降。因此,作者认为signSGD不适合用于具有大量参数的神经网络。因此,作者又选取了一种替代方式 ---- full precision gradient。 从形式上看,即为去掉外层的sgn( · ):
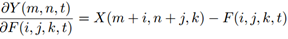
然而,采用full precision gradient的方式也会带来一个问题,full-precision gradient的值有可能比1大或者比-1小,这样的梯度在链式求导法则中极易造成梯度爆炸的现象。
由于链式求导法则,梯度不仅仅影响当前层卷积核Fi本身,还会影响之前的层。
因此, 还需要对梯度值进行约束,作者采用HardTanh粗暴的对梯度值进行截断,最终梯度的形式:
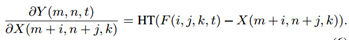
其中,HT( · )表示HardTanh函数,具体表达形式如下:
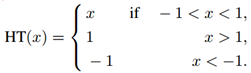
这里关于梯度的描述中,可以感觉到反向传播过程中,可以不严格按照求偏导的方式进行
3. 自适应学习率
首先,作者比较了CNNs和AdderNets输出的方差【训练发生的偏移-- BN来解决】:
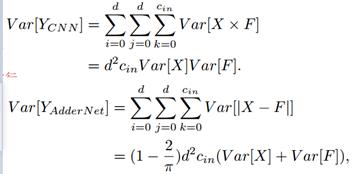
实际中,权重的方差Var[F]的值通常特别小,在CNN中大约是10^-3 或者 10^-4这样的数量级。这样,比较上述CNN和AdderNet的方差,CNN中Var[X]乘以Var[F]这样特别小的值,其方差的输出要比AdderNet中Var[X] + Var[F]这样特别小的值要小的多。也就是说,AdderNet输出的方差要比CNN的大得多【AdderNet输出具有大方差】。 --添加BN
为了促进激活函数的功能,在每一层后都添加BN操作:
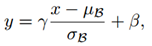
其中,γ和β是训练的超参数;μ和σ分别代表输入的均值和方差。
因此,梯度的公式可以计算为:
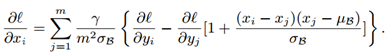
可以看出,AdderNet的梯度远小于CNN。作者在MNIST数据集中对比了AdderNet和CNN前三层的梯度,如下表所示。梯度值小会造成卷积核参数更新缓慢。

对于这样的问题,一个很直接的想法就是采用一个较大的学习率。然而从表1中可以看出,Adder Net中不同层之间的梯度相差较大,因此,难以使用统一的学习率。也就是说,需要针对各层设计自适应的学习率。每一层学习率更新的方式:
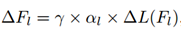
其中,γ是全局学习率;ΔL(Fl)是第l层的梯度;αl是l层的学习率。
αl的确定是通过卷积核中的参数量确定的:
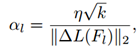
其中,k表示卷积核中的参数量;η表示是用于控制adder单元学习率的超参数。
前向和反向的计算过程如下所示:

对各卷积核进行可视化:

从卷积核的可是化来看,AdderNet的卷积核与CNNs一致,并不是二值化的网络。
权重分布可视化
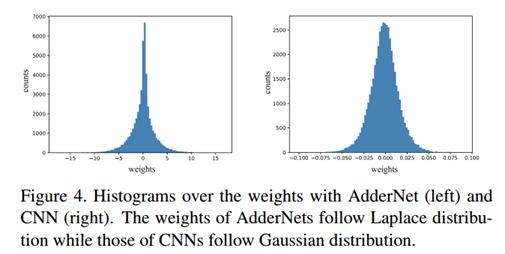
AdderNet服从拉普拉斯分布,CNN服从高斯分布。
总结
AdderNets与卷积神经网络(CNNs)非常相似,卷积神经网络通过卷积核从输入数据或者图像中提取特征。现在为了找出与CNN的不同之处,CNN相当于使用L2-范数,它要求浮点值之间进行大量的乘法运算,使得计算成本高。但是L2-范数不是确定两个向量距离的唯一方法。AdderNets中使用了另一种类型的范数:向量的L1-范数来找出输入特征和滤波器之间的区别,使用减法代替了卷积操作中的乘法。由于L1-范数在向量分量之间使用减法(加法的补码),所以AdderNet的计算成本相对于CNN而言是非常低的。而设计的特殊的反向传播方法全精度梯度和自适应学习率会使得AdderNet更加高效。
AdderNet中并没有完全不使用乘法操作,BN操作中包含乘法操作,只不过相对于CNNs中的乘法操作的数量来说,是可以忽略不计的。
只不过... 在AdderNet中关于梯度和自适应学习率的设计的改进,虽然有可圈可点之处,但处理方式上未免有些"拿来主义"的暴力解决。毕竟是实习生领衔打造,改进风格上让我想起了我读研时发的那篇SCI...