OSU!

题源

题面

 

---

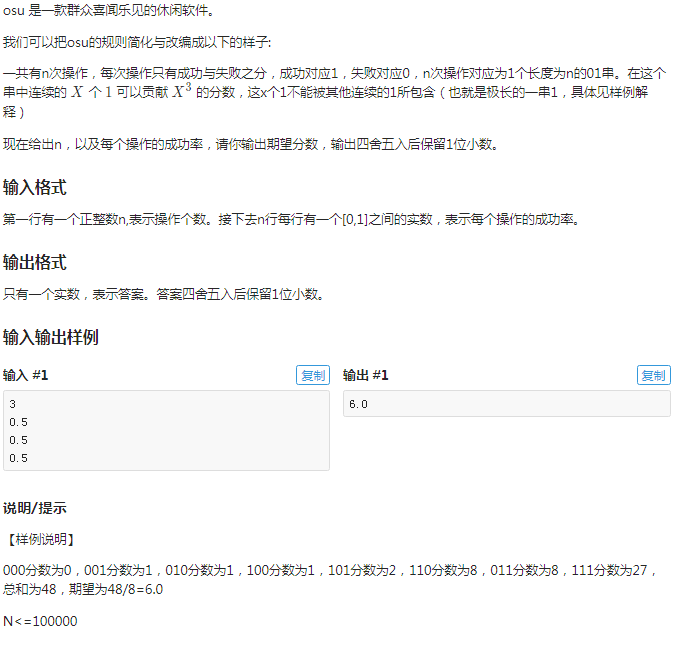
我们设  f [ i ] 为 E( len(i) ) ， ff [ i ] 为 E ( len( i ) ^2 )  ， fff [ i ] 为 E( len( i ) ^ 3 )

由于期望有可加性

所以 E ( i  ) = E ( i - 1 ) + E ( 1 ) 

f[i]=(f[i-1]+1)*p[i]

同理 E ( i ^ 2 ) = E ( (i-1)^2 + 2*( i-1 ) +1 ) = E( ( i -1 )^2 ) + 2*E ( i-1 ) +E ( 1 ) 

ff[i]=(ff[i-1]+2*f[i-1]+1)*p[i]

我们发现其实 E( i ^ k ) 就长得像 二项式展开 一样了

 

时间 O(n) ， 空间O( n ) 也可以滚成 O( 1 )

---

Code :    57ms / 3.60MB

#include<stdio.h>
#define ld double
#define For(i,a,b) for(register int i=(a);i<=(b);i++)
using namespace std;
const int maxn=1e5+10;
int n;
ld p[maxn],f[maxn],ff[maxn],fff[maxn];
signed main(){
    scanf("%d",&n);
    For(i,1,n){
        scanf("%lf",&p[i]);
    }
    For(i,1,n){
        f[i]=(f[i-1]+1)*p[i],
        ff[i]=(ff[i-1]+2*f[i-1]+1)*p[i],
        fff[i]=fff[i-1]+(3*ff[i-1]+3*f[i-1]+1)*p[i];
    }
    printf("%.1lf",fff[n]);
}