zoukankan html css js c++ java

kuangbin基础数论专题题解

--老年菜鸡的基础数论之旅

A - Bi-shoe and Phi-shoe

Description

给定一个序列，序列每个值x有一个花费，x的花费为一个欧拉函数值大于等于x的数y，求最小花费

Solution

首先我们要使求得花费最小，那就找一个刚好满足欧拉函数值大于等于x的数嘛，然后我们知道素数p的欧拉函数值为p-1，所以我们可以从x+1开始找，就减少了查找区间，降低了复杂度

 1 #include <bits/stdc++.h>
 2 #define lson rt << 1, l, mid
 3 #define rson rt << 1 | 1, mid + 1, r
 4 using namespace std;
 5 using ll = long long;
 6 using ull = unsigned long long;
 7 using pa = pair<int, int>;
 8 using ld = long double;
 9 const int maxn = 1e6 + 1e5;
10 int n, m, k;
11 int p[maxn], e[maxn];
12 void init()
13 {
14     for (int i = 2; i < maxn; i++)
15         e[i] = i;
16     for (int i = 2; i < maxn; ++i)
17     {
18         if (e[i] == i)
19         {
20             for (int j = i; j < maxn; j += i)
21                 e[j] = e[j] / i * (i - 1);
22         }
23     }
24 }
25 int main(int argc, char const *argv[])
26 {
27     ios::sync_with_stdio(false);
28     cin.tie(0);
29     cout.tie(0);
30     init();
31     int t;
32     cin >> t;
33     int c = 1;
34     while (t--)
35     {
36         ll ans = 0;
37         cin >> n;
38         for (int i = 0; i < n; i++)
39         {
40             int x;
41             cin >> x;
42             for (int j = x + 1; j < maxn; j++)
43                 if (e[j] >= x)
44                 {
45                     ans += j;
46                     break;
47                 }
48         }
49         cout << "Case " << c << ": " << ans << " Xukha
";
50         ++c;
51     }
52     return 0;
53 }

View Code

B - Prime Independence

Description

给定一个序列，要求求出序列中的最大分配集，一个分配集里的数不能出现两两相除商不是素数的情况

Solution

质因子分解建二分图，由于没有左右关系，我们可以建双向边，最后结果除以2就是原图最大匹配，然后跑最大匹配

最大独立集=|V|-最大匹配，所以最后答案最大独立集应该是|V|-maxMatch()/2

这题数据范围比较大，4e4的点集，用匈牙利会t，需要用HK算法跑最大匹配

还有一种是根据质因子的奇偶性来建边，这样建的图跑出来就没有重复的匹配，不过还没理解

看大佬博客是根据总的质因子数奇偶性建边，相同奇偶性的放一边（雾）

  1 #include <bits/stdc++.h>
  2 #define lson rt << 1, l, mid
  3 #define rson rt << 1 | 1, mid + 1, r
  4 using namespace std;
  5 using ll = long long;
  6 using ull = unsigned long long;
  7 using pa = pair<int, int>;
  8 using ld = long double;
  9 int n, m, k;
 10 const int maxE = 5e5 + 10;
 11 const int maxn = 4e4 + 10;
 12 const int INF = 0x3f3f3f3f;
 13 vector<int> G[maxn];
 14 int uN;
 15 int Mx[maxn], My[maxn];
 16 int dx[maxn], dy[maxn];
 17 int dis;
 18 bool used[maxn];
 19 bool SearchP()
 20 {
 21     queue<int> Q;
 22     dis = INF;
 23     memset(dx, -1, sizeof(dx));
 24     memset(dy, -1, sizeof(dy));
 25     for (int i = 1; i <= uN; i++)
 26         if (Mx[i] == -1)
 27         {
 28             Q.push(i);
 29             dx[i] = 0;
 30         }
 31     while (!Q.empty())
 32     {
 33         int u = Q.front();
 34         Q.pop();
 35         if (dx[u] > dis)
 36             break;
 37         int sz = G[u].size();
 38         for (int i = 0; i < sz; i++)
 39         {
 40             int v = G[u][i];
 41             if (dy[v] == -1)
 42             {
 43                 dy[v] = dx[u] + 1;
 44                 if (My[v] == -1)
 45                     dis = dy[v];
 46                 else
 47                 {
 48                     dx[My[v]] = dy[v] + 1;
 49                     Q.push(My[v]);
 50                 }
 51             }
 52         }
 53     }
 54     return dis != INF;
 55 }
 56 bool DFS(int u)
 57 {
 58     int sz = G[u].size();
 59     for (int i = 0; i < sz; i++)
 60     {
 61         int v = G[u][i];
 62         if (!used[v] && dy[v] == dx[u] + 1)
 63         {
 64             used[v] = true;
 65             if (My[v] != -1 && dy[v] == dis)
 66                 continue;
 67             if (My[v] == -1 || DFS(My[v]))
 68             {
 69                 My[v] = u;
 70                 Mx[u] = v;
 71                 return true;
 72             }
 73         }
 74     }
 75     return false;
 76 }
 77 int MaxMatch()
 78 {
 79     int res = 0;
 80     memset(Mx, -1, sizeof(Mx));
 81     memset(My, -1, sizeof(My));
 82     while (SearchP())
 83     {
 84         memset(used, false, sizeof(used));
 85         for (int i = 1; i <= uN; i++)
 86             if (Mx[i] == -1 && DFS(i))
 87                 res++;
 88     }
 89     return res;
 90 }
 91 
 92 template <class T>
 93 inline void read(T &ret)
 94 {
 95     int f = 1;
 96     ret = 0;
 97     char ch = getchar();
 98     while (!isdigit(ch))
 99     {
100         if (ch == '-')
101             f = -1;
102         ch = getchar();
103     }
104     while (isdigit(ch))
105     {
106         ret = (ret << 1) + (ret << 3) + ch - '0';
107         ch = getchar();
108     }
109     ret *= f;
110 }
111 template <class T>
112 inline void write(T n)
113 {
114     if (n < 0)
115     {
116         putchar('-');
117         n = -n;
118     }
119     if (n >= 10)
120     {
121         write(n / 10);
122     }
123     putchar(n % 10 + '0');
124 }
125 int a[maxn];
126 int xx, tot = 1;
127 unordered_map<int, int> pos;
128 int prime[maxE];
129 int notp[maxE];
130 int pcnt;
131 inline void init()
132 {
133     for (int i = 2; i < maxE; i++)
134     {
135         if (!notp[i])
136         {
137             prime[pcnt++] = i;
138             for (int j = 0; j < pcnt && i * prime[j] < maxE; j++)
139             {
140                 notp[i * prime[j]] = 1;
141                 if (i % prime[j] == 0)
142                     break;
143             }
144         }
145     }
146 }
147 inline void add(int x, int id)
148 {
149     int fac[maxn / 10];
150     int tot = 0;
151     for (int i = 0; prime[i] * prime[i] <= x; i++)
152     {
153         if (x % prime[i] == 0)
154         {
155             fac[tot++] = prime[i];
156             while (x % prime[i] == 0)
157                 x /= prime[i];
158         }
159     }
160     if (x > 1)
161         fac[tot++] = x;
162     x = a[id];
163     for (int i = 0; i < tot; i++)
164     {
165         int cur = x / fac[i];
166         if (pos[cur])
167         {
168             G[id].emplace_back(pos[cur]);
169             G[pos[cur]].emplace_back(id);
170         }
171     }
172 }
173 int main(int argc, char const *argv[])
174 {
175     init();
176     int t;
177     // scanf("%d", &t);
178     read(t);
179     while (t--)
180     {
181         read(n);
182         // scanf("%d", &n);
183         pos.clear();
184         for (int i = 1; i <= n; i++)
185         {
186             read(a[i]);
187             // scanf("%d", &a[i]);
188             pos[a[i]] = i;
189             G[i].clear();
190         }
191         for (int i = 1; i <= n; i++)
192         {
193             add(a[i], i);
194         }
195         uN = n;
196         printf("Case %d: %d
", tot++, n - MaxMatch() / 2);
197     }
198     return 0;
199 }

View Code

C - Aladdin and the Flying Carpet

Description

每次查询给出两个数n，a，求出所有的满足(i<j,i*j=n，且min(i,j)>=a)的数对个数

Solution

由唯一分解定理可以知道一个正整数n可以唯一分解为n=(p₁^^r₁)*(p₂^^r_2...),其所有约数个数为q=(1+r1)*(1+r2)...,那么约数个数q/2就是所有满足i*j=n的个数，注意到题上说是长方形而非正方形，可以不用考虑完全平方数+1的情况，

然后需要min(i,j)>=b,我们把小于b的约数剪掉即是答案

  1 //唯一分解定理
  2 //我们知道对于一个正整数n可以分解为n=(p0^a0)*(p1^a1)*...,p为素因子
  3 //这时正整数n的约数个数就是(1+a0)*(1+a1)*(1+a2)*(1+a3)...
  4 //对于此题，我们可以先用欧拉筛筛出前sqrt（max(a))的数，然后求出约数个数，
  5 //约数个数/2即为全部的整数对（i，j)满足i*j=a
  6 //要使min(i,j)>=b
  7 //我们只需要将前b个自然数中的约数个数剪掉即可
  8 //长方形而非正方形，不用考虑完全平方数加1的情况
  9 #include <bits/stdc++.h>
 10 #define lson rt << 1, l, mid
 11 #define rson rt << 1 | 1, mid + 1, r
 12 using namespace std;
 13 using ll = long long;
 14 using ull = unsigned long long;
 15 using pa = pair<int, int>;
 16 using ld = long double;
 17 ll n, m, k;
 18 const int maxn = 1e6 + 10;
 19 const int mod = 998244353;
 20 template <class T>
 21 inline T read(T &ret)
 22 {
 23     int f = 1;
 24     ret = 0;
 25     char ch = getchar();
 26     while (!isdigit(ch))
 27     {
 28         if (ch == '-')
 29             f = -1;
 30         ch = getchar();
 31     }
 32     while (isdigit(ch))
 33     {
 34         ret = (ret << 1) + (ret << 3) + ch - '0';
 35         ch = getchar();
 36     }
 37     ret *= f;
 38     return ret;
 39 }
 40 template <class T>
 41 inline void write(T n)
 42 {
 43     if (n < 0)
 44     {
 45         putchar('-');
 46         n = -n;
 47     }
 48     if (n >= 10)
 49     {
 50         write(n / 10);
 51     }
 52     putchar(n % 10 + '0');
 53 }
 54 ll prime[maxn];
 55 int vis[maxn];
 56 int cnt = 0;
 57 void init() //欧拉筛
 58 {
 59     for (int i = 2; i < maxn; i++)
 60     {
 61         if (!vis[i])
 62             prime[cnt++] = i;
 63         for (int j = 0; j < cnt && prime[j] * i < maxn; j++)
 64         {
 65             vis[prime[j] * i] = 1;
 66             if (i % prime[j] == 0)
 67                 break;
 68         }
 69     }
 70 }
 71 int main(int argc, char const *argv[])
 72 {
 73     init();
 74     int t;
 75     read(t);
 76     int tot = 0;
 77     while (t--)
 78     {
 79         ll a, b;
 80         read(a);
 81         read(b);
 82         int ans = 0;
 83         if (b * b <= a)
 84         {
 85             ll tmp = a;
 86             ans = 1;
 87             for (int i = 0; i < cnt && prime[i] <= sqrt(tmp); i++)
 88             {
 89                 if (tmp % prime[i] == 0)
 90                 {
 91                     int cur = 0;
 92                     while (tmp % prime[i] == 0)
 93                     {
 94                         ++cur;
 95                         tmp /= prime[i];
 96                     }
 97                     ans *= (1 + cur);
 98                 }
 99             }
100             if (tmp > 1)
101                 ans <<= 1;
102             // if (ans & 1)
103             //     ++ans;
104             ans >>= 1;
105             for (int i = 1; i < b; i++)
106                 if (a % i == 0)
107                     --ans;
108         }
109         printf("Case %d: %d
", ++tot, ans);
110     }
111     return 0;
112 }

View Code

D - Sigma Function

Description

给定一个自然数n，求出小于n的自然数有多少个的约数之和为偶数，输出数量

Solution

n=(p₁^^r₁)*(p₂^^r_2...)，约数之和a=(1+p1+p1^2+..p1^r1)*(1+p2+p2^2+..p2^2)....，等比求和即可得到原题式子（然而我并不会用这个推出结论，还是打表来的）

打表找规律，发现为约数和为奇数的数字为完全平方数或者2倍完全平方数，减去即可

  1 //一个数所有因子和为(1+p1+p1^2+...+p1^e1)*(1+p2+p2^2+...p2^e2)*...()
  2 //打表发现因子和为奇数的数是平方数或2倍平方数
  3 //减去即可
  4 //注意sqrt返回值为浮点数，需要转换为ll，不然double/float转ll会丢失精度，就wa
  5 #include <bits/stdc++.h>
  6 #define lson rt << 1, l, mid
  7 #define rson rt << 1 | 1, mid + 1, r
  8 using namespace std;
  9 using ll = long long;
 10 using ull = unsigned long long;
 11 using pa = pair<int, int>;
 12 using ld = long double;
 13 ll n, m, k;
 14 const ll maxn = 1e6;
 15 const int mod = 998244353;
 16 template <class T>
 17 inline T read(T &ret)
 18 {
 19     int f = 1;
 20     ret = 0;
 21     char ch = getchar();
 22     while (!isdigit(ch))
 23     {
 24         if (ch == '-')
 25             f = -1;
 26         ch = getchar();
 27     }
 28     while (isdigit(ch))
 29     {
 30         ret = (ret << 1) + (ret << 3) + ch - '0';
 31         ch = getchar();
 32     }
 33     ret *= f;
 34     return ret;
 35 }
 36 template <class T>
 37 inline void write(T n)
 38 {
 39     if (n < 0)
 40     {
 41         putchar('-');
 42         n = -n;
 43     }
 44     if (n >= 10)
 45     {
 46         write(n / 10);
 47     }
 48     putchar(n % 10 + '0');
 49 }
 50 ll prime[maxn];
 51 int vis[maxn];
 52 int pcnt = 0;
 53 void init() //欧拉筛
 54 {
 55     for (int i = 2; i < maxn; i++)
 56     {
 57         if (!vis[i])
 58             prime[pcnt++] = i;
 59         for (int j = 0; j < pcnt && prime[j] * i < maxn; j++)
 60         {
 61             vis[prime[j] * i] = 1;
 62             if (i % prime[j] == 0)
 63                 break;
 64         }
 65     }
 66 }
 67 ll cal(int p, int n)
 68 {
 69     ll sum = 1;
 70     ll t = 1;
 71     for (int i = 0; i < n; i++)
 72     {
 73         t *= p;
 74         sum += t;
 75     }
 76     // cout << "sum"
 77     //      << " :" << p << " " << n << " " << sum << "
";
 78     return sum;
 79 }
 80 int getFacSum(int x)
 81 {
 82     ll sum = 1;
 83     for (int i = 0; i < pcnt && prime[i] * prime[i] <= x; i++)
 84     {
 85         int p = prime[i];
 86         int cur = 0;
 87         while (x % p == 0)
 88         {
 89             ++cur;
 90             x /= p;
 91         }
 92         ll t = cal(p, cur);
 93         sum *= t;
 94     }
 95     if (x > 1)
 96         sum *= cal(x, 1);
 97     return sum;
 98 }
 99 void dabiao()
100 {
101     for (int i = 1; i <= 100; i++)
102         // getFacSum(i);
103         if (getFacSum(i) & 1)
104             cout << i << ": " << getFacSum(i) << "
";
105 }
106 int main(int argc, char const *argv[])
107 {
108     init();
109     int t;
110     // dabiao();
111     read(t);
112     int tot = 0;
113     while (t--)
114     {
115         ll x;
116         read(x);
117         ll ans = x;
118         ans = ans - (ll)sqrt(x) - (ll)sqrt(x / 2);
119         printf("Case %d: %lld
", ++tot, ans);
120     }
121     return 0;
122 }

View Code

E - Leading and Trailing

Description

给出一个数以及其幂指数，求出最终结果的前三位和后三位

Solution

对于后三位，直接快速幂即可，高于三位截断

对于前三位其实也阔以这样，不过需要用double（或ld）记录当前答案，不然wa（雾）

  1 //低位直接算，大于1000就截掉
  2 //高位思想类似，不过需要用double，不然得不到答案(雾)
  3 #include <bits/stdc++.h>
  4 #define lson rt << 1, l, mid
  5 #define rson rt << 1 | 1, mid + 1, r
  6 using namespace std;
  7 using ll = long long;
  8 using ull = unsigned long long;
  9 using pa = pair<int, int>;
 10 using ld = long double;
 11 ll n, m, k;
 12 const ll maxn = 1e6;
 13 const int mod = 998244353;
 14 template <class T>
 15 inline T read(T &ret)
 16 {
 17     int f = 1;
 18     ret = 0;
 19     char ch = getchar();
 20     while (!isdigit(ch))
 21     {
 22         if (ch == '-')
 23             f = -1;
 24         ch = getchar();
 25     }
 26     while (isdigit(ch))
 27     {
 28         ret = (ret << 1) + (ret << 3) + ch - '0';
 29         ch = getchar();
 30     }
 31     ret *= f;
 32     return ret;
 33 }
 34 template <class T>
 35 inline void write(T n)
 36 {
 37     if (n < 0)
 38     {
 39         putchar('-');
 40         n = -n;
 41     }
 42     if (n >= 10)
 43     {
 44         write(n / 10);
 45     }
 46     putchar(n % 10 + '0');
 47 }
 48 int qpow2(ll a, int b)
 49 {
 50     int c = 1000;
 51     a %= c;
 52     int ans = 1;
 53     while (b)
 54     {
 55         if (b & 1)
 56         {
 57             ans *= a;
 58             if (ans >= c)
 59                 ans %= c;
 60         }
 61         a *= a;
 62         if (a >= c)
 63             a %= c;
 64         b >>= 1;
 65     }
 66     return ans;
 67 }
 68 int qpow1(ld a, int b)
 69 {
 70     ll c = 1e4;
 71     ld ans = 1; //ll会wa
 72     while (b)
 73     {
 74         if (b & 1)
 75         {
 76             ans *= a;
 77             while (ans >= c)
 78                 ans /= 10;
 79         }
 80         a *= a;
 81         while (a >= c)
 82             a /= 10;
 83         b >>= 1;
 84     }
 85     while (ans >= 1000)
 86     {
 87         ans /= 10;
 88     }
 89     return (int)ans;
 90 }
 91 int main(int argc, char const *argv[])
 92 {
 93     int t;
 94     int tot = 0;
 95     read(t);
 96     while (t--)
 97     {
 98         ll n;
 99         int k;
100         read(n), read(k);
101         ll ff = n;
102         int fa = qpow1(ff, k);
103         ll llt = n;
104         int la = qpow2(llt, k);
105         printf("Case %d: %d %03d
", ++tot, fa, la);
106     }
107     return 0;
108 }

View Code

F - Goldbach`s Conjecture

Description

验证哥德巴赫猜想，给一个大于2的偶数n，找出有多少个素数对a,b满足(a<=b,a+b=n),输出个数

Solution

素数打表到1e7，对于每个查询暴力查询到n/2，记录答案

注意内存限制，需要将标记数组设为short或者bool，prime数组开到1e6即可

 1 //素数筛
 2 //处理到n/2即可
 3 #include <bits/stdc++.h>
 4 #define lson rt << 1, l, mid
 5 #define rson rt << 1 | 1, mid + 1, r
 6 using namespace std;
 7 using ll = long long;
 8 using ull = unsigned long long;
 9 using pa = pair<int, int>;
10 using ld = long double;
11 ll n, m, k;
12 const int maxn = 1e7 + 1000;
13 const int mod = 998244353;
14 template <class T>
15 inline T read(T &ret)
16 {
17     int f = 1;
18     ret = 0;
19     char ch = getchar();
20     while (!isdigit(ch))
21     {
22         if (ch == '-')
23             f = -1;
24         ch = getchar();
25     }
26     while (isdigit(ch))
27     {
28         ret = (ret << 1) + (ret << 3) + ch - '0';
29         ch = getchar();
30     }
31     ret *= f;
32     return ret;
33 }
34 template <class T>
35 inline void write(T n)
36 {
37     if (n < 0)
38     {
39         putchar('-');
40         n = -n;
41     }
42     if (n >= 10)
43     {
44         write(n / 10);
45     }
46     putchar(n % 10 + '0');
47 }
48 int pcnt, prime[maxn / 10];
49 short vis[maxn];
50 void init()
51 {
52     vis[0] = vis[1] = 1;
53     for (int i = 2; i < maxn; i++)
54     {
55         if (!vis[i])
56             prime[pcnt++] = i;
57         for (int j = 0; j < pcnt && prime[j] * i < maxn; j++)
58         {
59             vis[prime[j] * i] = 1;
60             if (i % prime[j] == 0)
61                 break;
62         }
63     }
64 }
65 int solve(int n)
66 {
67     int ans = 0;
68     for (int i = 0; i < pcnt && prime[i] <= n / 2; i++)
69     {
70         if (!vis[n - prime[i]])
71             ++ans;
72     }
73     return ans;
74 }
75 int main(int argc, char const *argv[])
76 {
77     init();
78     int t;
79     scanf("%d", &t);
80     int tot = 0;
81     while (t--)
82     {
83         int n;
84         // read(n);
85         scanf("%d", &n);
86         printf("Case %d: %d
", ++tot, solve(n));
87     }
88     return 0;
89 }

View Code

G - Harmonic Number (II)

Description

整数分块儿

Solution

对于一个数x，[n/x,n/(n/x)]的值都是n/x,由此暴力即可

 1 //整数分块儿
 2 #include <bits/stdc++.h>
 3 #define lson rt << 1, l, mid
 4 #define rson rt << 1 | 1, mid + 1, r
 5 using namespace std;
 6 using ll = long long;
 7 using ull = unsigned long long;
 8 using pa = pair<int, int>;
 9 using ld = long double;
10 ll n, m, k;
11 const int maxn = 1e7 + 1000;
12 const int mod = 998244353;
13 template <class T>
14 inline T read(T &ret)
15 {
16     int f = 1;
17     ret = 0;
18     char ch = getchar();
19     while (!isdigit(ch))
20     {
21         if (ch == '-')
22             f = -1;
23         ch = getchar();
24     }
25     while (isdigit(ch))
26     {
27         ret = (ret << 1) + (ret << 3) + ch - '0';
28         ch = getchar();
29     }
30     ret *= f;
31     return ret;
32 }
33 template <class T>
34 inline void write(T n)
35 {
36     if (n < 0)
37     {
38         putchar('-');
39         n = -n;
40     }
41     if (n >= 10)
42     {
43         write(n / 10);
44     }
45     putchar(n % 10 + '0');
46 }
47 ll solve(ll n)
48 {
49     ll ans = n + n / 2;
50     for (ll i = 3; i <= n;)
51     {
52         ll to = n / (n / i);
53         ans += (n / i) * (to - i + 1);
54         i = to + 1;
55     }
56     return ans;
57 }
58 int main(int argc, char const *argv[])
59 {
60     int t;
61     read(t);
62     int tot = 0;
63     while (t--)
64     {
65         int n;
66         read(n);
67         printf("Case %d: %lld
", ++tot, solve(n));
68     }
69     return 0;
70 }

View Code

H - Pairs Forming LCM

Description

Solution

由唯一分解定理知，一个数n可以唯一分解为n=(p₁^r₁)*(p₂^r_2...),

假设只有一个质因子p1，指数为r1，则[a,b]=n可以得到a,b的分解必有一个幂次为r1，剩下一个数的幂次可以0，r1任选，一共C(2,1)*(r1+1)种情况，

不过两者都是r1的时候算重叠了，需要减去，则此时对答案的贡献就是2*r1+1，考虑分步原理，每个质因子对答案的贡献都是如此计算，则计算出来ans=(2*r1+1)*(2*r2+1)...

不过由于我们不仅仅计算了，a<b,也计算了a>b,这时候需要将答案除以2，为什么没有考虑a==b呢，因为只有a=b=n这一种情况可以对答案有贡献，最后再加上1即是答案

  1 /* 
  2 唯一分解定理
  3 lcm(a,b)=n,则
  4 n=p1^r1*p2^r2...pm^rm
  5 a=p1^a1*p2^a2...pm^am
  6 b=p1^b1*p2^b2...pm^bm
  7 对于每一个ri都有ai+bi=ri，且ai，bi必须有一个为ri
  8 所以一个ri对应有2(ri+1),(从0开始)种贡献，不过当ai=bi=ri时算了两次，应减去
  9 因此最终每一个素因子对答案的贡献就是2*(ri+1)-1=2*ri+1
 10 根据分步原理ans=PI(2*ri+1)
 11 计算完毕后，我们可以直到，对于所有的a，b我们计算了a>=b和a<b的情况（除了最后a=b=n),即求出的是答案的二倍
 12 因此最后答案是ans=ans/2+1
 13 */
 14 
 15 #pragma optmize(3)
 16 #include <bits/stdc++.h>
 17 #define lson rt << 1, l, mid
 18 #define rson rt << 1 | 1, mid + 1, r
 19 using namespace std;
 20 using ll = long long;
 21 using ull = unsigned long long;
 22 using pa = pair<int, int>;
 23 using ld = long double;
 24 ll n, m, k;
 25 const int maxn = 1e7 + 1000;
 26 const int mod = 998244353;
 27 template <class T>
 28 inline T read(T &ret)
 29 {
 30     int f = 1;
 31     ret = 0;
 32     char ch = getchar();
 33     while (!isdigit(ch))
 34     {
 35         if (ch == '-')
 36             f = -1;
 37         ch = getchar();
 38     }
 39     while (isdigit(ch))
 40     {
 41         ret = (ret << 1) + (ret << 3) + ch - '0';
 42         ch = getchar();
 43     }
 44     ret *= f;
 45     return ret;
 46 }
 47 template <class T>
 48 inline void write(T n)
 49 {
 50     if (n < 0)
 51     {
 52         putchar('-');
 53         n = -n;
 54     }
 55     if (n >= 10)
 56     {
 57         write(n / 10);
 58     }
 59     putchar(n % 10 + '0');
 60 }
 61 int prime[maxn / 10];
 62 bool vis[maxn];
 63 int pcnt = 0;
 64 void init()
 65 {
 66     vis[0] = vis[1] = 1;
 67     for (int i = 2; i < maxn; i++)
 68     {
 69         if (!vis[i])
 70             prime[pcnt++] = i;
 71         for (int j = 0; j < pcnt && i * prime[j] < maxn; j++)
 72         {
 73             vis[prime[j] * i] = 1;
 74             if (i % prime[j] == 0)
 75                 break;
 76         }
 77     }
 78 }
 79 inline ll lcm(ll a, ll b)
 80 {
 81     ll g = __gcd(a, b);
 82     return a / g * b;
 83 }
 84 ll solve(ll c)
 85 {
 86     ll ans = 1;
 87     for (int i = 0; i < pcnt && prime[i] * prime[i] <= c; i++)
 88     {
 89         int cur = 0;
 90         while (c % prime[i] == 0)
 91         {
 92             c /= prime[i];
 93             ++cur;
 94         }
 95         if (cur)
 96             ans *= (2 * cur + 1);
 97     }
 98     if (c > 1)
 99         ans *= 3;
100     return ans / 2 + 1;
101 }
102 int main(int argc, char const *argv[])
103 {
104     init();
105     int t;
106     read(t);
107     int tot = 0;
108     while (t--)
109     {
110         ll n;
111         read(n);
112         printf("Case %d: %lld
", ++tot, solve(n));
113     }
114     return 0;
115 }

View Code

I - Harmonic Number

Description

给定一个整数n，求调和奇数h(n)

Solution

解法1：

记住公式h(n)=ln(n)+C+1/(2n),C为欧拉常数=0.57721566490153286060651209....（仅在数比较大时适用，较小时应采用累加方式计算）

解法2：

打表，可以看出h(n)是有累加性质的，我们每50项记录一个区间答案,即我们记录h(50),h(100),h(150)...

然后对于每个查询都可以在50次运算内找出答案

  1 /*
  2 h(n)≈ln(n)+C+1/(2*n) 
  3 C为欧拉常数=0.57721566490153286060651209
  4 仅在n比较大时适用
  5 
  6 也阔以打表分50个记录一个
  7  */
  8 // #pragma optmize(3)
  9 #include <bits/stdc++.h>
 10 #define lson rt << 1, l, mid
 11 #define rson rt << 1 | 1, mid + 1, r
 12 using namespace std;
 13 using ll = long long;
 14 using ull = unsigned long long;
 15 using pa = pair<int, int>;
 16 using ld = long double;
 17 ll n, m, k;
 18 const int maxn = 1e8 + 1;
 19 const double r = 0.57721566490153286060651209;
 20 const int mod = 998244353;
 21 template <class T>
 22 inline T read(T &ret)
 23 {
 24     int f = 1;
 25     ret = 0;
 26     char ch = getchar();
 27     while (!isdigit(ch))
 28     {
 29         if (ch == '-')
 30             f = -1;
 31         ch = getchar();
 32     }
 33     while (isdigit(ch))
 34     {
 35         ret = (ret << 1) + (ret << 3) + ch - '0';
 36         ch = getchar();
 37     }
 38     ret *= f;
 39     return ret;
 40 }
 41 template <class T>
 42 inline void write(T n)
 43 {
 44     if (n < 0)
 45     {
 46         putchar('-');
 47         n = -n;
 48     }
 49     if (n >= 10)
 50     {
 51         write(n / 10);
 52     }
 53     putchar(n % 10 + '0');
 54 }
 55 double a[10010];
 56 void init()
 57 {
 58     a[0] = 0;
 59     for (int i = 1; i <= 10000; i++)
 60         a[i] = a[i - 1] + 1.0 / i;
 61 }
 62 double h(int n)
 63 {
 64     if (n <= 10000)
 65         return a[n];
 66     return log(n) + r + 1 / (2.0 * n);
 67 }
 68 double ans[2000100];
 69 void dabiao()
 70 {
 71     double tmp = 1;
 72     for (int i = 2; i < maxn; i++)
 73     {
 74         tmp += 1.0 / i;
 75         if (i % 50 == 0)
 76             ans[i / 50] = tmp;
 77     }
 78 }
 79 double solve(int n)
 80 {
 81     int pre = n / 50;
 82     double a = ans[pre];
 83     pre *= 50;
 84     ++pre;
 85     for (; pre <= n; pre++)
 86         a += (ld)1.0 / pre;
 87     return a;
 88 }
 89 int main(int argc, char const *argv[])
 90 {
 91     // init();
 92     dabiao();
 93     int t;
 94     read(t);
 95     int tot = 0;
 96     while (t--)
 97     {
 98         int n;
 99         read(n);
100         printf("Case %d: %.10lf
", ++tot, solve(n));
101     }
102     return 0;
103 }

View Code

J - Mysterious Bacteria

Description

给出一个n，求一个a^b=n，使得b最大，输出最大的b

Solution

由唯一分解定理可知，要使n可以分解为a^b,b一定为(r1,r2,r3,..rn)。

如果n是负数，特判b是否为奇数，不是奇数b一直除以2

 1 //还有对于负数的处理
 2 //对于整数，ans=(r1,r2,...rn)
 3 //对于负数，先取相反数，然后如果ans为偶数，则一直/2直到不为偶数
 4 #include <bits/stdc++.h>
 5 #define lson rt << 1, l, mid
 6 #define rson rt << 1 | 1, mid + 1, r
 7 using namespace std;
 8 using ll = long long;
 9 using ull = unsigned long long;
10 using pa = pair<int, int>;
11 using ld = long double;
12 ll n, m, k;
13 const ll maxn = 1LL << 31;
14 const int mod = 998244353;
15 template <class T>
16 inline T read(T &ret)
17 {
18     int f = 1;
19     ret = 0;
20     char ch = getchar();
21     while (!isdigit(ch))
22     {
23         if (ch == '-')
24             f = -1;
25         ch = getchar();
26     }
27     while (isdigit(ch))
28     {
29         ret = (ret << 1) + (ret << 3) + ch - '0';
30         ch = getchar();
31     }
32     ret *= f;
33     return ret;
34 }
35 template <class T>
36 inline void write(T n)
37 {
38     if (n < 0)
39     {
40         putchar('-');
41         n = -n;
42     }
43     if (n >= 10)
44     {
45         write(n / 10);
46     }
47     putchar(n % 10 + '0');
48 }
49 int solve(ll n)
50 {
51     int ans = -1;
52     for (ll i = 2; i * i <= n; i++)
53     {
54         int cur = 0;
55         while (n % i == 0)
56         {
57             ++cur;
58             n /= i;
59         }
60         if (cur)
61         {
62             if (ans != -1)
63                 ans = __gcd(ans, cur);
64             else
65                 ans = cur;
66         }
67     }
68     if (n > 1)
69         ans = 1;
70     return ans;
71 }
72 int main(int argc, char const *argv[])
73 {
74     int t;
75     read(t);
76     int tot = 0;
77     while (t--)
78     {
79         ll n;
80         read(n);
81         int f = 0;
82         if (n < 0)
83         {
84             f = 1;
85             n = -n;
86         }
87         int ans = solve(n);
88         if (f)
89         {
90             while (ans % 2 == 0)
91                 ans /= 2;
92         }
93         printf("Case %d: %d
", ++tot, ans);
94     }
95     return 0;
96 }

View Code

K - Large Division

Description

给一个大整数n，一个小整数b，判断b能否整除a

Solution

高精度除以低精度，判读最后余数是否为0即可

 1 //高精/低精度
 2 #include <bits/stdc++.h>
 3 #define lson rt << 1, l, mid
 4 #define rson rt << 1 | 1, mid + 1, r
 5 using namespace std;
 6 using ll = long long;
 7 using ull = unsigned long long;
 8 using pa = pair<int, int>;
 9 using ld = long double;
10 ll n, m, k;
11 const ll maxn = 1LL << 31;
12 const int mod = 998244353;
13 template <class T>
14 inline T read(T &ret)
15 {
16     int f = 1;
17     ret = 0;
18     char ch = getchar();
19     while (!isdigit(ch))
20     {
21         if (ch == '-')
22             f = -1;
23         ch = getchar();
24     }
25     while (isdigit(ch))
26     {
27         ret = (ret << 1) + (ret << 3) + ch - '0';
28         ch = getchar();
29     }
30     ret *= f;
31     return ret;
32 }
33 template <class T>
34 inline void write(T n)
35 {
36     if (n < 0)
37     {
38         putchar('-');
39         n = -n;
40     }
41     if (n >= 10)
42     {
43         write(n / 10);
44     }
45     putchar(n % 10 + '0');
46 }
47 vector<int> a;
48 int b;
49 char ss[210];
50 int solve()
51 {
52     int sz = a.size();
53     ll t = 0; //注意这里当b为maxInt时,有可能超出int范围，所以应该用ll
54     for (int i = 0; i < sz; i++)
55     {
56         t = t * 10 + a[i];
57         t %= b;
58     }
59     return t == 0;
60 }
61 int main(int argc, char const *argv[])
62 {
63     int t;
64     scanf("%d", &t);
65     int tot = 0;
66     char s[2][20] = {"not divisible", "divisible"};
67     while (t--)
68     {
69         a.clear();
70         scanf("%s%d", ss, &b);
71         b = abs(b);
72         int len = strlen(ss);
73         if (ss[0] == '-')
74             for (int i = 1; i < len; i++)
75                 a.emplace_back(ss[i] - '0');
76         else
77             for (int i = 0; i < len; i++)
78                 a.emplace_back(ss[i] - '0');
79 
80         int ans = solve();
81         printf("Case %d: %s
", ++tot, s[ans]);
82     }
83     return 0;
84 }

View Code

L - Fantasy of a Summation

Description

依代码行事

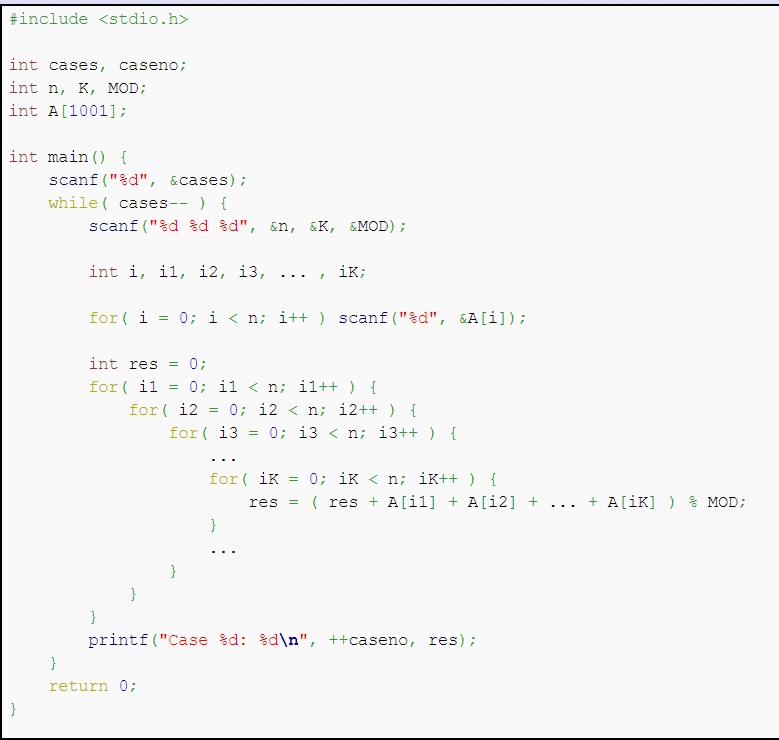
Solution

找规律发现序列每个数出现次数为n^(k-1)

快速幂

 1 // 找规律发现序列每个数出现次数为n^(k-1)
 2 // 快速幂即可
 3 #include <bits/stdc++.h>
 4 #define lson rt << 1, l, mid
 5 #define rson rt << 1 | 1, mid + 1, r
 6 using namespace std;
 7 using ll = long long;
 8 using ull = unsigned long long;
 9 using pa = pair<int, int>;
10 using ld = long double;
11 int n, m, k, mod;
12 const ll maxn = 1LL << 31;
13 template <class T>
14 inline T read(T &ret)
15 {
16     int f = 1;
17     ret = 0;
18     char ch = getchar();
19     while (!isdigit(ch))
20     {
21         if (ch == '-')
22             f = -1;
23         ch = getchar();
24     }
25     while (isdigit(ch))
26     {
27         ret = (ret << 1) + (ret << 3) + ch - '0';
28         ch = getchar();
29     }
30     ret *= f;
31     return ret;
32 }
33 template <class T>
34 inline void write(T n)
35 {
36     if (n < 0)
37     {
38         putchar('-');
39         n = -n;
40     }
41     if (n >= 10)
42     {
43         write(n / 10);
44     }
45     putchar(n % 10 + '0');
46 }
47 int qpow(int a, int b)
48 {
49     int ans = 1;
50     while (b)
51     {
52         if (b & 1)
53             ans = ans * a % mod;
54         a = a * a % mod;
55         b >>= 1;
56     }
57     return ans;
58 }
59 int a[1010];
60 ll solve()
61 {
62     ll ans = 0;
63     ll p = (qpow(n, k - 1) * (k % mod)) % mod;
64     for (int i = 0; i < n; i++)
65         ans = (ans + p * a[i] % mod) % mod;
66     return ans;
67 }
68 int main(int argc, char const *argv[])
69 {
70     int t;
71     read(t);
72     int tot = 0;
73     while (t--)
74     {
75         read(n), read(k), read(mod);
76         for (int i = 0; i < n; i++)
77             read(a[i]);
78         printf("Case %d: %lld
", ++tot, solve());
79     }
80     return 0;
81 }

View Code

M - Help Hanzo

Description

给一个区间输出区间内由多少素数

Solution

区间素数筛

  1 /*
  2 区间素数筛板题
  3 注意a为1时需要减去1
  4  */
  5 #pragma optimize(3)
  6 #include <bits/stdc++.h>
  7 #define lson rt << 1, l, mid
  8 #define rson rt << 1 | 1, mid + 1, r
  9 using namespace std;
 10 using ll = long long;
 11 using ull = unsigned long long;
 12 using pa = pair<int, int>;
 13 using ld = long double;
 14 int n, m, k, mod;
 15 const int maxn = 1e5 + 10;
 16 template <class T>
 17 inline T read(T &ret)
 18 {
 19     int f = 1;
 20     ret = 0;
 21     char ch = getchar();
 22     while (!isdigit(ch))
 23     {
 24         if (ch == '-')
 25             f = -1;
 26         ch = getchar();
 27     }
 28     while (isdigit(ch))
 29     {
 30         ret = (ret << 1) + (ret << 3) + ch - '0';
 31         ch = getchar();
 32     }
 33     ret *= f;
 34     return ret;
 35 }
 36 template <class T>
 37 inline void write(T n)
 38 {
 39     if (n < 0)
 40     {
 41         putchar('-');
 42         n = -n;
 43     }
 44     if (n >= 10)
 45     {
 46         write(n / 10);
 47     }
 48     putchar(n % 10 + '0');
 49 }
 50 
 51 ll multiMod(ll a, ll b, ll mod)
 52 {
 53     ll ret = 0LL;
 54     a %= mod;
 55     while (b)
 56     {
 57         if (b & 1LL)
 58             ret = (ret + a) % mod, --b;
 59         b >>= 1LL;
 60         a = (a + a) % mod;
 61     }
 62     return ret;
 63 }
 64 
 65 bool isprime1[maxn], isprime2[maxn];
 66 int solve(ll a, ll b)
 67 {
 68     for (ll i = 0; i * i <= b; i++)
 69         isprime1[i] = 0;
 70     for (ll i = 0; i <= b - a; i++)
 71         isprime2[i] = 1;
 72     for (ll i = 2; i * i <= b; i++)
 73     {
 74         if (!isprime1[i])
 75         {
 76             for (ll j = i + i; j * j <= b; j += i)
 77                 isprime1[j] = 1;
 78             for (ll j = max(2LL, (a + i - 1) / i) * i; j <= b; j += i)
 79                 isprime2[j - a] = 0;
 80         }
 81     }
 82     int sum = 0;
 83     for (int i = 0; i <= b - a; i++)
 84         if (isprime2[i])
 85             sum++;
 86     if (a == 1)
 87         --sum;
 88     return sum;
 89 }
 90 int main(int argc, char const *argv[])
 91 {
 92     int t;
 93     read(t);
 94     int tot = 0;
 95     while (t--)
 96     {
 97         int a, b;
 98         read(a), read(b);
 99         printf("Case %d: %d
", ++tot, solve(a, b));
100     }
101     return 0;
102 }

View Code

N - Trailing Zeroes (III)

Description

给一个整数n，判断n!末尾0有多少个

Solution

n!末尾0的个数只与5这个素因子有关

有公式f(n,p)=f(n/p,p)+n/p,求n!内因子p的个数

打表可知出现n个0的情况在4*n+1以后，由此可以将区间确定在一个小范围

 1 /*
 2     n!末尾0的个数只与5这个素因子有关
 3     有公式f(n,p)=f(n/p,p)+n/p,求n!内因子p的个数
 4     打表可知出现n个0的情况在4*n+1以后，由此可以将区间确定在一个小范围
 5  */
 6 #pragma optimize(3)
 7 #include <bits/stdc++.h>
 8 #define lson rt << 1, l, mid
 9 #define rson rt << 1 | 1, mid + 1, r
10 using namespace std;
11 using ll = long long;
12 using ull = unsigned long long;
13 using pa = pair<int, int>;
14 using ld = long double;
15 int n, m, k, mod;
16 const int maxn = 1e5 + 10;
17 template <class T>
18 inline T read(T &ret)
19 {
20     int f = 1;
21     ret = 0;
22     char ch = getchar();
23     while (!isdigit(ch))
24     {
25         if (ch == '-')
26             f = -1;
27         ch = getchar();
28     }
29     while (isdigit(ch))
30     {
31         ret = (ret << 1) + (ret << 3) + ch - '0';
32         ch = getchar();
33     }
34     ret *= f;
35     return ret;
36 }
37 template <class T>
38 inline void write(T n)
39 {
40     if (n < 0)
41     {
42         putchar('-');
43         n = -n;
44     }
45     if (n >= 10)
46     {
47         write(n / 10);
48     }
49     putchar(n % 10 + '0');
50 }
51 ull f(ull n, int p)
52 {
53     if (n == 0)
54         return 0;
55     return f(n / p, p) + n / p;
56 }
57 ull solve(ull n, int p)
58 {
59     for (ull i = 4 * n + 1;; i++)
60     {
61         if (f(i, p) == n)
62             return i;
63         if (f(i, p) > n)
64             return 0;
65     }
66 }
67 int main(int argc, char const *argv[])
68 {
69     int t;
70     read(t);
71     int tot = 0;
72     while (t--)
73     {
74         ull a;
75         read(a);
76         ull ans = solve(a, 5);
77         if (!ans)
78             printf("Case %d: impossible
", ++tot);
79         else
80             printf("Case %d: %llu
", ++tot, ans);
81     }
82     return 0;
83 }

View Code

O - GCD - Extreme (II)

Description

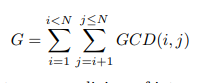
给N，求G

Solution

可以从题意得知满足答案满足一个递推关系

r[n]=r[n-1]+f(n),f(n)=(1,n)+(2,n)+...+(n-1,n)

对于f(n)如何求解呢，假设(x,n)=i,则有关系(x/i,n/i)=1

x<n,则x/i<n/i，即我们需要求小于n/i的数中与n/i互素的数个数，即phi(n/i)

那么这一组数对f(n)的贡献就为phi(n/i)*i

循环暴力gcd所有可能情况即可

循环推出r数组，o(1)查询

 1 #pragma optimize(3)
 2 #include <bits/stdc++.h>
 3 #define lson rt << 1, l, mid
 4 #define rson rt << 1 | 1, mid + 1, r
 5 using namespace std;
 6 using ll = long long;
 7 using ull = unsigned long long;
 8 using pa = pair<int, int>;
 9 using ld = long double;
10 int n, m, k, mod;
11 const int maxn = 4e6 + 10;
12 template <class T>
13 inline T read(T &ret)
14 {
15     int f = 1;
16     ret = 0;
17     char ch = getchar();
18     while (!isdigit(ch))
19     {
20         if (ch == '-')
21             f = -1;
22         ch = getchar();
23     }
24     while (isdigit(ch))
25     {
26         ret = (ret << 1) + (ret << 3) + ch - '0';
27         ch = getchar();
28     }
29     ret *= f;
30     return ret;
31 }
32 template <class T>
33 inline void write(T n)
34 {
35     if (n < 0)
36     {
37         putchar('-');
38         n = -n;
39     }
40     if (n >= 10)
41     {
42         write(n / 10);
43     }
44     putchar(n % 10 + '0');
45 }
46 int phi[maxn];
47 ull r[maxn], a[maxn];
48 void init()
49 {
50     for (int i = 1; i < maxn; i++)
51         phi[i] = i;
52     for (int i = 2; i < maxn; i++)
53     {
54         if (phi[i] == i)
55             for (int j = i; j < maxn; j += i)
56                 phi[j] = phi[j] / i * (i - 1);
57     }
58     for (int i = 1; i < maxn; i++)
59         for (int j = 2 * i; j < maxn; j += i)
60             a[j] += (ull)phi[j / i] * i;
61     for (int i = 2; i < maxn; i++)
62         r[i] = r[i - 1] + a[i];
63 }
64 inline ull solve(int n)
65 {
66     return r[n];
67 }
68 int main(int argc, char const *argv[])
69 {
70     init();
71     while (read(n))
72     {
73         write(solve(n));
74         putchar('
');
75     }
76     return 0;
77 }

View Code

P - Code Feat

Description

给出q组同余方程，求出自小的p个解，一个值满足一组方程内的一个即可，保证除数互素

Solution

同余方程组！除数互素！中国剩余定理，gkd！不对劲儿，冷静思考

首先我们思考普通情况我们有K=k1*k2*...*kn种同余方程组合

如果K很大那么用孙子定理/中国剩余定理是很慢的，这时候我们可以考虑暴力枚举

暴力枚举的话我们选定一个x最大的和一个k值最小的来枚举，why

这样我们每次的增量最大而且k值更小的话对于一次增量x来说需要循环判定次数最少，保证了复杂度

要选择最大的x和最小的k的组合可以采用kc/xc<ki/xi => kc*xi<xc*ki避免除法运算不正确

如果K比较小那么可以用孙子定理求解(注意到题目说了m互质，用最简单的版本即可)

  1 #pragma optimize(3)
  2 #include <bits/stdc++.h>
  3 #define lson rt << 1, l, mid
  4 #define rson rt << 1 | 1, mid + 1, r
  5 using namespace std;
  6 using ll = long long;
  7 using ull = unsigned long long;
  8 using pa = pair<int, int>;
  9 using ld = long double;
 10 const int maxn = 210;
 11 template <class T>
 12 inline T read(T &ret)
 13 {
 14     int f = 1;
 15     ret = 0;
 16     char ch = getchar();
 17     while (!isdigit(ch))
 18     {
 19         if (ch == '-')
 20             f = -1;
 21         ch = getchar();
 22     }
 23     while (isdigit(ch))
 24     {
 25         ret = (ret << 1) + (ret << 3) + ch - '0';
 26         ch = getchar();
 27     }
 28     ret *= f;
 29     return ret;
 30 }
 31 template <class T>
 32 inline void write(T n)
 33 {
 34     if (n < 0)
 35     {
 36         putchar('-');
 37         n = -n;
 38     }
 39     if (n >= 10)
 40     {
 41         write(n / 10);
 42     }
 43     putchar(n % 10 + '0');
 44 }
 45 int limit = 10000;
 46 unordered_set<int> se[maxn];
 47 int m[maxn], y[maxn][maxn], k[maxn], b[maxn];
 48 vector<int> res;
 49 int c, s;
 50 ll exgcd(ll a, ll b, ll &x, ll &y) //求逆元
 51 {
 52     if (b == 0)
 53     {
 54         x = 1, y = 0;
 55         return a;
 56     }
 57     ll ret = exgcd(b, a % b, y, x);
 58     y -= (a / b) * x;
 59     return ret;
 60 }
 61 
 62 ll crt()
 63 {
 64     ll d, x, y, ret = 0;
 65     ll temp;
 66     ll M = 1;
 67     for (int i = 0; i < c; i++)
 68         M *= m[i]; //m是除数
 69     for (int i = 0; i < c; i++)
 70     {
 71         temp = M / m[i];
 72         d = exgcd(m[i], temp, x, y);       //求temp在模mi意义下的逆元
 73         ret = (ret + y * temp * b[i]) % M; //b是余数
 74     }
 75     return (ret + M) % M;
 76 }
 77 void dfs(int dep)
 78 {
 79     if (dep == c)
 80     {
 81         res.emplace_back(crt());
 82         return;
 83     }
 84     for (int j = 0; j < k[dep]; j++)
 85     {
 86         b[dep] = y[dep][j];
 87         dfs(dep + 1);
 88     }
 89 }
 90 void solveCrt()
 91 {
 92     dfs(0);
 93     ll lcm = 1;
 94     sort(res.begin(), res.end());
 95     for (int i = 0; i < c; i++)
 96         lcm *= m[i];
 97     for (int i = 0; s; i++)
 98     {
 99         int sz = res.size();
100         for (int j = 0; j < sz && s; j++)
101         {
102             ll now = lcm * i + res[j];
103             if (now > 0)
104             {
105                 write(now);
106                 puts("");
107                 --s;
108             }
109         }
110     }
111 }
112 void solveEnum(int best)
113 {
114     for (int i = 0; i < c; i++)
115     {
116         if (i == best)
117             continue;
118         se[i].clear();
119         for (int j = 0; j < k[i]; j++)
120             se[i].insert(y[i][j]);
121     }
122     for (int i = 0; s; i++)
123         for (int j = 0; j < k[best] && s; j++)
124         {
125             ll now = m[best] * i + y[best][j];
126             if (!now)
127                 continue;
128             int f = 1;
129             for (int p = 0; p < c; p++)
130             {
131                 if (p != best && !se[p].count(now % m[p]))
132                 {
133                     f = 0;
134                     break;
135                 }
136             }
137             if (f)
138             {
139                 write(now);
140                 puts("");
141                 --s;
142             }
143         }
144 }
145 int main(int argc, char const *argv[])
146 {
147     while (read(c) && read(s))
148     {
149         res.clear();
150         int best = 0, tot = 1;
151         for (int i = 0; i < c; i++)
152         {
153             read(m[i]), read(k[i]);
154             for (int j = 0; j < k[i]; j++)
155                 read(y[i][j]);
156             sort(y[i], y[i] + k[i]);
157             if (m[best] * k[i] < m[i] * k[best])
158                 best = i;
159             tot *= k[i];
160         }
161         if (tot >= limit)
162             solveEnum(best);
163         else
164             solveCrt();
165         puts("");
166     }
167     return 0;
168 }

View Code

Q - Emoogle Grid

Description

给出一个n*m迷宫，k种颜色，里面有p个点不能染色，上下相邻的点不能是相同颜色，在mod 100000007的条件下的染色方案有res种，

m，k，p，res已知，求最小的n

Solution

先将不可变部分找出来，注意在题目给定的可见区域的下一行也是一定的，也算不可变区域

然后就得到一个式子(k-1)^(nx)*cur=res(mod 1e8+7),其中cur为已经求得种类数目，res是题目给定

然后利用乘法逆元将cur除到右边，再利用大步小步算法离散对数取模得到x值，将x值加上之前求得的行数即为答案

该用mod就用mod，别xjb用-。

  1 #include <bits/stdc++.h>
  2 #define lson rt << 1, l, mid
  3 #define rson rt << 1 | 1, mid + 1, r
  4 using namespace std;
  5 using ll = long long;
  6 using ull = unsigned long long;
  7 using pa = pair<int, int>;
  8 using ld = long double;
  9 const int maxn = 5100;
 10 const int mod = 100000007;
 11 ll n, k, m, pre, r;
 12 template <class T>
 13 inline T read(T &ret)
 14 {
 15     int f = 1;
 16     ret = 0;
 17     char ch = getchar();
 18     while (!isdigit(ch))
 19     {
 20         if (ch == '-')
 21             f = -1;
 22         ch = getchar();
 23     }
 24     while (isdigit(ch))
 25     {
 26         ret = (ret << 1) + (ret << 3) + ch - '0';
 27         ch = getchar();
 28     }
 29     ret *= f;
 30     return ret;
 31 }
 32 template <class T>
 33 inline void write(T n)
 34 {
 35     if (n < 0)
 36     {
 37         putchar('-');
 38         n = -n;
 39     }
 40     if (n >= 10)
 41     {
 42         write(n / 10);
 43     }
 44     putchar(n % 10 + '0');
 45 }
 46 ll qpow(ll a, ll b)
 47 {
 48     ll res = 1;
 49     while (b)
 50     {
 51         if (b & 1)
 52         {
 53             res = res * a % mod;
 54         }
 55         a = a * a % mod;
 56         b >>= 1;
 57     }
 58     return res;
 59 }
 60 struct node
 61 {
 62     ll x, y;
 63 } s[maxn];
 64 bool cmp(node a, node b)
 65 {
 66     if (a.y == b.y)
 67         return a.x < b.x;
 68     else
 69         return a.y < b.y;
 70 }
 71 inline void exgcd(ll a, ll b, ll &x, ll &y)
 72 {
 73     if (b != 0)
 74     {
 75         exgcd(b, a % b, y, x);
 76         y -= (a / b) * x;
 77     }
 78     else
 79     {
 80         x = 1, y = 0;
 81     }
 82 }
 83 
 84 inline ll inv(ll a)
 85 {
 86     return qpow(a, mod - 2);
 87 }
 88 ll BSGS(ll a, ll b)
 89 {
 90     ll m = (ll)sqrt(mod + 0.5);
 91     map<ll, ll> x;
 92     x[1] = 0;
 93     ll ans = 1;
 94     for (int i = 1; i <= m; i++)
 95     {
 96         ans = ans * a % mod;
 97         if (!x.count(ans))
 98             x[ans] = i;
 99     }
100     ll pm = inv(qpow(a, m));
101     for (int i = 0; i < m; i++)
102     {
103         if (x.count(b))
104             return i * m + x[b];
105         b = b * pm % mod;
106     }
107     return -1;
108 }
109 ll solve()
110 {
111     ll cur = 1;
112     ll ans = 1;
113     ll k1 = n; //可以为k种选择的格子数目
114     for (int i = 0; i < m; i++)
115     {
116         if (s[i].x == 1)
117             k1--;
118         if (s[i].x != r)
119         {
120             if (i + 1 < m && s[i + 1].y == s[i].y)
121             {
122                 if (s[i].x + 1 != s[i + 1].x)
123                 {
124                     k1++;
125                 }
126             }
127             else
128                 k1++;
129         }
130     }
131     cur = cur * qpow(k, k1) % mod;
132     cur = cur * qpow(k - 1, n * r - k1 - m) % mod;
133     if (cur == pre)
134         return r;
135     k1 = 0;
136     for (int i = 0; i < m; i++)
137     {
138         if (s[i].x == r)
139             k1++;
140     }
141     cur = cur * qpow(k, k1) % mod;
142     cur = cur * qpow(k - 1, n - k1) % mod;
143     if (cur == pre)
144         return r + 1;
145     //开始可变全为k-1部分
146     pre *= inv(cur);
147     pre %= mod;
148     k = qpow(k - 1, n);
149     r += BSGS(k, pre);
150     return r + 1;
151 }
152 int main(int argc, char const *argv[])
153 {
154     int t;
155     read(t);
156     // scanf("%d", &t);
157     int tot = 0;
158     while (t--)
159     {
160         r = 1;
161         read(n), read(k), read(m), read(pre);
162         // scanf("%lld %lld %lld %lld", &n, &k, &m, &pre);
163         for (int i = 0; i < m; i++)
164         {
165             read(s[i].x), read(s[i].y);
166             // scanf("%d%d", &s[i].x, &s[i].y);
167             r = max(s[i].x, r);
168         }
169         sort(s, s + m, cmp);
170         printf("Case %d: %lld
", ++tot, solve());
171     }
172     return 0;
173 }

View Code

R - 青蛙的约会

Description

同余方程求解最小整数解

Solution

扩展欧几里得

 1 #include <cstdio>
 2 #include <iostream>
 3 #define lson rt << 1, l, mid
 4 #define rson rt << 1 | 1, mid + 1, r
 5 using namespace std;
 6 typedef long long ll;
 7 const int maxn = 5100;
 8 const int mod = 100000007;
 9 ll n, k, m, pre, r;
10 void swap(ll &a, ll &b)
11 {
12     ll t = a;
13     a = b;
14     b = t;
15 }
16 ll exgcd(ll a, ll b, ll &x, ll &y)
17 {
18     if (!b)
19     {
20         x = 1, y = 0;
21         return a;
22     }
23     ll d = exgcd(b, a % b, y, x);
24     y -= (a / b) * x;
25     return d;
26 }
27 int main(int argc, char const *argv[])
28 {
29     ll x, y, m, n, l;
30     // read(x), read(y), read(m), read(n), read(l);
31     scanf("%lld %lld %lld %lld %lld", &x, &y, &m, &n, &l);
32     char im[] = "Impossible";
33     if (m == n)
34     {
35         puts(im);
36     }
37     else
38     {
39         ll a = n - m, b = x - y;
40         ll xa, yl;
41         ll d = exgcd(a, l, xa, yl);
42         if (b % d != 0)
43         {
44             puts(im);
45         }
46         else
47         {
48             ll times = l / d;
49             xa *= (x - y) / d;                 //最终解
50             xa = (xa % times + times) % times; //最小非负整数解
51             printf("%lld
", xa);
52         }
53     }
54     return 0;
55 }

View Code

S - C Looooops

Description

给出A,B,C,以及其数据范围2^k,求执行多少次

Solution

同余方程求解最小整数解

 1 // #include <bits/stdc++.h>
 2 #include <cstdio>
 3 #include <iostream>
 4 #define lson rt << 1, l, mid
 5 #define rson rt << 1 | 1, mid + 1, r
 6 using namespace std;
 7 // using ll = long long;
 8 // using ull = unsigned long long;
 9 // using pa = pair<int, int>;
10 // using ld = long double;
11 typedef long long ll;
12 const int maxn = 5100;
13 const int mod = 100000007;
14 ll n, k, m, pre, r;
15 // template <class T>
16 // inline T read(T &ret)
17 // {
18 //     int f = 1;
19 //     ret = 0;
20 //     char ch = getchar();
21 //     while (!isdigit(ch))
22 //     {
23 //         if (ch == '-')
24 //             f = -1;
25 //         ch = getchar();
26 //     }
27 //     while (isdigit(ch))
28 //     {
29 //         ret = (ret << 1) + (ret << 3) + ch - '0';
30 //         ch = getchar();
31 //     }
32 //     ret *= f;
33 //     return ret;
34 // }
35 // template <class T>
36 // inline void write(T n)
37 // {
38 //     if (n < 0)
39 //     {
40 //         putchar('-');
41 //         n = -n;
42 //     }
43 //     if (n >= 10)
44 //     {
45 //         write(n / 10);
46 //     }
47 //     putchar(n % 10 + '0');
48 // }
49 ll exgcd(ll a, ll b, ll &x, ll &y)
50 {
51     if (!b)
52     {
53         x = 1, y = 0;
54         return a;
55     }
56     ll d = exgcd(b, a % b, y, x);
57     y -= (a / b) * x;
58     return d;
59 }
60 int main(int argc, char const *argv[])
61 {
62     ll a, b, c, k;
63     while (~scanf("%lld%lld%lld%lld", &a, &b, &c, &k) && (a + b + c + k))
64     {
65         k = 1LL << k;
66         ll t = c;
67         c = b - a;
68         a = t, b = k;
69         ll x, y;
70         ll d = exgcd(a, b, x, y);
71         if (c % d)
72         {
73             puts("FOREVER");
74             continue;
75         }
76         ll r = c / d;
77         x *= r;
78         ll ra = b / d;
79         x = (x % ra + ra) % ra;
80         printf("%lld
", x);
81     }
82     return 0;
83 }

View Code

T - Death to Binary?

Description

模拟题，实锤了

Solution

  1 #include <bits/stdc++.h>
  2 #define ll long long
  3 #define lson l, m, rt << 1
  4 #define rson m + 1, r, rt << 1 | 1
  5 using namespace std;
  6 
  7 char str1[50], str2[50];
  8 char a[50], b[50], c[50];
  9 int solve(char a[])
 10 {
 11     int k = 50;
 12     while (k >= 0 && a[k] == 0)
 13         k--;
 14     while (k >= 0)
 15     {
 16         if (a[k] >= 1)
 17         {
 18             while (k - 1 >= 0 && (a[k - 1] >= 1 && a[k] >= 1))
 19             {
 20                 a[k + 1]++, a[k]--, a[k - 1]--;
 21                 if (a[k] == 0)
 22                 {
 23                     k--;
 24                     break;
 25                 }
 26                 else if (a[k - 1] == 0)
 27                 {
 28                     k -= 2;
 29                     break;
 30                 }
 31             }
 32             if (k - 1 >= 0 && a[k - 1] == 0)
 33             {
 34                 while (a[k] >= 2)
 35                 {
 36                     if (k > 1)
 37                         a[k] -= 2, a[k + 1]++, a[k - 2]++;
 38                     else if (k == 1)
 39                         a[k] -= 2, a[k + 1]++, a[k - 1]++;
 40                     else
 41                     {
 42                         k--;
 43                         break;
 44                     }
 45                 }
 46                 k--;
 47             }
 48             else if (k >= 0)
 49                 k--;
 50         }
 51         else
 52             k--;
 53     }
 54     k = 0;
 55     while (k < 50 && a[k] == 0)
 56         k++;
 57     if (k == 0)
 58     {
 59         while (a[0] >= 2)
 60         {
 61             a[1]++;
 62             a[0] -= 2;
 63         }
 64     }
 65     while (k < 50)
 66     {
 67         if (a[k] >= 1)
 68         {
 69             while (k + 1 < 50 && (a[k + 1] >= 1 && a[k] >= 1))
 70             {
 71                 a[k + 2]++, a[k]--, a[k + 1]--;
 72                 if (a[k] == 0)
 73                 {
 74                     k++;
 75                     break;
 76                 }
 77                 else if (a[k + 1] == 0)
 78                 {
 79                     k += 2;
 80                     break;
 81                 }
 82             }
 83             if (k + 1 <= 50 && a[k + 1] == 0)
 84             {
 85                 while (a[k] >= 2)
 86                 {
 87                     if (k > 1)
 88                         a[k] -= 2, a[k + 1]++, a[k - 2]++;
 89                     else if (k == 1)
 90                         a[k] -= 2, a[k + 1]++, a[k - 1]++;
 91                     else
 92                     {
 93                         k++;
 94                         break;
 95                     }
 96                 }
 97                 k++;
 98             }
 99             else if (k + 1 > 50)
100                 k++;
101         }
102         else
103             k++;
104     }
105     k = 50;
106     while (k >= 0 && a[k] == 0)
107         k--;
108     return k;
109 }
110 
111 void print(int ka, int shu, int num)
112 {
113     if (num == 1)
114         printf("  ");
115     if (num == 2)
116         printf("+ ");
117     if (ka >= 0)
118     {
119         for (int i = 0; i < shu - ka; i++)
120             printf(" ");
121         for (int i = ka; i >= 0; i--)
122         {
123             if (num == 1)
124                 printf("%d", a[i]);
125             else if (num == 2)
126                 printf("%d", b[i]);
127         }
128     }
129     else
130     {
131         for (int i = 0; i < shu; i++)
132             printf(" ");
133         printf("0");
134     }
135     printf("
");
136 }
137 
138 void print1(int k, int num)
139 {
140     printf("  ");
141     if (num >= 0)
142     {
143         for (int i = num; i >= 0; i--)
144         {
145             if (k == 1)
146                 printf("-");
147             else
148                 printf("%d", c[i]);
149         }
150     }
151     else
152     {
153         if (k == 1)
154             printf("-");
155         else
156             printf("0");
157     }
158     printf("
");
159     if (k == 2)
160         printf("
");
161 }
162 
163 int main()
164 {
165     while (~scanf("%s%s", str1, str2))
166     {
167         memset(a, 0, sizeof a);
168         memset(b, 0, sizeof b);
169         memset(c, 0, sizeof c);
170         int k1 = strlen(str1), k2 = strlen(str2);
171         for (int i = 0; i < k1; i++)
172             a[i] = str1[k1 - 1 - i] - '0';
173         for (int i = 0; i < k2; i++)
174             b[i] = str2[k2 - 1 - i] - '0';
175         int ka = solve(a);
176         int kb = solve(b);
177         for (int i = 50; i >= 0; i--)
178             c[i] = a[i] + b[i];
179         int kc = solve(c);
180         int num = max(max(ka, kb), kc);
181         print(ka, num, 1);
182         print(kb, num, 2);
183         print1(1, num);
184         print1(2, num);
185     }
186 }

View Code

U - Primes

Description

给出一个数n，判断是否素数

Solution

直接搞

 1 // #include <bits/stdc++.h>
 2 #include <cmath>
 3 #include <cstdio>
 4 #include <iostream>
 5 #define lson rt << 1, l, mid
 6 #define rson rt << 1 | 1, mid + 1, r
 7 using namespace std;
 8 // using ll = long long;
 9 // using ull = unsigned long long;
10 // using pa = pair<int, int>;
11 // using ld = long double;
12 typedef long long ll;
13 const int maxn = 5100;
14 const int mod = 100000007;
15 ll n, k, m, pre, r;
16 int isprime(int x)
17 {
18     if (x == 1)
19         return 0;
20     if (x == 2)
21         return 0;
22     int m = sqrt(x) + 1;
23     for (int i = 2; i <= m; i++)
24         if (x % i == 0)
25             return 0;
26     return 1;
27 }
28 int main(int argc, char const *argv[])
29 {
30     int tot = 1, t;
31     while (scanf("%d", &t) && t > 0)
32     {
33         printf("%d: ", tot++);
34         if (isprime(t))
35             puts("yes");
36         else
37             puts("no");
38     }
39     return 0;
40 }

View Code

V - Maximum GCD

Description

输入一行数据，输出其最大公约数

Solution

注意读入

 1 // #include <bits/stdc++.h>
 2 #include <cmath>
 3 #include <cstdio>
 4 #include <cstring>
 5 #include <iostream>
 6 #include <vector>
 7 #define lson rt << 1, l, mid
 8 #define rson rt << 1 | 1, mid + 1, r
 9 using namespace std;
10 // using ll = long long;
11 // using ull = unsigned long long;
12 // using pa = pair<int, int>;
13 // using ld = long double;
14 typedef long long ll;
15 const int maxn = 5100;
16 const int mod = 100000007;
17 char s[maxn];
18 int gcd(int a, int b)
19 {
20     return b ? gcd(b, a % b) : a;
21 }
22 int main(int argc, char const *argv[])
23 {
24     // ios::sync_with_stdio(false);
25     // cin.tie(0);
26     // cout.tie(0);
27     int t;
28     cin >> t;
29     getchar();
30     while (t--)
31     {
32         int ans = 0;
33         gets(s);
34         int cur = 0;
35         int sz = strlen(s);
36         vector<int> aa;
37         aa.clear();
38         for (int i = 0; i < sz; i++)
39         {
40             int sum = 0;
41             while (i < sz && s[i] != ' ')
42             {
43                 sum = sum * 10 + s[i] - '0';
44                 i++;
45             }
46             aa.push_back(sum);
47         }
48 
49         sz = aa.size();
50         for (int i = 0; i < sz - 1; i++)
51             for (int j = i + 1; j < sz; j++)
52                 ans = max(ans, gcd(aa[i], aa[j]));
53         cout << ans << "
";
54     }
55     return 0;
56 }

View Code

W - Prime Time

Description

输入两个区间端点，判断区间内有多少素数，给出百分比

Solution

数据较小，暴力即可

卡精度，需要加eps

 1 /*
 2     卡精度真的恶心，记得最后加一个eps
 3  */
 4 #pragma optimize(3)
 5 #include <bits/stdc++.h>
 6 #define lson rt << 1, l, mid
 7 #define rson rt << 1 | 1, mid + 1, r
 8 using namespace std;
 9 using ll = long long;
10 using ull = unsigned long long;
11 using pa = pair<int, int>;
12 using ld = long double;
13 int n, m, k, mod;
14 const int maxn = 1e8 + 1e5;
15 template <class T>
16 inline T read(T &ret)
17 {
18     int f = 1;
19     ret = 0;
20     char ch = getchar();
21     while (!isdigit(ch))
22     {
23         if (ch == '-')
24             f = -1;
25         ch = getchar();
26     }
27     while (isdigit(ch))
28     {
29         ret = (ret << 1) + (ret << 3) + ch - '0';
30         ch = getchar();
31     }
32     ret *= f;
33     return ret;
34 }
35 template <class T>
36 inline void write(T n)
37 {
38     if (n < 0)
39     {
40         putchar('-');
41         n = -n;
42     }
43     if (n >= 10)
44     {
45         write(n / 10);
46     }
47     putchar(n % 10 + '0');
48 }
49 bool vis[maxn];
50 int prime[maxn / 10], pcnt;
51 void init()
52 {
53     for (int i = 2; i <= maxn; i++)
54     {
55         if (!vis[i])
56             prime[pcnt++] = i;
57         for (int j = 0; j < pcnt && i * prime[j] <= maxn; j++)
58         {
59             vis[i * prime[j]] = 1;
60             if (i % prime[j] == 0)
61                 break;
62         }
63     }
64 }
65 inline int isprime(int x)
66 {
67     return !vis[x];
68 }
69 inline int f(int x)
70 {
71     return x * x + x + 41;
72 }
73 int main(int argc, char const *argv[])
74 {
75     ios::sync_with_stdio(false);
76     cin.tie(0);
77     cout.tie(0);
78     int a, b;
79     init();
80     while (cin >> a >> b)
81     {
82         ld mu = b - a + 1;
83         ld deno = 0;
84         for (int i = a; i <= b; i++)
85             deno += isprime(f(i));
86         ld ans = deno / mu * 100;
87         cout << fixed << setprecision(2) << ans + 1e-5 << "
";
88     }
89     return 0;
90 }

View Code

X - Farey Sequence

Description

欧拉函数前缀和

Solution

 1 #pragma optimize(3)
 2 // #include <bits/stdc++.h>
 3 #include <cstdio>
 4 #include <cstring>
 5 #include <iostream>
 6 #define lson rt << 1, l, mid
 7 #define rson rt << 1 | 1, mid + 1, r
 8 using namespace std;
 9 // using ll = long long;
10 // using ull = unsigned long long;
11 // using pa = pair<int, int>;
12 // using ld = long double;
13 typedef long long ll;
14 int n, m, k, mod;
15 const int maxn = 1e6 + 100;
16 ll f[maxn];
17 int phi[maxn], vis[maxn], prime[maxn], cnt;
18 void init()
19 {
20     phi[1] = 1;
21     int cnt = 0;
22     for (int i = 2; i < maxn; i++)
23     {
24         if (!vis[i])
25         {
26             prime[cnt++] = i;
27             phi[i] = i - 1;
28         }
29         for (int j = 0; j < cnt && i * prime[j] < maxn; j++)
30         {
31             vis[i * prime[j]] = true;
32             if (i % prime[j] == 0)
33             {
34                 phi[i * prime[j]] = phi[i] * prime[j];
35                 break;
36             }
37             else
38             {
39                 phi[i * prime[j]] = phi[i] * phi[prime[j]]; // phi[i]*(prime[j]-1);
40             }
41         }
42     }
43     f[2] = 1;
44     for (int i = 3; i < maxn; i++)
45         f[i] = f[i - 1] + phi[i];
46 }
47 int main(int argc, char const *argv[])
48 {
49     ios::sync_with_stdio(false);
50     cin.tie(0);
51     cout.tie(0);
52     int a, b;
53     init();
54     while (cin >> a && a)
55     {
56         cout << f[a] << "
";
57     }
58     return 0;
59 }

View Code

Y - The Super Powers

Description

求2^64-1内至少能表示出两个幂的数，打印出来

Solution

暴力打表，注意边界

 1 /*
 2     暴力打表
 3  */
 4 #pragma optimize(3)
 5 // #include <bits/stdc++.h>
 6 #include <cmath>
 7 #include <cstdio>
 8 #include <cstring>
 9 #include <iostream>
10 #include <set>
11 #define lson rt << 1, l, mid
12 #define rson rt << 1 | 1, mid + 1, r
13 using namespace std;
14 // using ll = long long;
15 // using ull = unsigned long long;
16 // using pa = pair<int, int>;
17 // using ld = long double;
18 typedef long long ll;
19 typedef unsigned long long ull;
20 int n, m, k, mod;
21 const int maxn = 1e6 + 100;
22 ll f[maxn];
23 int phi[maxn], vis[maxn], prime[maxn], cnt;
24 unsigned long long maxx = (1ULL << 64ULL) - 1;
25 set<ull> s;
26 ull qpow(ull a, int b)
27 {
28     ull res = 1;
29     while (b)
30     {
31         if (b & 1)
32             res *= a;
33         a *= a;
34         b >>= 1;
35     }
36     return res;
37 }
38 void init()
39 {
40     phi[1] = 1;
41     int cnt = 0;
42     for (int i = 2; i < maxn; i++)
43     {
44         if (!vis[i])
45         {
46             prime[cnt++] = i;
47             phi[i] = i - 1;
48         }
49         for (int j = 0; j < cnt && i * prime[j] < maxn; j++)
50         {
51             vis[i * prime[j]] = true;
52             if (i % prime[j] == 0)
53             {
54                 phi[i * prime[j]] = phi[i] * prime[j];
55                 break;
56             }
57             else
58             {
59                 phi[i * prime[j]] = phi[i] * phi[prime[j]]; // phi[i]*(prime[j]-1);
60             }
61         }
62     }
63 
64     s.insert(1);
65     for (ull i = 2; i < (1 << 16); i++)
66     {
67         ull tmp = i * i * i;
68         int j = 4;
69         while (1)
70         {
71             tmp *= i;
72             if (vis[j])
73                 s.insert(tmp);
74             ++j;
75             if (tmp > maxx / i)
76                 break;
77         }
78     }
79 }
80 int main(int argc, char const *argv[])
81 {
82     ios::sync_with_stdio(false);
83     cin.tie(0);
84     cout.tie(0);
85     int a, b;
86     // freopen("out.txt", "w", stdout);
87     init();
88     for (auto x : s)
89         cout << x << "
";
90     return 0;
91 }

View Code

撒花，数论好难呀

查看全文

相关阅读:
LeetCode第242题：有效的字母异位词
 commons lang组件介绍和学习
 java中如何将string 转化成long
java 字符串按小数点分割
 界面优化处理技术之（一）按钮组件优化处理
 系统登陆界面开发及实现之（五）界面版权组件设置
 系统登陆界面开发及实现之（四）界面登录框组件设置
 系统登陆界面开发及实现之（三）界面标题组件设置
 系统登陆界面开发及实现之（二）添加界面背景图片
 转发：base64引起的血案

原文地址：https://www.cnblogs.com/mooleetzi/p/11321236.html