扩展欧几里德算法:
谁是欧几里德?自己百度去
先介绍什么叫做欧几里德算法
有两个数 a b,现在,我们要求 a b 的最大公约数,怎么求?枚举他们的因子?不现实,当 a b 很大的时候,枚举显得那么的naïve ,那怎么做?
欧几里德有个十分又用的定理: gcd(a, b) = gcd(b , a%b) ,这样,我们就可以在几乎是 log 的时间复杂度里求解出来 a 和 b 的最大公约数了,这就是欧几里德算法,用 C++ 语言描述如下:
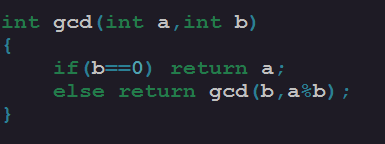
由于是用递归写的,所以看起来很简洁,也很好记忆。那么什么是扩展欧几里德呢?
现在我们知道了 a 和 b 的最大公约数是 gcd ,那么,我们一定能够找到这样的 x 和 y ,使得: a*x + b*y = gcd 这是一个不定方程(其实是一种丢番图方程),有多解是一定的,但是只要我们找到一组特殊的解 x0 和 y0 那么,我们就可以用 x0 和 y0 表示出整个不定方程的通解:
x = x0 + (b/gcd)*t
y = y0 – (a/gcd)*t
为什么不是:
x = x0 + b*t
y = y0 – a*t
这个问题也是在今天早上想通的,想通之后忍不住喷了自己一句弱逼。那是因为:
b/gcd 是 b 的因子, a/gcd 是 a 的因子是吧?那么,由于 t的取值范围是整数,你说 (b/gcd)*t 取到的值多还是 b*t 取到的值多?同理,(a/gcd)*t 取到的值多还是 a*gcd 取到的值多?那肯定又要问了,那为什么不是更小的数,非得是 b/gcd 和a/gcd ?
注意到:我们令 B = b/gcd , A = a、gcd , 那么,A 和 B 一定是互素的吧?这不就证明了 最小的系数就是 A 和 B 了吗?要是实在还有什么不明白的,看看《基础数论》(哈尔滨工业大学出版社),这本书把关于不定方程的通解讲的很清楚
现在,我们知道了一定存在 x 和 y 使得 : a*x + b*y = gcd , 那么,怎么求出这个特解 x 和 y 呢?只需要在欧几里德算法的基础上加点改动就行了。
我们观察到:欧几里德算法停止的状态是: a= gcd , b = 0 ,那么,这是否能给我们求解 x y 提供一种思路呢?因为,这时候,只要 a = gcd 的系数是 1 ,那么只要 b 的系数是 0 或者其他值(无所谓是多少,反正任何数乘以 0 都等于 0 但是a 的系数一定要是 1),这时,我们就会有: a*1 + b*0 = gcd
当然这是最终状态,但是我们是否可以从最终状态反推到最初的状态呢?
假设当前我们要处理的是求出 a 和 b的最大公约数,并求出 x 和 y 使得 a*x + b*y= gcd ,而我们已经求出了下一个状态:b 和 a%b 的最大公约数,并且求出了一组x1 和y1 使得: b*x1 + (a%b)*y1 = gcd , 那么这两个相邻的状态之间是否存在一种关系呢?
我们知道: a%b = a - (a/b)*b(这里的 “/” 指的是整除,例如 5/2=2 , 1/3=0),那么,我们可以进一步得到:
gcd = b*x1 + (a-(a/b)*b)*y1
= b*x1 + a*y1 – (a/b)*b*y1
= a*y1 + b*(x1 – a/b*y1)
对比之前我们的状态:求一组 x 和 y 使得:a*x + b*y = gcd ,是否发现了什么?这里:
x = y1
y = x1 – a/b*y1
以上就是扩展欧几里德算法的全部过程,依然用递归写:

1 #include <iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<deque> 5 #include<stack> 6 #include<algorithm> 7 typedef long long ll; 8 using namespace std; 9 void exgcd(ll a,ll b,ll &x,ll &y) 10 { 11 if(b==0) 12 { 13 x=1; 14 y=0; 15 return ; 16 } 17 exgcd(b,a%b,x,y); 18 ll t=x; 19 x=y; 20 y=t-(a/b)*y; 21 } 22 int main() 23 { 24 ll m,n,x,y,ans; 25 scanf("%lld%lld",&m,&n); 26 exgcd(m,n,x,y); 27 while(x<0) 28 { 29 x+=n; 30 } 31 printf("%lld ",x); 32 return 0; 33 }
