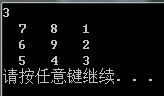
一、输出N*N列蛇形数,如

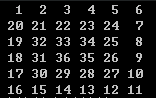
难点在于蛇形圈数,如下
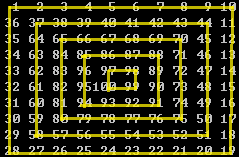
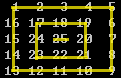
N为10时,圈数为5;N为5时,圈数为3
再推可得出结论:圈数K=(N+1)/2
当N=10时,(int)K=(10+1)/2=5;
当N=5时,(int)K=(5+1)/2=3。
代码如下:
1 #include <stdio.h> 2 3 #define N 10 4 5 int main() 6 { 7 int a[N][N]={0};//初始化全为0 8 int data=1; 9 for(int i =0, j =0, k =0; k <(N+1)/2; k++)//i为行,j为列,k为圈数 10 { 11 while(j<N-k)//控制圈数, 首先赋值第一圈(k=0)第一行,一共N列,减去圈数,即为列尾+1列 12 { 13 a[i][j]=data;//赋值 14 j++;//往右边移动 15 data++; 16 } 17 j--;//退回,while(1)循环后,j=N-k;因为j从0开始,所以一共有N-k-1列,所以要往回退一列,即j-- 18 i++;//转向,接着对第一圈(k=0)第N-1列赋值 19 20 while(i<N-k)//同上,i最大值为N-k-1 21 { 22 a[i][j]=data; 23 i++; 24 data++; 25 } 26 i--;//退回 27 j--;//转向 28 29 while(j>k-1)//当k=0时,j最小为0;当k=1时,j最小为1;。。。所以j>k-1 30 { 31 a[i][j]=data; 32 j--; 33 data++; 34 } 35 j++;//退回 36 i--;//转向 37 38 while(i>k)//当k=0时,i最小为1;当k=1时,i最小为2;。。。所以i>k 39 { 40 a[i][j]=data; 41 i--; 42 data++; 43 } 44 i++;//退回 45 j++;//转向 46 } 47 48 for(int i =0; i < N;++i) 49 { 50 for(int j =0; j < N;++j) 51 { 52 printf("%3d", a[i][j]); 53 } 54 printf(" "); 55 } 56 57 return 0; 58 }

二、
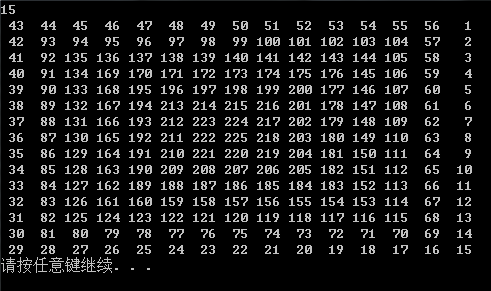
/***************************************************************************************** 蛇形填数 时间限制:3000 ms | 内存限制:65535 KB 难度:3 描述 在n*n方陈里填入1,2,...,n*n,要求填成蛇形。例如n=4时方陈为: 10 11 12 1 9 16 13 2 8 15 14 3 7 6 5 4 输入 直接输入方陈的维数,即n的值。(n<=100) 输出 输出结果是蛇形方陈。 样例输入 3 样例输出 7 8 1 6 9 2 5 4 3 *****************************************************************************************/ #include <stdio.h> #define N 100 int main() { int n,data=1; scanf("%d",&n); int a[N][N]={0}; for(int i=0,j=n-1,k=0; k<(n+1)/2; k++)//K循环层数 { while(i<n-k) { a[i][j]=data; i++; data++; } i--; j--; while(j>k-1) { a[i][j]=data; j--; data++; } j++; i--; while(i>k-1) { a[i][j]=data; i--; data++; } i++; j++; while(j<n-k-1) { a[i][j]=data; j++; data++; } j--; i++; } for(int i =0; i < n;++i) { for(int j =0; j < n;++j) { printf("%3d ", a[i][j]); } printf(" "); } return 0; }