逻辑斯谛回归(Logistic Regression)【又名逻辑回归,对率回归,对数几率回归】:函数、模型及其理论内涵
逻辑斯谛函数(logistic function)【即sigmoid函数】:函数形式的来源
逻辑斯谛函数的形式为:
这个函数形式的产生和来历实际上来自于生态学的理论。生态学的研究涉及到不同尺度,从种群到群落到整个生态系统。其中,对于种群生态学,即主要考虑单一物种的生存模式和状态的研究中,关于种群的个体的数量变化,有所谓的马尔萨斯模型和逻辑斯蒂模型。简要来说,所谓马尔萨斯模型是指种群在某一状态下的增长速率与这一状态下种群的大小成正比,也就是说,种群越大,增速也就越快。这个很容易理解,因为种群越大,可以生殖的个体的数目就越多,自然增速就大,所谓人口的指数型增长也就是来自于这个理论模型。把这个正比关系的模型假设写成微分方程,即可得到:
显然,微分后还是自己(差了一个常数r)的函数,其实就是指数函数,因此这个实质上就是个指数模型。
但是,这个模型有个不足之处,在模型建构上,它只考虑了“生”的过程,没有考虑“存”的实际情况;在模型结果上,它会导致无限制的增长,这显然是与很多观测不符的。生的速率确实和N成正比,但是存活下来与否还要收到环境因素的制约,也就是生态学上讲的环境容纳量(capacity)。这个容纳量是由于种内竞争引起的,即种内生物要争夺有限的资源,所以使得种群大到一定程度以后,增长率会下降,于是有人对上面的模型进行改进,考虑到这个因素。这就是逻辑斯蒂模型:
这里的K就是capacity。对于上面的这个微分方程,左右同乘以K,那么就会发现,一个函数的导数等于该函数乘以1减去该函数,再乘上一个系数。对于这种形式:
的函数f(x),如果学过神经网络的BP算法,并且做过最后一个sigmoid激活层求导的话,就能看出来,满足这个方程的函数就是逻辑斯底函数,也叫sigmoid函数。
ps:扩展阅读:生活史对策,r-选择与K-选择
机器学习中的logistic function:选择该函数的动因
那么为何在机器学习的分类或回归问题中选择逻辑斯蒂函数呢?首先,看该函数的形状:
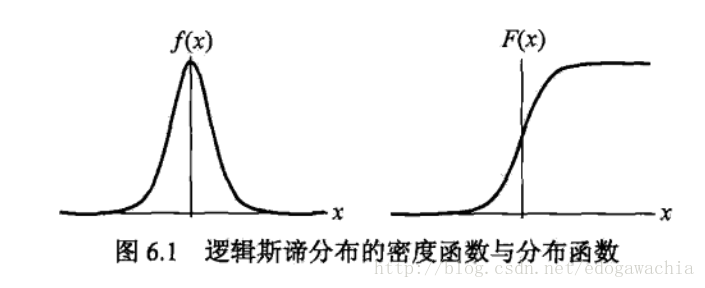
按照上一节的生态学意义来说,左边就是增长率(dN/dt)的变化曲线,右边就是种群规模(N)的变化曲线。对于我们的分类问题,即已知许多特征x,希望通过这些特征预测出label,就是类别的标签,对于二分类问题,标签只有两个,这里记做0和1(有的记做+1和-1)。对于x,我们希望用一个模型,最终综合起所有的特征x,然后得到一个待判决的数值,要想判断具体属于哪一类,需要设定一个阈值,大于这个阈值给一个类别,小于则给另一个类别,就像最基本的高维空间用超平面分割两类一样。这样,我们实际上还需要一个带有阈值的阶跃函数,小于某个值函数值为0,大于为1。
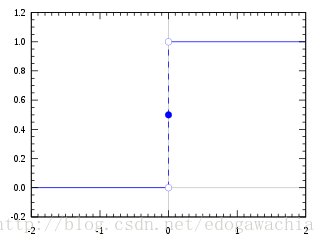
如果这个待判决数值由特征的线性组合产生,那么最终的判别结果就是:
stepfun就是阶跃函数,由于有bias,所以阈值直接给0就可以。因为bias可以选取。但是阶跃函数不可导,由于我们要学习参数w和b势必要求导,因此我们用logistic来代替阶跃,用来作为一个阈值判别器。
logistic有诸多好处,首先,它是光滑可导的,为学习提供了方便;另外,它是有界的,界就是0到1,也就是说,它可以把-inf到+inf的线性函数的输出压缩到0~1,而且在x=0处,函数值为0.5,刚好可以作为阈值;0~1正好也是概率的范围,因此可以用它模拟概率。因此选择它作为机器学习的激活函数,或者说模型函数。
逻辑斯谛回归 :对数几率释名,以及代价函数的生成
这样,逻辑斯谛回归的表达式可以写成:

可以看出,就是用来模拟了在x下y=0或1的概率p。
logistic函数又叫对率函数,即对数几率,首先,几率指的是:
而对数几率就是对odds取对数,通常叫做logit函数 。在看一些神经网络的code的时候经常会遇到叫做logit的变量,就是这个含义。那么,将上面的p取logit,那么:
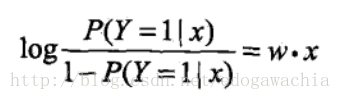
也就是说,用线性函数去拟合了Y=1的对数几率,因此叫做对率函数,对率回归。
那么,怎样去估计模型参数呢?这里考虑极大似然估计法(MLE),这是统计学中参数估计的最常见的手法之一,另外还有MAP,最大后验概率。用MLE首先找到似然函数,即在某个参数的模型假设下,发生了实际的样本中的实际数据分布的概率:
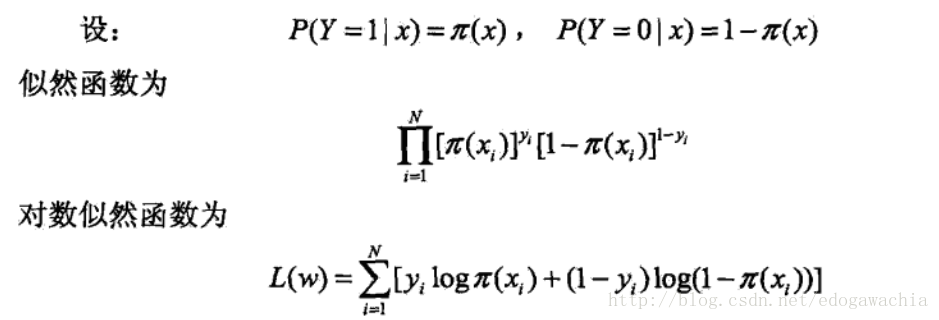
最后得到L(w),加一个负号,就是代价函数。
不同视角下的逻辑斯谛回归:概率论与信息论
从概率意义上来说,优化cost function实际上就是在做MLE,也就是说,我们认为,能够大概率使得我们现有的样本数据发生的模型参数才是最靠谱的。实际上,logistic虽然处理分类问题,但是它是先产生了概率p,再进行阈值判断,前面的过程实际上就是一个回归的过程。
从信息熵的角度来看,我们看到L(w)的表达式,这是一个统计意义上的表达式,如果写成概率的形式,可以看成:
我们需要min cost。p0,p1就是给定一个x下,Y被分类为0和分类为1的概率,这个cost就是信息熵。那么可以理解为,我们希望让这个分布的信息量尽可能的小,也就是说,混乱度小,或者说,只要我们知道了x,那么这个x为特征的样本属于某一类这个事件的发生对于我们而言是trivial的,这也就说明我们从x中已经对Y有了足够的推断,因此cost小则说明模型预测能力强。
2018年02月22日23:45:44
reference:李航,统计学习方法 【文中截图来源于此书】
