最大半连通子图（tarjan缩点+拓扑）

题目

半联通子图，即只需要两两点之间单向联通，如果有强联通分量，里面的点都是满足条件的。

所以我们可以先缩点，转换成DAG，再考虑其性质。

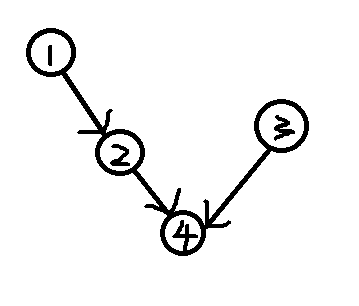
如果缩点之后呈现这种图，那么一定是不合法的。

也就是说，我们只需要在拓扑过程中找到最长链即可。

但直接找会出现问题，题目中还要求求出个数，如果有重边的话，会将同一种连边关系累加多次。

所以在拓扑中应该判重！！

判重具体细节见代码。

#include<bits/stdc++.h>
using namespace std;
#define ri register int
#define N 100005
#define M 1000005
#define ll long long
int n,m,mod,dp[N],low[N],dfn[N],Ti=0,flag[N],stk[N],top=0,tot=0,cnt=0;
int head[N],nex[M],to[M],bel[N],ru[N],cntt[N],chong[N],sum[N];
void add(int a,int b) { to[++tot]=b; nex[tot]=head[a]; head[a]=tot; }
vector<int> scc[N];
vector<int> e[N];
void tarjan(int x)
{
    dfn[x]=low[x]=++Ti;
    stk[++top]=x; flag[x]=1;
    for(ri i=head[x];i;i=nex[i]){
        int v=to[i];
        if(!dfn[v]){ tarjan(v); low[x]=min(low[x],low[v]); }
        else if(flag[v]) low[x]=min(low[x],dfn[v]);
    }
    if(low[x]==dfn[x]){
        cnt++;
        do{
            int tmp=stk[top];
            scc[cnt].push_back(tmp); flag[tmp]=0;
            bel[tmp]=cnt;
        }while(stk[top--]!=x);
    }
}
queue<int> q;
void topu()//size
{
    ll maxn=0,num=0;
    memset(dp,-10,sizeof(dp));
    for(ri i=1;i<=cnt;++i) if(!ru[i]) q.push(i),dp[i]=sum[i],cntt[i]=1;
    while(!q.empty()){
        int u=q.front(); q.pop();
        if(dp[u]>maxn) maxn=dp[u],num=cntt[u];
        else if(dp[u]==maxn) num=(num+cntt[u])%mod;
        for(ri i=0;i<e[u].size();++i){
            int v=e[u][i]; ru[v]--;//如果是重边也要将入度-- 因为之前算入过 
            if(!chong[v]){
                chong[v]=1;
                int xx=sum[v];
                if(dp[u]+xx>dp[v]) dp[v]=dp[u]+xx,cntt[v]=cntt[u];
                else if(dp[u]+xx==dp[v]) cntt[v]=(cntt[v]+cntt[u])%mod;
            } 
            if(ru[v]==0) q.push(v);//即使是重边也要判断在减了之后能否入队 
        }
        for(ri i=0;i<e[u].size();++i) chong[e[u][i]]=0;//判断重边 
    }
    printf("%lld
%lld
",maxn,num);
}
int main()
{
    scanf("%d%d%d",&n,&m,&mod);
    int a,b;
    for(ri i=1;i<=m;++i) scanf("%d%d",&a,&b),add(a,b);
    for(ri i=1;i<=n;++i) if(!dfn[i]) tarjan(i);
    for(ri i=1;i<=n;++i){
        sum[bel[i]]++;
        for(ri j=head[i];j;j=nex[j]){
            int v=to[j];
            if(bel[i]==bel[v]) continue;
            e[bel[i]].push_back(bel[v]); ru[bel[v]]++;
        }
    }
    topu();
}
/*
3 2 1000000007
1 2
1 2
*/