杂言
但凡是有这句话的就是我没写完就发出来了,还差个时间戳优化 ,欢迎催更
在此鸣谢oi-wiki
认识一下
树状数组能办到的 线段树都可以,反之不亦然,,在解决单点问题时,显然用代码量更短树状数组更好 因为懒(雾
原理
大节点记录某些小节点的信息,节省查询次数
下图为 c 数组的示意图,维护 a 数组(初始数列)的信息,不难看出,c[1]维护a[1], c[2]维护a[1]&a[2],c[3]维护a[3],c[4]维护a[1]&a[2]&a[3]&a[4]...., a 数组多大 c 数组开多大就ok
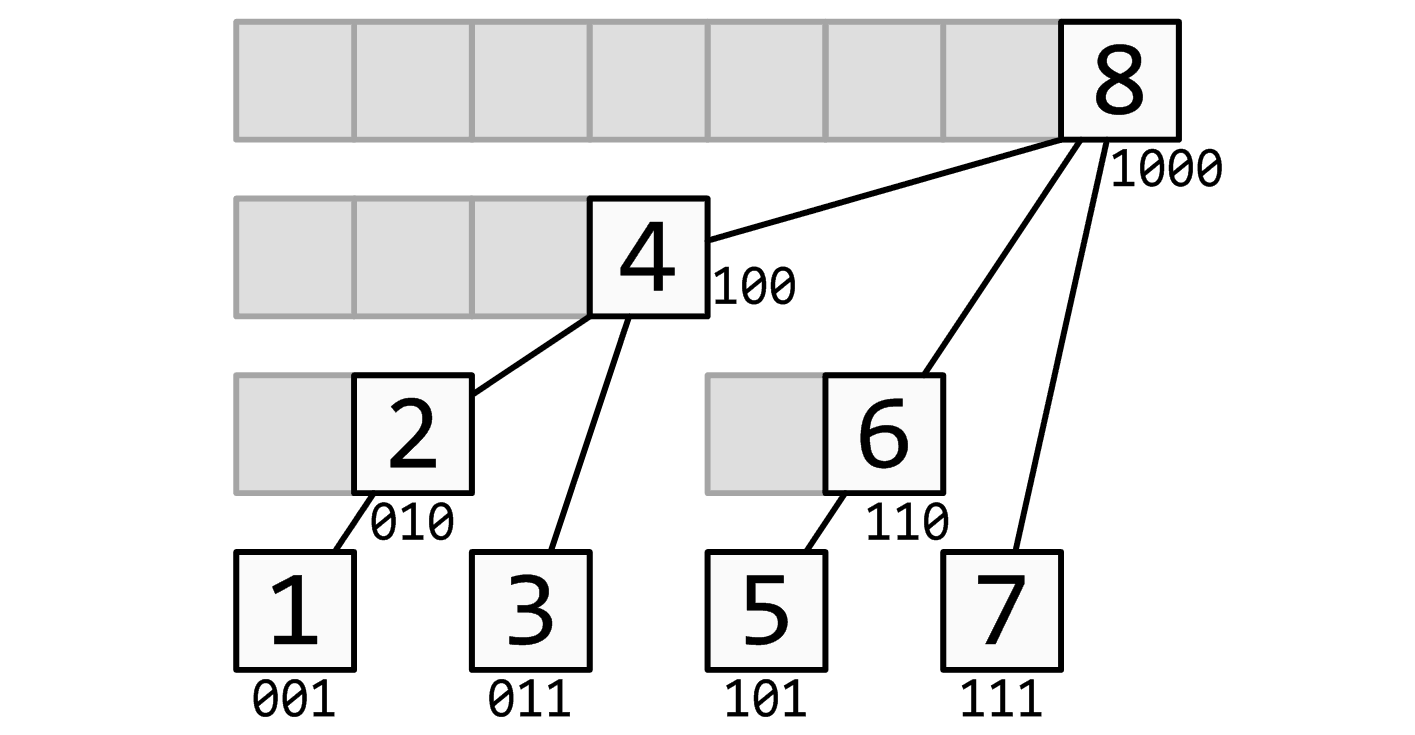
举个栗子,假设要算 a[51]~a[91] 的区间和, (当然这是用小区间举个栗子而已不要用暴力反驳毕竟区间范围大了暴力就RE了),,从91往前跳,用某种操作找到维护 a[91] 的 c[n] (n可用某种操作求出) 发现此 c[n] 只维护 a[91] ,再往前找,该找 a[90] ,发现 c[n-1] 维护的是 a[89]&a[90],就会直接跳到 a[88],接着向前跳..
某种操作
lowbit,一个代码量小到没话说而且很关键的函数,用来计算 c 维护的 a 的个数
int lowbit(int x) { return x & -x; }
算出 x 二进制的最后一个 1 以及这个 1 之后的那些 0 组成的二进制对应的十进制的数
举个栗子,
x = 88(10) = 01011000(2)
-x = -88(10) = (10100111(2) + 1(2)) = 10101000(2)
x & (-x) = 1000(2) = 8(10)
神 奇
单点修改O(logn) ↓
void add(int x, int k) {
while (x <= n) { // 不能越界
c[x] += k;
x = x + lowbit(x);
}
}
每次只在他的上级那里更新就好了 ,,求和 ↓,,求a[51]~a[91]的话用 sum(91) - sum(51-1) , 因为 a[51] 的值也要算进去,,,
求前缀和O(logn) ↓
int sum(int x) { // a[1]……a[x]的和
int ans = 0;
while (x > 0) {
ans += c[x];
x -= lowbit(x);
}
return ans;
}
区间加 & 区间求和
对不起原来是我一开始没用markdown改不了了..qwq

关于差分数组,不了解的我直接丢一个链接(某佬的(COLIN·GAO),直接搬过来了,冒犯)
于是对于区间 [ l , r ] 每个数都 +x , 只令 b[l] += x , b[r+1] -= x , 就可以了 , 显然对于区间 [ l, r ]的和为 sum[r] - sum[l-1] (sum[]是用查分数组 b 来计算 a 的前缀和的值)
设两棵树为 t1, t2,
区间修改 ↓
void add(int k, int v1){ int v2 = k * v1; //维护的是bi*i的 while (k <= n) { t1[k] += v1, t2[k] += v2; k += lowbit(k); } } void addd(int l, int r, int v) { add(l, v); //b[l] += x; add(r + 1, -v); //b[r+1] -= x ; }
区间求和 ↓
int getsum(int *t, int k) { int ret = 0; while (k) { ret += t[k]; k -= lowbit(k); } return ret; } long long getsum1(int l, int r) { return (r + 1ll) * getsum(t1, r) - 1ll * l * getsum(t1, l - 1) -(getsum(t2, r) - getsum(t2, l - 1)); }
manipulate
O(n)建树
每个节点的值 都是 所有与自己直接相连的儿子 的和 得到的 , 所以可以在更新儿子的的值的同时顺手把自己的贡献加到父亲上
void build() {
for (int i=1; i<=n; ++i) {
t[i] += a[i];
int j = i + lowbit(i);
if (j<=n) t[j] += t[i];
}
}
O(log n)查询第 k 小(大)的数
查询第 k 大可以转化为查询 (n-k+1) 小的数 ,


int kth(int k) { int cnt = 0, ret = 0; for (int i=log2(n); ~i; i--) { // i与上文depth含义相同 ret += 1 << i; // 尝试扩展 if (ret >= n || cnt + t[ret] >= k) // 如果扩展失败 ret -= 1 << i; else cnt += t[ret]; // 扩展成功后 要更新之前求和的值 } return ret + 1; }
撒花(。・・)ノ❀❀,,
未完待续..