CenterNet文献调研记录。
本文部分思路参考:
1. Anchor-Free
2. https://zhuanlan.zhihu.com/p/66048276
3. https://blog.csdn.net/u014380165/article/details/92801206
在此由衷感谢。
一些专业词汇概念需要掌握:
一、上下采样的概念: https://blog.csdn.net/stf1065716904/article/details/78450997
1. 缩小图像(或称为下采样(subsampled)或降采样(downsampled))的主要目的有两个:
1、使得图像符合显示区域的大小;
2、生成对应图像的缩略图。
下采样原理:对于一幅图像I尺寸为M*N,对其进行s倍下采样,即得到(M/s)*(N/s)尺寸的得分辨率图像,当然s应该是M和N的公约数才行,如果考虑的是矩阵形式的图像,就是把原始图像s*s窗口内的图像变成一个像素,这个像素点的值就是窗口内所有像素的均值:
2. 放大图像(或称为上采样(upsampling)或图像插值(interpolating))的主要目的是放大原图像,从而可以显示在更高分辨率的显示设备上。对图像的缩放操作并不能带来更多关于该图像的信息, 因此图像的质量将不可避免地受到影响。然而,确实有一些缩放方法能够增加图像的信息,从而使得缩放后的图像质量超过原图质量的。
上采样原理:图像放大几乎都是采用内插值方法,即在原有图像像素的基础上在像素点之间采用合适的插值算法插入新的元素。
无论缩放图像(下采样)还是放大图像(上采样),采样方式有很多种。如最近邻插值,双线性插值,均值插值,中值插值等方法。在AlexNet中就使用了较合适的插值方法。各种插值方法都有各自的优缺点。
二、超参数:所谓超参数,就是机器学习模型里面的框架参数,比如聚类方法里面类的个数,或者话题模型里面话题的个数等等,都称为超参数。它们跟训练过程中学习的参数(权重)是不一样的,通常是手工设定,不断试错调整,或者对一系列穷举出来的参数组合一通枚举(叫做网格搜索)。
三、loss函数的意义 https://zhuanlan.zhihu.com/p/49981234
机器学习中的监督学习本质上是给定一系列训练样本,尝试学习
的映射关系,使得给定一个
,即便这个
不在训练样本中,也能够输出
,尽量与真实的
接近。损失函数是用来估量模型的输出
与真实值
之间的差距,给模型的优化指引方向。
四、focal loss的概念 摘自 :https://www.cnblogs.com/areaChun/p/11900799.html
我们知道object detection的算法主要可以分为两大类:two-stage detector和one-stage detector。前者是指类似Faster RCNN,RFCN这样需要region proposal的检测算法,这类算法可以达到很高的准确率,但是速度较慢。虽然可以通过减少proposal的数量或降低输入图像的分辨率等方式达到提速,但是速度并没有质的提升。后者是指类似YOLO,SSD这样不需要region proposal,直接回归的检测算法,这类算法速度很快,但是准确率不如前者。作者提出focal loss的出发点也是希望one-stage detector可以达到two-stage detector的准确率,同时不影响原有的速度。
作者认为one-stage detector的准确率不如two-stage detector的原因是:样本不均衡问题,其中包括两个方面:
- 解决样本的类别不平衡问题
- 解决简单/困难样本不平衡问题
为了解决(1)解决样本的类别不平衡问题和(2)解决简单/困难样本不平衡问题,作者提出一种新的损失函数:focal loss。这个损失函数是在标准交叉熵损失基础上改进得到:
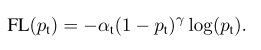
该focal loss函数曲线为: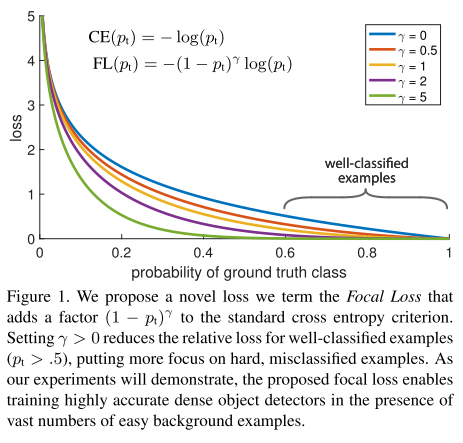
其中,−log(pt)为初始交叉熵损失函数,α 为类别间(0-1二分类)的权重参数,(1−pt)γ 为简单/困难样本调节因子(modulating factor),而γ 则聚焦参数(focusing parameter)。
1、形成过程:
(1)初始二分类的交叉熵(Cross Emtropy, CE)函数:
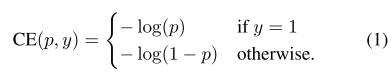
在上面的y∈{±1}y∈{±1} 为指定的ground-truth类别,p∈[0,1]p∈[0,1] 是模型对带有 y=1y=1 标签类别的概率估计。为了方便,我们将ptpt定义为:
和重写的CE(p,y)CE(p,y):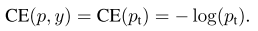
(2)平衡交叉熵(Balanced Cross Entropy):
一个普遍解决类别不平衡的方法是增加权重参数α∈[0,1]α∈[0,1],当$ y=1 类的权重为类的权重为alpha$ ,y=−1y=−1 类的权重为1−α1−α 。在实验中,αα 被设成逆类别频率(inverse class frequence),αtαt定义与ptpt一样: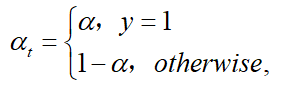
因此,α−balancedα−balanced 的CE损失函数为: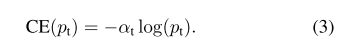
(3)聚焦损失(Focal Loss):
尽管α能平衡positive/negative的重要性,但是无法区分简单easy/困难hard样本。为此,对于简单的样本增加一个小的权重(down-weighted),让损失函数聚焦在困难样本的训练。
因此,在交叉熵损失函数增加调节因子(1−pt)γ(1−pt)γ ,和可调节聚参数γ≥0γ≥0。,所以损失函数变成: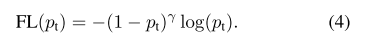
当pt→0时,同时调节因子也 (1−pt)γ→0 ,因此简单样本的权重越小。直观地讲,调节因子减少了简单示例的loss贡献,并扩展了样本接收低loss的范围。 例如,在γ= 2的情况下,与CE相比,分类为pt = 0.9的示例的损失将降低100倍,而对于pt≈0.968的示例,其损失将降低1000倍。 这反过来增加了纠正错误分类示例的重要性(对于pt≤0.5和γ= 2,其损失最多缩小4倍)。
(4)最终的损失函数Focal Loss形式:
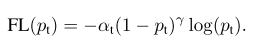
根据论文作者实验,α=0.25 和 γ=2 效果最好
实现代码:
def focal_loss(y_true, y_pred): alpha, gamma = 0.25, 2 y_pred = K.clip(y_pred, 1e-8, 1 - 1e-8) return - alpha * y_true * K.log(y_pred) * (1 - y_pred)**gamma - (1 - alpha) * (1 - y_true) * K.log(1 - y_pred) * y_pred**gamma
五、L1 - loss(平均绝对损失) https://blog.csdn.net/u013841196/article/details/89923254
平均绝对误差(MAE)是另一种用于回归模型的损失函数。MAE是目标变量和预测变量之间绝对差值之和。因此它衡量的是一组预测值中的平均误差大小,而不考虑它们的方向(如果我们考虑方向的话,那就是均值误差(MBE)了,即误差之和)。范围为0到∞。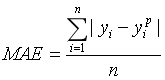

六、什么是高斯核? https://blog.csdn.net/v_july_v/article/details/7624837
特征空间的隐式映射 -- 核函数
核函数的主要目的是将数据映射到高维空间,来解决在原始空间中线性不可分的问题。
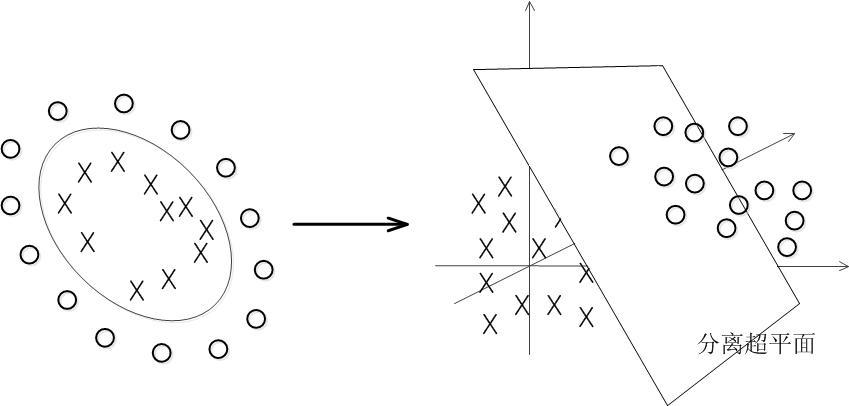
具体来说,在线性不可分的情况下,支持向量机(SVM)首先在低维空间中完成计算,然后通过核函数将输入空间映射到高维特征空间,最终在高维特征空间中构造出最优分离超平面,从而把平面上本身不好分的非线性数据分开。如图所示,一堆数据在二维空间无法划分,从而映射到三维空间里划分,如下图所示。
关于核函数的简要概括:
1. 实际中,我们会经常遇到线性不可分的样例,此时,我们的常用做法是把样例特征映射到高维空间中去(如上文2.2节(具体到给出的链接里有详细的过程)最开始的那幅图所示,映射到高维空间后,相关特征便被分开了,也就达到了分类的目的);
2. 但进一步,如果凡是遇到线性不可分的样例,一律映射到高维空间,那么这个维度大小是会高到可怕的(如上文中19维乃至无穷维的例子)。那咋办呢?
3. 此时,核函数就隆重登场了,核函数的价值在于它虽然也是将特征进行从低维到高维的转换,但核函数绝就绝在它事先在低维上进行计算,而将实质上的分类效果表现在了高维上,也就如上文所说的避免了直接在高维空间中的复杂计算。
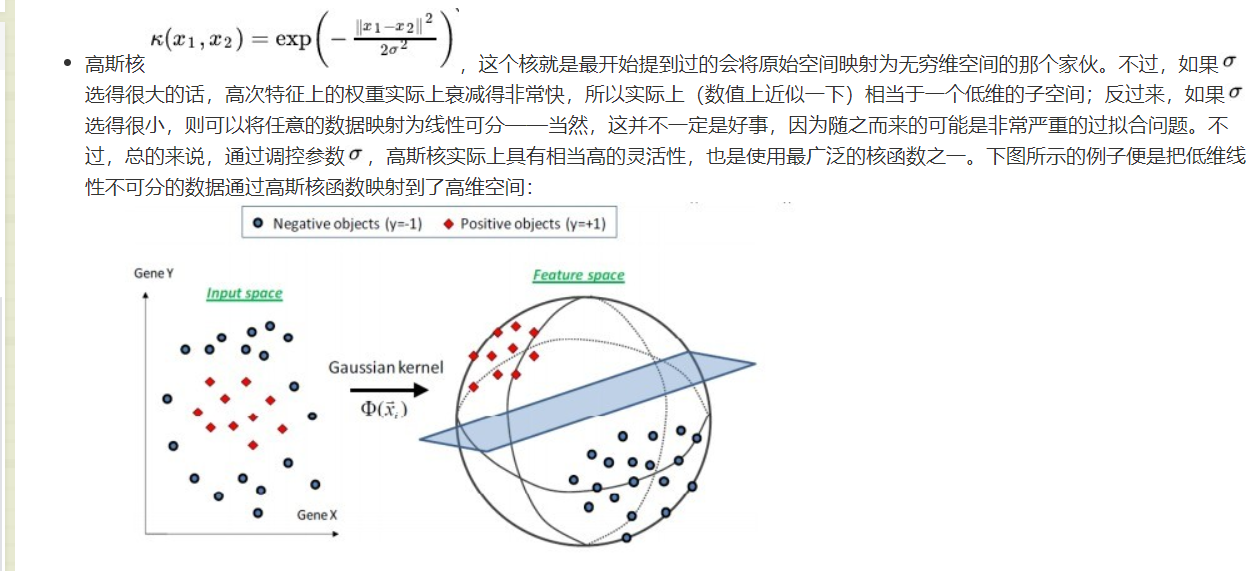
关于高斯核的概念:
六、热度图(Heatmap)的概念 https://www.cnblogs.com/h2zZhou/p/7478497.html
热图可以简单地聚合大量数据,并使用一种渐进的色带来优雅地表现,最终效果一般优于离散点的直接显示,可以很直观地展现空间数据的疏密程度或频率高低。但也由于很直观,热图在数据表现的准确性并不能保证。
生成原理
热图已经不是什么新鲜的概念了,很多领域都在使用。例如记录用户在Web页面内鼠标的点击位置,各种空间离散点数据的显示等等。
其生成的原理简单概括为四个步骤:
(1)为离散点设定一个半径,创建一个缓冲区;
(2)对每个离散点的缓冲区,使用渐进的灰度带(完整的灰度带是0~255)从内而外,由浅至深地填充;
(3)由于灰度值可以叠加(值越大颜色越亮,在灰度带中则显得越白。在实际中,可以选择ARGB模型中任一通道作为叠加灰度值),从而对于有缓冲区交叉的区域,可以叠加灰度值,因而缓冲区交叉的越多,灰度值越大,这块区域也就越“热”;
(4)以叠加后的灰度值为索引,从一条有256种颜色的色带中(例如彩虹色)映射颜色,并对图像重新着色,从而实现热点图。
可以通过几张图来展现这个过程:
(1)灰度带和彩虹色带


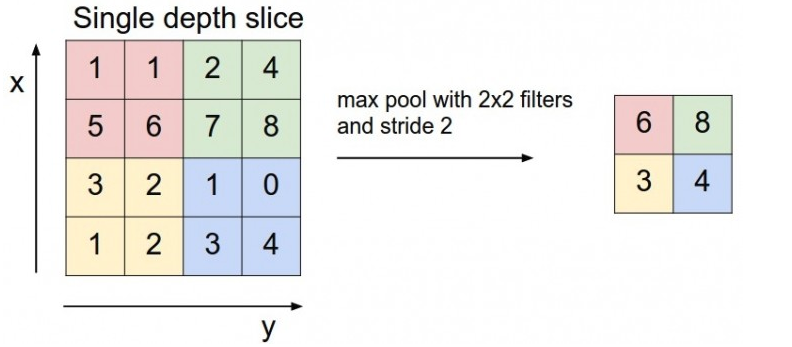
七、Maxpool的概念
(1)偶形式 -- 2X2中最大值
奇形式:
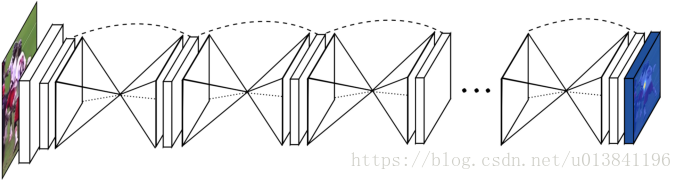
一些前期工作的神经网络模型:
1. Hourglass -- backbone
https://blog.csdn.net/weixin_43292354/article/details/89387651
https://zhuanlan.zhihu.com/p/65123312
1. CornerNet https://blog.csdn.net/StreamRock/article/details/100115681
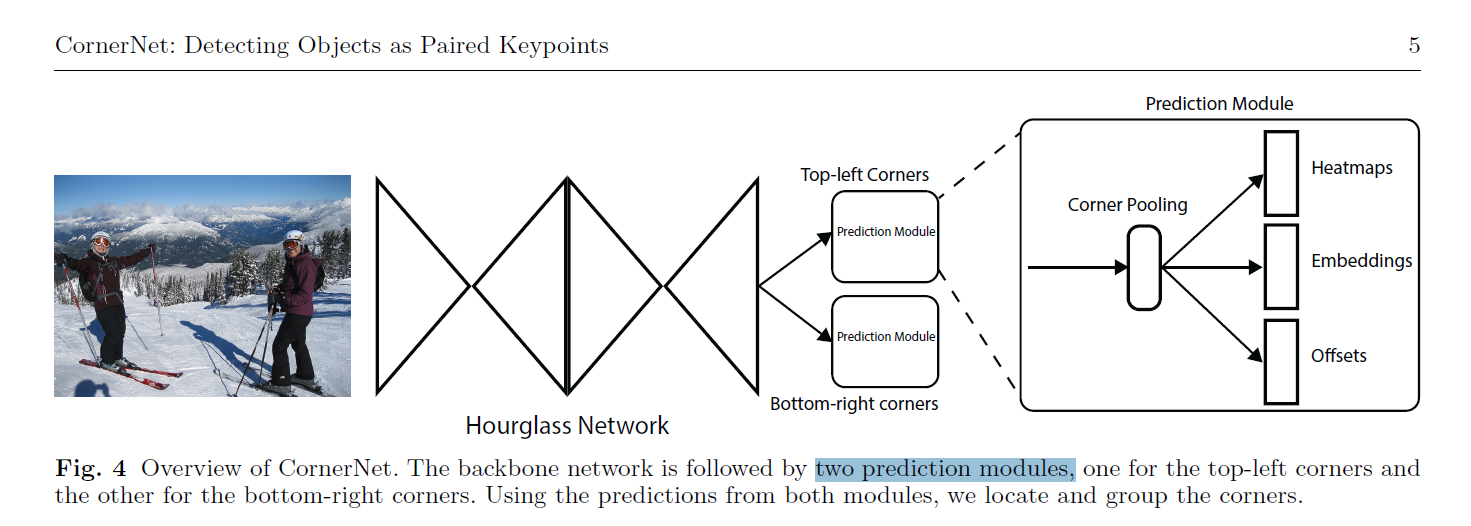
CornerNet和ExtremeNet的区别:
1.CornerNet通过预测角点来检测目标的,而ExtremeNet通过预测极值点和中心点来检测目标的。
2.CornerNet通过角点embedding之间的距离来判断是否为同一组关键点,而ExtremeNet通过暴力枚举极值点、经过中心点判断4个极值点是否为一组。
主要总结内容:
其中心思想:主要用高斯分布来表示目标,就是一个目标用高斯分布来覆盖,目标中心点的值越大。 https://blog.csdn.net/u011622208/article/details/103072220

其网络的主要结构是通过一个backbone生成网络生成Feature map,再通过带分支的检测头分别预测物体的中心点,物体的宽高和heatmap
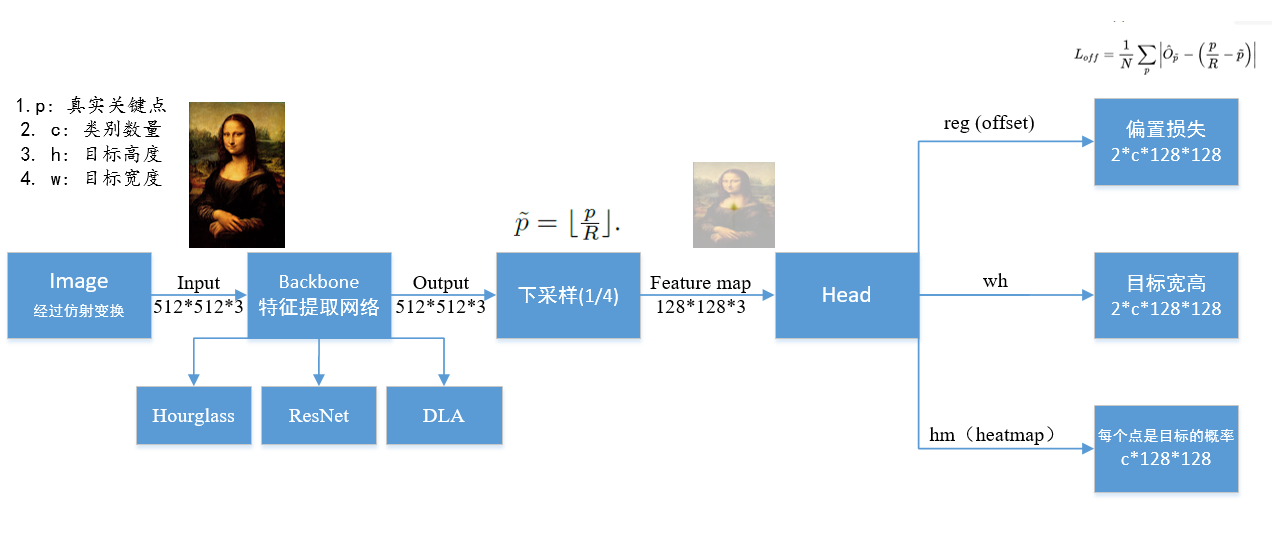
其主要流程为:
1. 输入图像(在这里设图像为h*w*3,也就是长h个像素,宽w个像素,3个通道)
2. 经过仿射变换,这一步重点在于将图像尺寸处理成512*512大小后作为特征提取网络的输入。
3. 经过特征提取网络(作者尝试了三种特征提取网络,分别为Hourglass, ResNet和DLA)进行前向计算,并得到三个输出:
(1)hm (hearmap)大小为[1,80,128,128]. (设类别为80).
(2)wh (目标的长和宽) 大小为[1, 2, 128, 128].
(3)reg (offset,偏置损失),大小为[1, 2, 128, 128].
4.heatmap得到的结果经过sigmiod函数使数值范围规定到[0, 1]之间
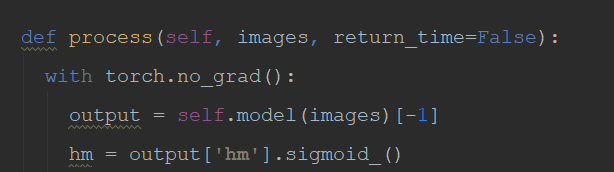
5. 对heatmap执行一个最大池化操作,kernel设置为3,stride设置为1,pad设置为1,这一步其实是在做重复框过滤,这也是为什么后续不再需要NMS操作的一个重要原因,毕竟这里3*3大小的kernel加上特征图和输入图像之间的stride=4,相当于输入图像中每12*12大小的区域都不会有重复的中心点,想法非常简单有效!
6.基于heatmap选择top K个得分最高的点(默认K=100),这样就确定了100个置信度最高的预测框的中心点位置了,这一步也会去掉一定的重复框。接下来就要确定预测框的大小了,通过输出的尺寸预测值和offset就可以得到目前位置
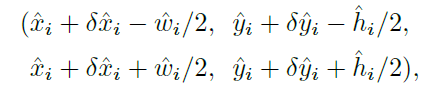
得到的预测框信息都是在128*128大小的特征图上,因此最后将预测框信息再映射到输入图像上就得到最终的预测结果了,
其大致效果如下图所示:
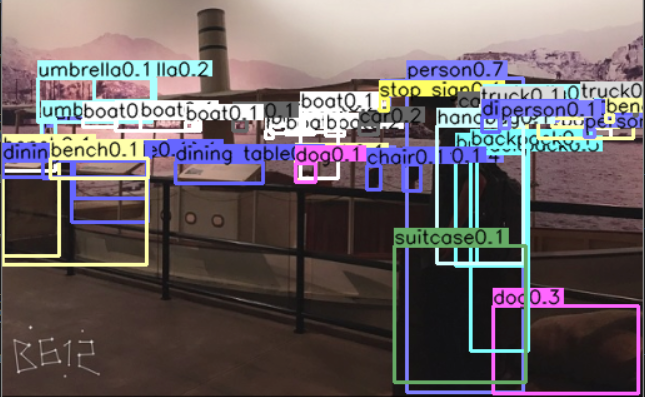
而显示预测结果时作者设定一个置信度阈值,高于阈值的才显示。

所以得到最终结果为:
