公号:码农充电站pro
主页:https://codeshellme.github.io
一般在机器学习的模型训练之前,有一个比较重要的步骤是数据变换。
因为,一般情况下,原始数据的各个特征的值并不在一个统一的范围内,这样数据之间就没有可比性。
数据变换的目的是将不同渠道,不同量级的数据转化到统一的范围之内,方便后续的分析处理。
数据变换的方法有很多,比如数据平滑,数据聚集,数据概化,数据规范化和属性构造等。
本篇文章主要介绍数据规范化,这是一种比较常用,也比较简单的方法。
数据规范化是使属性数据按比例缩放,这样就将原来的数值映射到一个新的特定区域中,包括归一化,标准化等。
1,数据归一化
归一化就是获取原始数据的最大值和最小值,然后把原始值线性变换到 [0,1] 范围之内,变换公式为:
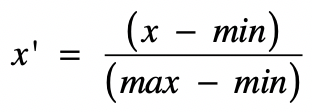
其中:
x是当前要变换的原始值。min是当前特征中的最小值。max是当前特征中的最大值。x'是变换完之后的新值。
注意:
min和max是指当前特征中的最小最大值。
所以同一特征之内,最小最大值是一样的。
而不同特征之间,最小最大值是不一样的。
从公式中可以看出,归一化与最大最小值有关,这也是归一化的缺点,因为最大值与最小值非常容易受噪音数据的影响。
1.1,归一化处理
比如,我们有以下数据:
| 编号 | 特征1 | 特征2 | 特征3 |
|---|---|---|---|
| 第1条 | 5 | 465 | 135 |
| 第2条 | 23 | 378 | 69 |
| 第3条 | 69 | 796 | 83 |
通过数据可以观察出:
Max(特征1) = 69,Min(特征1) = 5Max(特征2) = 796,Min(特征2) = 378Max(特征3) = 135,Min(特征3) = 69
这里我们用第一条数据来举例,看看是如何变换的。
- 对于第一个数字
5做变换:(5 - 5) / (69 - 5) = 0 - 对于第二个数字
465做变换:(465 - 378) / (796 - 378) = 0.21 - 对于第三个数字
135做变换:(135 - 69) / (135 - 69) = 1
1.2,使用 MinMaxScaler 类
sklearn 库的 preprocessing 模块中的 MinMaxScaler 类就是用来做归一化处理的。
首先引入 MinMaxScaler 类:
>>> from sklearn.preprocessing import MinMaxScaler
准备要变换的 data 数据,并初始化 MinMaxScaler 对象:
>>> data = [[5, 465, 135], [23, 378, 69], [69, 796, 83]]
>>> scaler = MinMaxScaler() # 默认将数据拟合到 [0, 1] 范围内
拟合数据:
>>> scaler.fit(data)
输出每个特征的最大最小值:
>>> scaler.data_max_ # 特征最大值
array([ 69., 796., 135.])
>>> scaler.data_min_ # 特征最小值
array([ 5., 378., 69.])
变换所有数据:
>>> scaler.transform(data)
array([[0. , 0.20813397, 1. ],
[0.28125 , 0. , 0. ],
[1. , 1. , 0.21212121]])
可以对比我们计算的第一行数据,结果是一样的。
可以用一个
fit_transform方法,来替换两个方法fit和transform。
2,数据标准化
z-score 标准化是基于正态分布的,该方法假设数据呈现标准正态分布。
2.1,什么是正态分布
正态分布也叫高斯分布,是连续随机变量概率分布的一种,它的数学公式是:
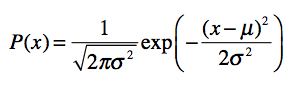
其中,u 为均值(平均数),σ 为标准差。均值和标准差是正态分布的关键参数,它们会决定分布的具体形态。
正态分布有以下特点:
- 正态分布以经过均值 u 的垂线为轴,左右对称展开,中间点最高,然后逐渐向两侧下降。
- 分布曲线和 X 轴组成的面积为 1,表示所有事件出现的概率总和为 1。
正态分布就是常态分布,正常状态的分布。在现实生活中,大量随机现象的数据分布都近似于正态分布。
正态分布的分布图为:
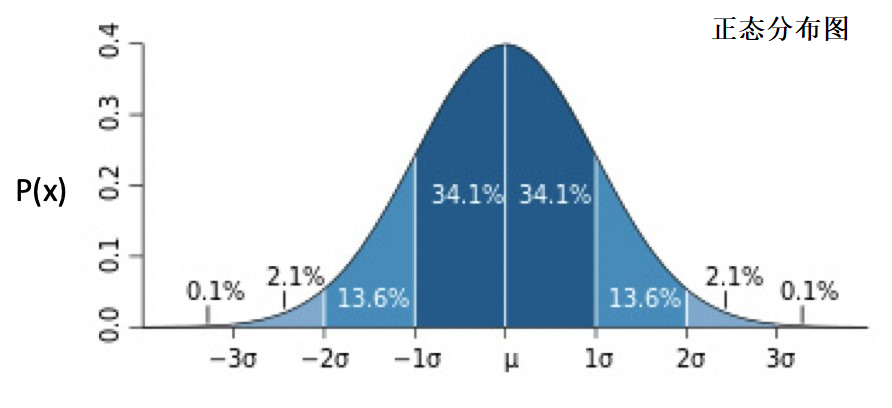
当 μ 为 0,σ 为 1时,正态分布为标准正态分布。
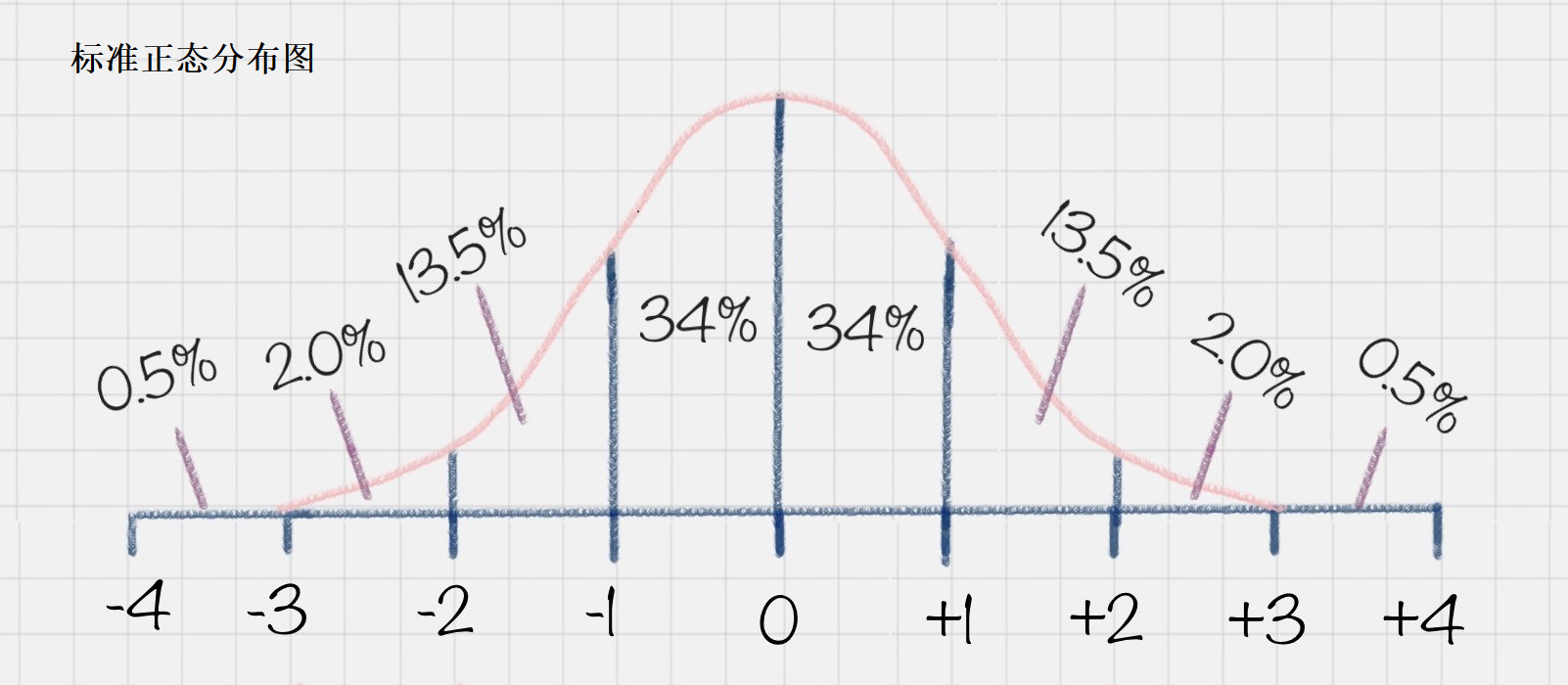
图中的百分数表示所在面积占总面积的百分比。
2.2,z-score 标准化
z-score 标准化利用正态分布的特点,计算一个给定分数距离平均数有多少个标准差。它的转换公式如下:
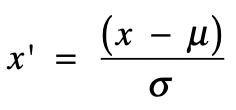
其中 x 为原始值,u 为均值,σ 为标准差,x’ 是变换后的值。
经过 z-score 标准化后,高于平均数的分数会得到一个正的标准分,而低于平均数的分数会得到一个负的标准分数。
和归一化相比,z-score 标准化不容易受到噪音数据的影响,并且保留了各维特征对目标函数的影响权重。
2.3,使用 StandardScaler 类
sklearn 库的 preprocessing 模块中的 StandardScaler 类就是用来做z-score 标准化处理的。
首先引入 StandardScaler 类:
>>> from sklearn.preprocessing import StandardScaler
准备要变换的 data 数据,并初始化 StandardScaler 对象:
>>> data = [
[5, 465, 135],
[23, 378, 69],
[69, 796, 83]
]
>>> scaler = StandardScaler()
拟合数据:
>>> scaler.fit(data)
输出每个特征的均值和标准差:
>>> scaler.mean_ # 均值
array([ 32.33333333, 546.33333333, 95.66666667])
>>> scaler.scale_ # 标准差
array([ 26.94851058, 180.078378 , 28.39405259])
变换所有数据:
>>> scaler.transform(data)
array([[-1.01427993, -0.45165519, 1.38526662],
[-0.34633949, -0.93477815, -0.93916381],
[ 1.36061941, 1.38643334, -0.44610281]])
3,总结
数据变换的目的是将不同渠道,不同量级的数据转化到统一的范围之内,方便后续的分析处理。
不同的机器学习算法,对数据有不同的要求,所以要针对不同的算法,对原始数据进行不同的转换。
数据规范化是常用的数据变化方法,包括归一化和标准化等:
- 归一化:使用特征值中的最大最小值,把原始值转换为 0 到 1 之间的值。
- 优点:是简单易行,好理解。
- 缺点:是容易受最大最小值的干扰。
- 介绍了 MinMaxScaler 类的使用。
- 标准化:介绍了 z-score 标准化,原始数据经过转换后,符合标准正态分布。
- 和归一化相比,z-score 标准化不容易受到噪音数据的影响。
- 介绍了 StandardScaler 类的使用。
数据变换不一定能提高模型的准确度,但是会提高数据的可解释性。
需要注意的是,对训练数据进行了数据变换之后,在测试模型准确度或者预测数据之前,也要对数据进行同样的数据变换。
(本节完。)
推荐阅读:
欢迎关注作者公众号,获取更多技术干货。