公号:码农充电站pro
主页:https://codeshellme.github.io
贝叶斯原理是英国数学家托马斯·贝叶斯于18 世纪提出的,当我们不能直接计算一件事情(A)发生的可能性大小的时候,可以间接的计算与这件事情有关的事情(X,Y,Z)发生的可能性大小,从而间接判断事情(A)发生的可能性大小。

在介绍贝叶斯原理之前,先介绍几个与概率相关的概念。
1,概率相关概念
概率用于描述一件事情发生的可能性大小,用数学符号P(x) 表示,x 表示随机变量,P(x) 表示x 的概率。
随机变量根据变量取值是否连续,可分为离散型随机变量和连续型随机变量。
联合概率由多个随机变量共同决定,用P(x, y) 表示,含义为“事件x 与事件y 同时发生的概率”。
条件概率也是由多个随机变量共同决定,用P(x|y) 表示,含义为“在事件y 发生的前提下,事件x 发生的概率。”
边缘概率:从 P(x, y) 推导出 P(x),从而忽略 y 变量。
- 对于离散型随机变量,通过联合概率
P(x, y)在y上求和, 可得到P(x),这里的P(x)就是边缘概率。 - 对于连续型随机变量,通过联合概率
P(x, y)在y上求积分, 可得到P(x),这里的P(x)就是边缘概率。
概率分布:将随机变量所有可能出现的值,及其对应的概率都展现出来,就能得到这个变量的概率分布,概率分布分为两种,分别是离散型和连续型。
常见的离散型数据分布模型有:
- 伯努利分布:表示单个随机变量的分布,且该变量的取值只有两个,0 或 1。例如抛硬币(不考虑硬币直立的情况)的概率分布就是伯努利分布。数学公式如下:
- P(x = 0) = 1 - λ
- P(x = 1) = λ
- 多项式分布:也叫分类分布,描述了一个具有 k 个不同状态的单个随机变量。这里的 k,是有限的数值,如果 k 为 2,那就变成了伯努利分布。
- P(x = k) = λ
- 二项式分布
- 泊松分布
常见的连续型数据分布模型有:
- 正态分布,也叫高斯分布,是最重要的一种。
- 均匀分布
- 指数分布
- 拉普拉斯分布
正态分布的数学公式为:

正态分布的分布图为:
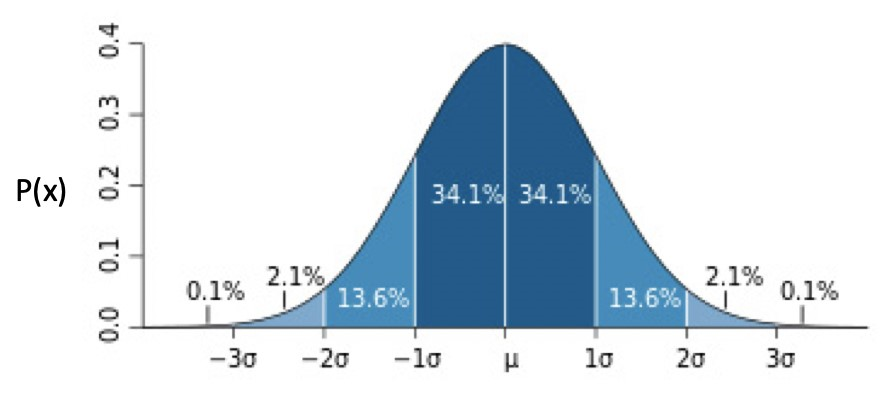
正态分布还可分为:
- 一元正态分布:此时 μ为 0,σ为 1。
- 多元正态分布。
数学期望,如果把“每次随机结果的出现概率”看做权重,那么期望就是所有结果的加权平均值。
方差表示的是随机变量的取值与其数学期望的偏离程度,方差越小意味着偏离程度越小,方差越大意味着偏离程度越大。
概率论研究的就是这些概率之间的转化关系。
2,贝叶斯定理
贝叶斯公式如下:
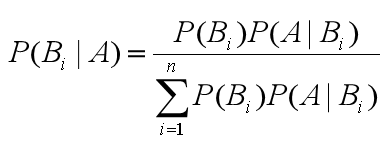
含义:
- 等号右边分子部分,
P(Bi)为先验概率,P(A|Bi)为条件概率。 - 等号右边整个分母部分为边缘概率。
- 等号左边
P(Bi|A)为后验概率,由先验概率,条件概率,边缘概率计算得出。
贝叶斯定理可用于分类问题,将其用在分类问题中时,可将上面的公式简化为:
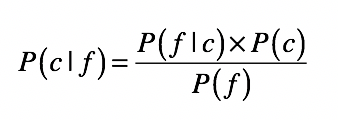
其中:
- c 表示一个分类,f 表示属性值。
- P(c|f) 表示在待分类样本中,出现属性值 f 时,样本属于类别 c 的概率。
- P(f|c) 是根据训练样本数据,进行统计得到的,分类 c 中出现属性 f 的概率。
- P(c ) 是分类 c 在训练数据中出现的概率。
- P(f) 是属性 f 在训练样本中出现的概率。
这就意味着,当我们知道一些属性特征值时,根据这个公式,就可以计算出所属分类的概率,最终所属哪个分类的概率最大,就划分为哪个分类,这就完成了一个分类问题。
贝叶斯推导
来看下贝叶斯公式是如何推导出来的。
如下图两个椭圆,左边为C,右边为F。
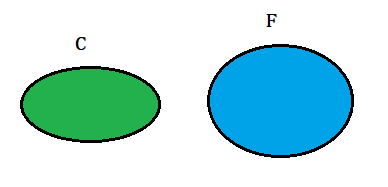
现在让两个椭圆产生交集:
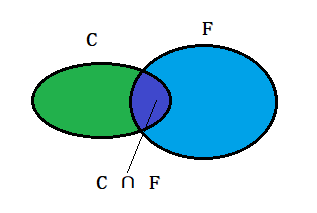
根据上图可知:在事件F 发生的条件下,事件C 发生的概率就是P(C ∩ F) / P(F),即:
P(C | F) = P(C ∩ F) / P(F)
可得到:
P(C ∩ F) = P(C | F) * P(F)
同理可得:
P(C ∩ F) = P(F | C) * P(C)
所以:
P(C ∩ F) = P(C | F) * P(F) = P(F | C) * P(C)P(C | F) = P(F | C) * P(C) / P(F)
3,朴素贝叶斯
假设我们现在有一个数据集,要使用贝叶斯定理,进行分类。特征有两个:f1,f2。现在要对数据F 进行分类,那我们需要求解:
P(c|F):表示数据F属于分类c的概率。
因为特征有 f1 与 f2,那么:
P(c|F) = P(c|(f1,f2))
对于分类问题,特征往往不止一个。如果特征之间相互影响,也就是f1 与f2 之间相互影响,那么P(c|(f1,f2)) 就不容易求解。
朴素贝叶斯在贝叶斯的基础上做了一个简单粗暴的假设,它假设多个特征之间互不影响,相互独立。
朴素的意思就是纯朴,简单。
用数学公式表示就是:
P(A, B) = P(A) * P(B)
实际上就是大学概率论中所讲的事件独立性,即事件A 与事件B 的发生互不干扰,相互独立。
那么,根据朴素贝叶斯,P(c|F) 的求解过程如下:
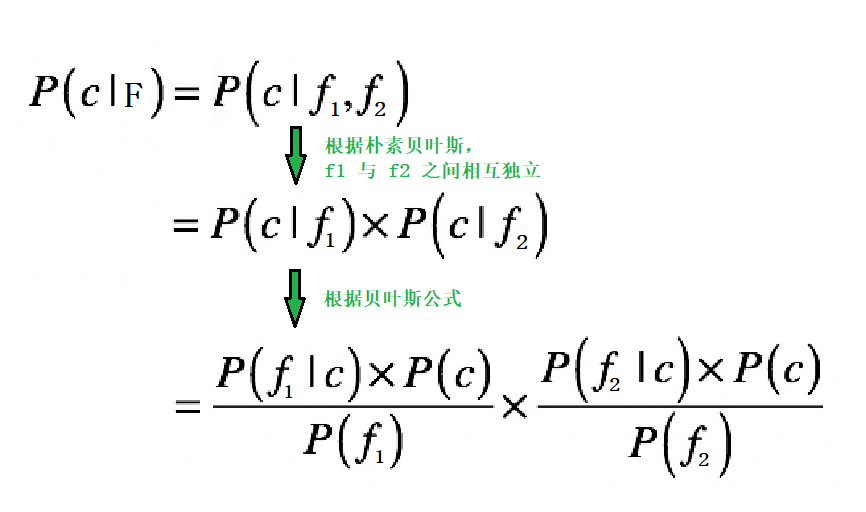
假设我们现在要分类的数据有两类:c1 和 c2。
那么对于数据F 的分类问题,我们就需要求解两个概率:P(c1|F) 和P(c2|F):
- 如果
P(c1|F) > P(c2|F),那么F属于c1类。 - 如果
P(c1|F) < P(c2|F),那么F属于c2类。
根据贝叶斯原理,我们可以得到:
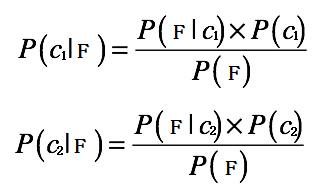
对于分类问题,我们的最终目的是分类,而不是真正的求解出P(c1|F) 和 P(c2|F) 的确切数值。
根据上面的公式,我们可以看到,等号右边的分母部分都是P(F):
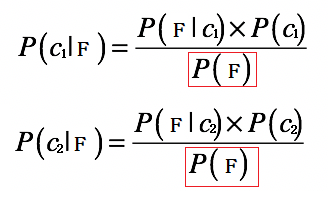
所以我们只需要求出P(F|c1) × P(c1) 和 P(F|c2) × P(c2),就可以知道P(c1|F) 和 P(c2|F) 哪个大了。
所以对于P(c|F) 可以进一步简化:

4,处理分类问题的一般步骤
用朴素贝叶斯原理,处理一个分类问题,一般要经过以下几个步骤:
- 准备阶段:
- 获取数据集。
- 分析数据,确定特征属性,并得到训练样本。
- 训练阶段:
- 计算每个类别概率
P(Ci)。 - 对每个特征属性,计算每个分类的条件概率
P(Fj|Ci)。 Ci代表所有的类别。Fj代表所有的特征。
- 计算每个类别概率
- 预测阶段:
- 给定一个数据,计算该数据所属每个分类的概率
P(Fj|Ci) * P(Ci)。 - 最终那个分类的概率大,数据就属于哪个分类。
- 给定一个数据,计算该数据所属每个分类的概率
5,用朴素贝叶斯分类
接下来我们来处理一个实际的分类问题,我们处理的是离散型数据。
5.1,准备数据集
我们的数据集如下:
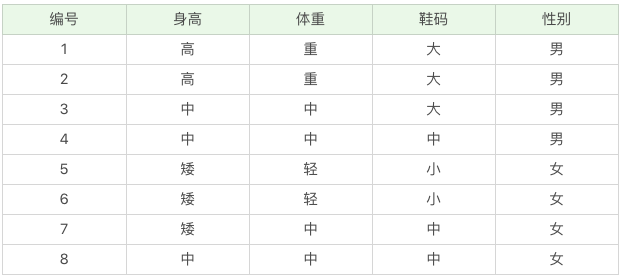
该数据集的特征集有身高,体重和鞋码,目标集为性别。
我们的目的是训练一个模型,该模型可以根据身高,体重和鞋码来预测所属的性别。
我们给定一个特征:
- 身高 = 高,用
F1表示。 - 体重 = 中,用
F2表示。 - 鞋码 = 中,用
F3表示。
要求这个特征是男还是女?(用C1 表示男,C2 表示女)也就是要求P(C1|F) 大,还是P(C2|F) 大?
# 根据朴素贝叶斯推导
P(C1|F)
=> P(C1|(F1,F2,F3))
=> P(C1|F1) * P(C1|F2) * P(C1|F3)
=> [P(F1|C1) * P(C1)] * [P(F2|C1) * P(C1)] * [P(F3|C1) * P(C1)]
P(C2|F)
=> P(C2|(F1,F2,F3))
=> P(C2|F1) * P(C2|F2) * P(C2|F3)
=> [P(F1|C2) * P(C2)] * [P(F2|C2) * P(C2)] * [P(F3|C2) * P(C2)]
5.2,计算P(Ci)
目标集共有两类:男和女,男出现4 次,女出现4 次,所以:
P(C1) = 4 / 8 = 0.5P(C2) = 4 / 8 = 0.5
5.3,计算P(Fj|Ci)
通过观察表格中的数据,我们可以知道:
# 性别为男的情况下,身高=高 的概率
P(F1|C1) = 2 / 4 = 0.5
# 性别为男的情况下,体重=中 的概率
P(F2|C1) = 2 / 4 = 0.5
# 性别为男的情况下,鞋码=中 的概率
P(F3|C1) = 1 / 4 = 0.25
# 性别为女的情况下,身高=高 的概率
P(F1|C2) = 0 / 4 = 0
# 性别为女的情况下,体重=中 的概率
P(F2|C2) = 2 / 4 = 0.5
# 性别为女的情况下,鞋码=中 的概率
P(F3|C2) = 2 / 4 = 0.5
5.4,计算P(Fj|Ci) * P(Ci)
上面我们已经推导过P(C1|F) 和 P(C2|F),下面可以求值了:
P(C1|F)
=> [P(F1|C1) * P(C1)] * [P(F2|C1) * P(C1)] * [P(F3|C1) * P(C1)]
=> [0.5 * 0.5] * [0.5 * 0.5] * [0.25 * 0.5]
=> 0.25 * 0.25 * 0.125
=> 0.0078125
P(C2|F)
=> [P(F1|C2) * P(C2)] * [P(F2|C2) * P(C2)] * [P(F3|C2) * P(C2)]
=> [0 * 0.25] * [0.5 * 0.5] * [0.5 * 0.5]
=> 0
最终可以看到 P(C1|F) > P(C2|F),所以该特征属于C1,即男性。
6,总结
可以看到,对于一个分类问题:给定一个数据F,求解它属于哪个分类? 实际上就是要求解F 属于各个分类的概率大小,即P(C|F)。
根据朴素贝叶斯原理,P(C|F) 与 P(F|C) * P(C) 正相关,所以最终要求解的就是P(F|C) * P(C)。这就将一个分类问题转化成了一个概率问题。
下篇文章会介绍如何使用朴素贝叶斯处理实际问题。
(本节完。)
推荐阅读:
欢迎关注作者公众号,获取更多技术干货。