LeetCode:Longest Valid Parentheses

           Given a string containing just the characters '(' and ')', find the

length of the longest valid (well-formed) parentheses substring.For "(()", the 

longest valid parentheses substring is "()", which has length = 2.

Another example is ")()())", where the longest valid parentheses substring 

is "()()", which has length = 4.

解题思路:

    这题能够用栈或者dp做，只是自己用栈写的O(N)的解法没有dp的快，所以说下dp的思路吧.

首先，看下状态的定义:

• dp[i]:表示选了第i个字符能组成的最长有效括号个数.

通过上面状态的定义。非常easy得出以下的状态转移方程:

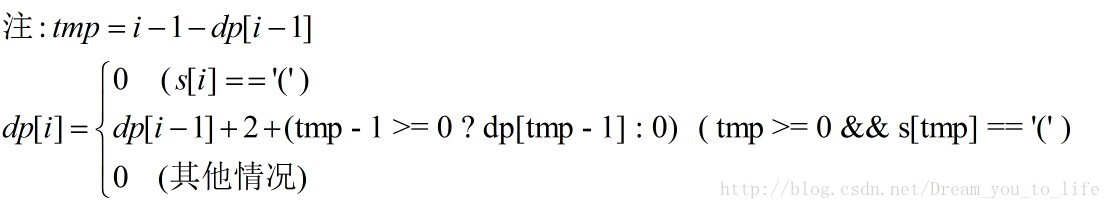
这里解释下第二个状态方程的得来，当s[i]=')'时，tmp表示的就是与s[i]相应的那个字符，假设其满足

条件(tmp>=0 && s[tmp]=='(')那么就说明tmp到i这部分是有效括号匹配。而tmp之前的也有可能存在有

效括号匹配。所以须要将两者相加，须要注意的是，边界的地方.

解题代码:

class Solution {
public:
    int longestValidParentheses(string s) 
    {
        int n = s.size(), dp[n];
        dp[0] = 0;
        for (int i = 1; i < n; ++i)
        {
            int tmp = i - 1 - dp[i - 1];
            if (s[i] == '(')
                dp[i] = 0;
            else if (tmp >= 0 && s[tmp] == '(')
                dp[i] = dp[i - 1] + 2 + (tmp - 1 >= 0 ?
 dp[tmp - 1] : 0);
            else
                dp[i] = 0;
        }
        return *max_element(dp, dp + n);
    }
};