[SCOI2016]萌萌哒

嘟嘟嘟


这题我连(O(n ^ 2))的都没想出来……
刚开始看到字符串就想SAM，然后发现连具体的串都没有，觉得再用字符串算法的话就有点扯了。


首先应该发现一点，如果然两个区间相等，实际上就是两个区间对应位置的数相等。所以我们把区间拆成一个个单独的位置，然后用并查集维护相等的位置集合即可。
那么答案就是9 * (联通块数量 - 1)，因为第一位不能为0.


修改复杂度(O(n))，查询复杂度也是(O(n))，只能得30分。
因为这题只有一次查询，所以想办法把修改改为(O(logn))，查询改为(O(nlogn))。
然后有人就想到了倍增。
(p[j][i])表示区间([i, i + (1 << j) - 1])所在的集合。这样修改的时候就跟倍增lca很像了，往后跳合并即可。
查询的时候就比较妙，就是把大区间的合并信息下传给小区间，就像下图一样：

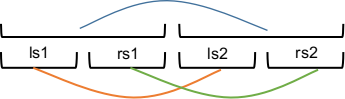
即两个大区间的左儿子和右儿子分别合并。（刚开始我理解成左右儿子都合并到大区间上……）
写的时候可以记录每一个区间的左右儿子是谁，就像这位的代码一样：学姐的代码
然后我从题解里发现了一个更简单的写法，详情参见下方代码。


实现的时候就是把并查集的所有操作都加一位。

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<vector>
#include<stack>
#include<queue>
using namespace std;
#define enter puts("") 
#define space putchar(' ')
#define Mem(a, x) memset(a, x, sizeof(a))
#define In inline
typedef long long ll;
typedef double db;
const int INF = 0x3f3f3f3f;
const db eps = 1e-8;
const int maxn = 1e5 + 5;
const int N = 17;
const ll mod = 1e9 + 7;
inline ll read()
{
  ll ans = 0;
  char ch = getchar(), last = ' ';
  while(!isdigit(ch)) last = ch, ch = getchar();
  while(isdigit(ch)) ans = (ans << 1) + (ans << 3) + ch - '0', ch = getchar();
  if(last == '-') ans = -ans;
  return ans;
}
inline void write(ll x)
{
  if(x < 0) x = -x, putchar('-');
  if(x >= 10) write(x / 10);
  putchar(x % 10 + '0');
}

int n, m;

int p[N + 2][maxn];
In void init()
{
  for(int i = 1; i <= n; ++i)
    for(int j = 0; j <= N; ++j) p[j][i] = i;
}
In int Find(int x, int k)
{
  return x == p[k][x] ? x : p[k][x] = Find(p[k][x], k);
}
In void merge(int x, int y, int k)
{
  int px = Find(x, k), py = Find(y, k);
  if(px ^ py) p[k][px] = py;
}

int main()
{
  freopen("2.in", "r", stdin);
  //freopen("ha.out", "w", stdout);
  n = read(), m = read();
  init();
  for(int i = 1; i <= m; ++i)
    {
      int l1 = read(), r1 = read(), l2 = read(), r2 = read();
      for(int j = N; j >= 0 ; --j)
	if((1 << j) <= r1 - l1 + 1)
	  {
	    merge(l1, l2, j);
	    l1 += (1 << j), l2 += (1 << j);
	  }
    }
  for(int j = N; j; --j)
    for(int i = 1; i + (1 << j) - 1 <= n; ++i)
      {
	merge(i, Find(i, j), j - 1);
	merge(i + (1 << (j - 1)), Find(i, j) + (1 << (j - 1)), j - 1);
      }
  int tot = 0; ll ans = 9;
  for(int i = 1; i <= n; ++i) if(Find(i, 0) == i) ++tot;
  for(int i = 1; i < tot; ++i) ans = ans * 10 % mod;
  write(ans), enter;
  return 0;
}