CF1338D Nested Rubber Bands

传送门


这题又是那种典型的cf题，代码难度不是很大，但得想半天。
可以先参考一下官方的题解，我感觉我以下的思路有一点混乱。


首先我们发现，相邻的两个点(u, v)肯定不能一同在答案序列中，但一个节点(u)相连的所有点可以在同一个答案序列中，只要把(u)画成一个很长的图形，和他相连的点画成一堆嵌套的圆即可，如下图：

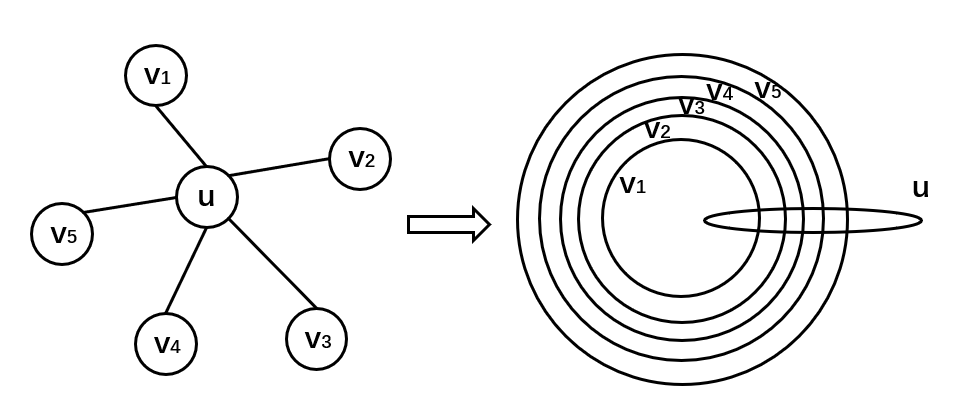
进一步可以发现，我们可以选一条链，链上的节点画成很长图形（以下称为“管道”），用于连接，和链相连的节点就可以画成一堆嵌套的圆。

而且，一定只能是一条链，一端不可能有分支。因为一旦有分支，分支上相连的点画出的圆必定会和其他分支上的“管道”相交，就不符合题目中相交的充要条件了。

但这还没完，还有一点在于，对于一条链，我们可以要么选择一个点相连的所有点，要么选择他本身，但一定不能连续选择两个本身点。这种构造就是把一个“管道”变成圆，然后下一个管道只和这个圆相交。而不能选择连续两个管道将其变成圆，在于相邻的点的图形必须相交。


综上，我们要做的就是，在树上选择一条简单路径，对于路径上的点，要么选择路径外和他相连的点，要么选择他自身，但不能连续选择两个路径上的点，求能选择的最多的点数。


而这件事，可以用树形dp实现。

令(dp[u][0/1])表示以(u)为端点的一条链，其中(u)没选/选了的情况下，总共选择的最多的点数。那么转移方程只用考虑和他的子节点(v)的关系，挺好写的：

[egin{align} dp[u][0] &= max { dp[v][0] - 1 + du[u] - 1, dp[v][1] + du[u] - 1}, \ dp[u][1] &= max { dp[v][0] - 1 + 1}. end{align} ]

而计算答案，是在递归过程中，计算每一个节点的dp值的同时，合并两条链来计算的。

这里有个小trick，在(u)的子树中，合并两条链实际上是(O(n^2))的，但是我们可以在用(v)更新(u)之前，将(dp[u])和(dp[v])合并，因为有以下等价式：

[max_{1leqslant i, j leqslant n} { x_i + x_j } = max_{i=1}^n { max_{j=1}^{i-1} {x_j } + x_i }. ]

(max_{j=1}^{i-1} {x_j })就是当前的(dp[u])，(x_i)就是枚举的(dp[v]).

而合并的式子，和dp的转移方程很像，就直接看代码吧。

#include<bits/stdc++.h> 
using namespace std;
#define enter puts("") 
#define space putchar(' ')
#define Mem(a, x) memset(a, x, sizeof(a))
#define In inline
#define forE(i, x, y) for(int i = head[x], y; ~i && (y = e[i].to); i = e[i].nxt)
typedef long long ll;
typedef double db;
const int INF = 0x3f3f3f3f;
const db eps = 1e-8;
const int maxn = 1e5 + 5;
In ll read()
{
	ll ans = 0;
	char ch = getchar(), las = ' ';
	while(!isdigit(ch)) las = ch, ch = getchar();
	while(isdigit(ch)) ans = (ans << 1) + (ans << 3) + ch - '0', ch = getchar();
	if(las == '-') ans = -ans;
	return ans;
}
In void write(ll x)
{
	if(x < 0) x = -x, putchar('-');
	if(x >= 10) write(x / 10);
	putchar(x % 10 + '0');
}
In void MYFILE()
{
#ifndef mrclr
	freopen(".in", "r", stdin);
	freopen(".out", "w", stdout);
#endif
}

int n, du[maxn];
struct Edge
{
	int nxt, to;
}e[maxn << 1];
int head[maxn], ecnt = -1;
In void addEdge(int x, int y)
{
	e[++ecnt] = (Edge){head[x], y};
	head[x] = ecnt;
}

int dp[maxn][2], ans = 0;
In void dfs(int now, int _f)
{
	dp[now][0] = du[now], dp[now][1] = 1;
	forE(i, now, v)
	{
		if(v == _f) continue;
		dfs(v, now);
		ans = max(ans, dp[now][0] + max(dp[v][0] - 2, dp[v][1] - 1));
		ans = max(ans, dp[now][1] + dp[v][0] - 1);
		dp[now][0] = max(dp[now][0], max(dp[v][0] - 2, dp[v][1] - 1) + du[now]);
		dp[now][1] = max(dp[now][1], dp[v][0]);
	}
}

int main()
{
//	MYFILE();
	Mem(head,- 1), ecnt = -1;
	n = read();
 	for(int i = 1; i < n; ++i)
 	{
 		int x = read(), y = read();
 		addEdge(x, y), addEdge(y, x);
 		du[x]++, du[y]++;
 	}
 	dfs(1, 0);
 	write(ans), enter;
	return 0;
}