LCA(Lowest Common Ancestor 最近公共祖先)定义如下:在一棵树中两个节点的LCA为这两个节点所有的公共祖先中深度最大的节点。
比如这棵树
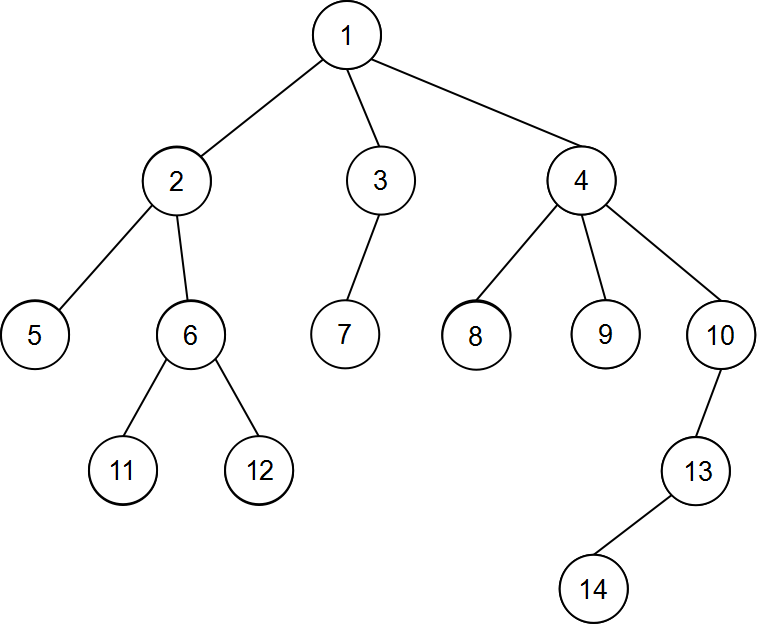
结点5和6的LCA是2,12和7的LCA是1,8和14的LCA是4。
这里讲一下将LCA转化成RMQ问题,进而用st表求解。
首先我们跑一遍dfs,并记录经过的每一个结点(包括回溯的时候),存到一个数组中,这样我就将树的问题转化成线性问题。
等下上图的树好像有些大
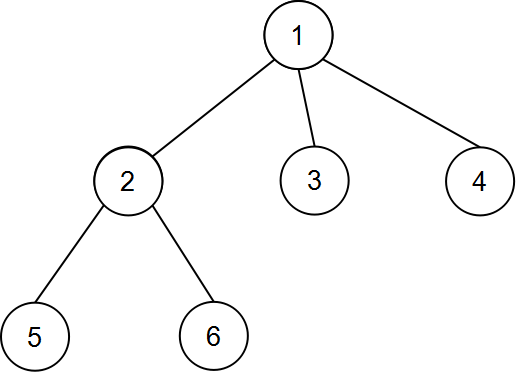
这就好多了。
然后就是dfs序列和深度序列
dfs序 1 2 5 2 6 2 1 3 1 4 1
dep序 1 2 3 2 3 2 1 2 1 2 1
根据dfs的性质,从node[u]遍历到node[v]的过程中,经过LCA(u, v)有且仅有一次,而且它的深度一定是区间[u, v]中是最小的,那么这就是一个显而易见的RMQ(静态区间最小值)问题了。
我们就以洛谷的板子为例,传送门:https://www.luogu.org/problemnew/show/P3379
这里的vis数组是用来处理无向图存两次边的
先写一个dfs序
1 vector<int>v[maxn]; 2 //node存的dfs序,dep深度序列,firs[s]指s第一次出现在dfs序中的位置 3 int dep[2 * maxn], node[2 * maxn], firs[maxn], vis[maxn]; 4 int p = 1; 5 void dfs(int s, int d) //s用来构造dfs序,d用来构造深度序列 6 { 7 vis[s] = 1; 8 dep[p] = d; node[p] = s; firs[s] = p++; 9 for(int i = 0; i < v[s].size(); ++i) 10 { 11 if(!vis[v[s][i]]) 12 { 13 dfs(v[s][i], d + 1); //孩子的深度肯定是父亲的深度+1 14 dep[p] = d; node[p++] = s; 15 } 16 } 17 }
然后考一个RMQ板子就行了
1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 #include<algorithm> 5 #include<cstring> 6 #include<vector> 7 using namespace std; 8 const int maxn = 5e5 + 5; 9 int n, m, s; 10 vector<int>v[maxn]; 11 //node存的dfs序,dep深度序列,firs[s]指s第一次出现在dfs序中的位置 12 int dep[2 * maxn], node[2 * maxn], firs[maxn], vis[maxn]; 13 int p = 1; 14 void dfs(int s, int d) //s用来构造dfs序,d用来构造深度序列 15 { 16 vis[s] = 1; 17 dep[p] = d; node[p] = s; firs[s] = p++; 18 for(int i = 0; i < v[s].size(); ++i) 19 { 20 if(!vis[v[s][i]]) 21 { 22 dfs(v[s][i], d + 1); //孩子的深度肯定是父亲的深度+1 23 dep[p] = d; node[p++] = s; 24 } 25 } 26 } 27 //pos[L][R]表示的是区间[L, R]中最小值在dfs序中的位置 28 int dp[2 * maxn][25], pos[2 * maxn][25], que[2 * maxn]; 29 void init() 30 { 31 int n = p - 1; 32 for(int i = 1; i <= n; ++i) {dp[i][0] = dep[i]; pos[i][0] = i;} 33 for(int j = 1; (1 << j) <= n; ++j) 34 for(int i = 1; i + (1 << j) - 1 <= n; ++i) 35 { 36 if(dp[i][j - 1] < dp[i + (1 << (j - 1))][j - 1]) 37 { 38 dp[i][j] = dp[i][j - 1]; pos[i][j] = pos[i][j - 1]; 39 } 40 else 41 { 42 dp[i][j] = dp[i + (1 << (j - 1))][j - 1]; pos[i][j] = pos[i + (1 << (j - 1))][j - 1]; 43 } 44 } 45 int k = 0; 46 for(int i = 1; i <= n; ++i) 47 { 48 if ((1 << k) <= i) k++; 49 que[i] = k - 1; 50 } 51 } 52 void query(int L, int R) 53 { 54 if (R < L) swap(L, R); 55 int k = que[R - L + 1]; 56 if(dp[L][k] < dp[R - (1 << k) + 1][k]) printf("%d ", node[pos[L][k]]); 57 else printf("%d ", node[pos[R - (1 << k) + 1][k]]); 58 return; 59 } 60 int main() 61 { 62 scanf("%d%d%d", &n, &m, &s); 63 for(int i = 1; i < n; ++i) 64 { 65 int a, b; scanf("%d%d", &a, &b); 66 v[a].push_back(b); v[b].push_back(a); 67 } 68 dfs(s, 1); 69 init(); 70 while(m--) 71 { 72 int a, b; scanf("%d%d", &a, &b); 73 query(firs[a], firs[b]); 74 } 75 return 0; 76 }