zoukankan html css js c++ java

20172327 2018-2019-1 《程序设计与数据结构》实验二：树实验报告

课程：《Java软件结构与数据结构》
班级：201723
姓名：马瑞蕃
学号：20172327
实验教师：王志强
实验日期：2018年11月7日-2018年11月11日
必修/选修：必修

一、实验内容：

实验二树-1-实现二叉树

参考教材p212,完成链树LinkedBinaryTree的实现（getRight,contains,toString,preorder,postorder）

用JUnit或自己编写驱动类对自己实现的LinkedBinaryTree进行测试

实验二树-2-中序先序序列构造二叉树

1.基于LinkedBinaryTree，实现基于（中序，先序）序列构造唯一一棵二㕚树的功能，
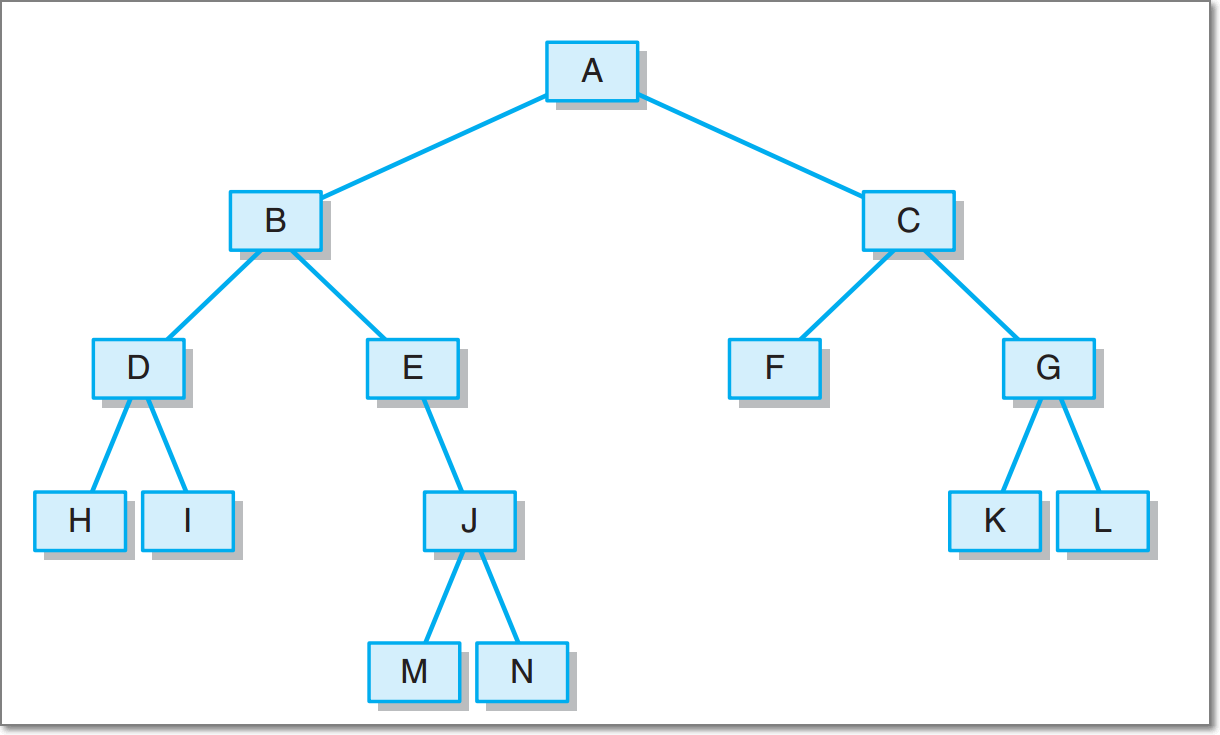
2.给出中序HDIBEMJNAFCKGL和后序ABDHIEJMNCFGKL,构造出附图中的树
3.用JUnit或自己编写驱动类对自己实现的功能进行测试

实验二树-3-决策树

1.自己设计并实现一颗决策树

实验二树-4-表达式树

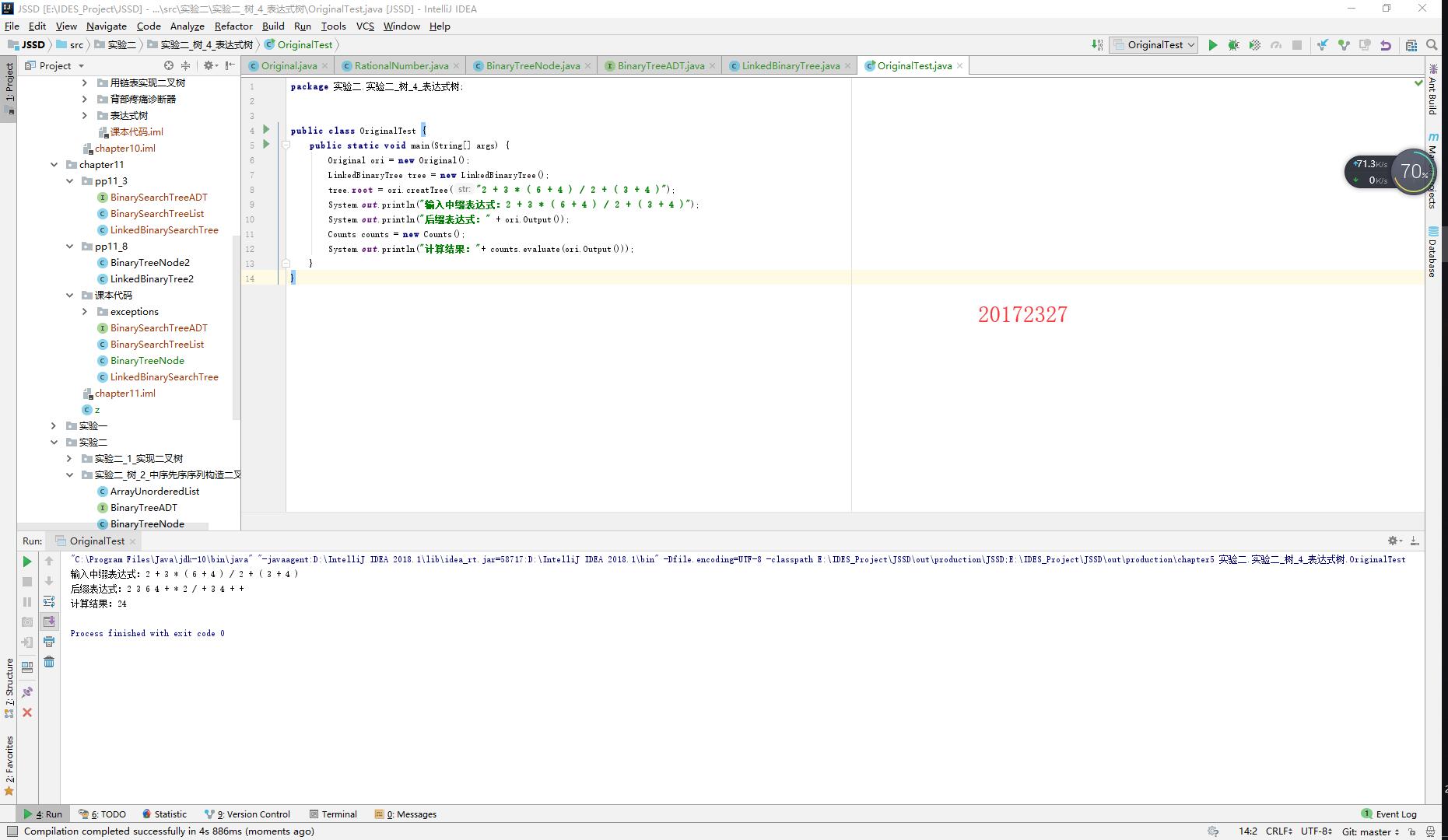
1.输入中缀表达式，使用树将中缀表达式转换为后缀表达式，并输出后缀表达式和计算结果（如果没有用树，则为0分）

实验二树-5-二叉查找树

1.完成PP11.3

实验二树-6-红黑树分析

参考http://www.cnblogs.com/rocedu/p/7483915.html对Java中的红黑树（TreeMap，HashMap）进行源码分析，并在实验报告中体现分析结果。
（C:Program FilesJavajdk-11.0.1libsrcjava.basejavautil）

二、实验过程及结果：

树-1-实现二叉树

要实现 LinkedBinaryTree 中的方法，首先要将结点类 BinaryTreeNode 补充完整。在结点类中，需要补充先序遍历和后序遍历的函数，由于这里用到了迭代器和递归的思路，所以直接参考中序遍历给出的函数即可：

    //为树的中序遍历返回一个迭代器
    public Iterator<T> iteratorInOrder() {
        ArrayUnorderedList<T> tempList = new ArrayUnorderedList<T>();
        inOrder(root, tempList);
        return new TreeIterator(tempList.iterator());
    }
    protected void inOrder(BinaryTreeNode<T> node, ArrayUnorderedList<T> tempList) {
        if (node != null) {
            inOrder(node.getLeft(), tempList);
            tempList.addToRear(node.getElement());
            inOrder(node.getRight(), tempList);
        }
    }

整左子树、右子树和根的访问顺序以及对应方法即可实现另外两种函数：

    //为树的前序遍历返回一个迭代器
    public Iterator<T> iteratorPreOrder() {
        ArrayUnorderedList<T> tempList = new ArrayUnorderedList<T>();
        preOrder(root, tempList);
        return new TreeIterator(tempList.iterator());
    }
    private void preOrder(BinaryTreeNode<T> node, ArrayUnorderedList<T> tempList) {
        if (node != null) {
            tempList.addToRear(node.getElement());
            inOrder(node.getLeft(), tempList);
            inOrder(node.getRight(), tempList);
        }
    }

    @Override
    //为树的后序遍历返回一个迭代器
    public Iterator<T> iteratorPostOrder() {
        ArrayUnorderedList<T> tempList = new ArrayUnorderedList<T>();
        postOrder(root, tempList);
        return new TreeIterator(tempList.iterator());
    }
    private void postOrder(BinaryTreeNode<T> node, ArrayUnorderedList<T> tempList) {
        if (node != null) {
            inOrder(node.getLeft(), tempList);
            inOrder(node.getRight(), tempList);
            tempList.addToRear(node.getElement());
        }
    }

实现了结点类之后，对应地去实现方法类 LinkedBinaryTree，方法类中需要补充的函数有：getRight,contains,isEmpty,toString,preorder,postorder.

getRight 方法可以参考给出的 getLeft 方法：

    //返回结点的左侧子结点
    public LinkedBinaryTree<T> getLeft() {
        return left;
    }
    //返回结点的右侧子结点
    public LinkedBinaryTree<T> getRight() {
        return right;
    }

contains 方法我主要考虑了根为空、和检测元素为空的情况，并对此做出条件判断即可：（如果根为空则会因 node 的初始值返回 false）

 public boolean contains(T target) {
        BTNode<T> node = null;
        boolean result = true;
        if(root != null)
            node = root.find(target);

        if(node == null)
            result = false;

        return result;
    }

isEmpty 方法的实现比较简单，但是我第一次做的时候，将判断条件写成了 root.count() == 0，
【注意】树结构不是链表，也不是数组，count方法是返回子树的结点数，所以开始就默认根结点存在了即count方法的返回值至少为1，所以当然不能用在isEmpty方法中。
这里直接判断根结点是否为空即可：

    //判断树是否为空
    @Override
    public boolean isEmpty() {
        return (root == null);
    }

toString 方法的思路与之前实现的数据结构（栈、队列）有些类似，注意这里要用到遍历方法，要用到递归，所以我用数组迭代类创建对象，之后层序遍历输出。我在实现这个方法时出现了很多报错，借助IDEA的提示，才成功解决了问题：

//打印树
    @Override
    public String toString(){
        UnorderedListADT<BinaryTreeNode<T>> nodes = new ArrayUnorderedList<BinaryTreeNode<T>>();
        UnorderedListADT<Integer> levelList = new ArrayUnorderedList<Integer>();

        BinaryTreeNode<T> current;
        String result = "";
        int printDepth = this.getHeight();
        int possibleNodes = (int) Math.pow(2, printDepth + 1);
        int countNodes = 0;

        nodes.addToRear(root);
        Integer currentLevel = 0;
        Integer previousLevel = -1;
        levelList.addToRear(currentLevel);

        while (countNodes < possibleNodes) {
            countNodes = countNodes + 1;
            current = nodes.removeFirst();
            currentLevel = levelList.removeFirst();
            if (currentLevel > previousLevel) {
                result = result + "

";
                previousLevel = currentLevel;
                for (int j = 0; j < ((Math.pow(2, (printDepth - currentLevel))) - 1); j++)
                    result = result + "  ";
            } else {
                for (int i = 0; i < ((Math.pow(2,
                        (printDepth - currentLevel + 1)) - 1)); i++) {
                    result = result + "  ";
                }
            }
            if (current != null) {
                result = result + (current.getElement()).toString();
                nodes.addToRear(current.getLeft());
                levelList.addToRear(currentLevel + 1);
                nodes.addToRear(current.getRight());
                levelList.addToRear(currentLevel + 1);
            } else {
                nodes.addToRear(null);
                levelList.addToRear(currentLevel + 1);
                nodes.addToRear(null);
                levelList.addToRear(currentLevel + 1);
                result = result + "  ";
            }
        }
        return result;
    }

preorder 和 postorder 方法只需参考给出的 inorder 方法改一下遍历方式就行：（这三者的遍历方式都是按子树进行的，所以框架相同）

    @Override
    //为树的前序遍历返回一个迭代器
    public Iterator<T> iteratorPreOrder() {
        ArrayUnorderedList<T> tempList = new ArrayUnorderedList<T>();
        preOrder(root, tempList);
        return new TreeIterator(tempList.iterator());
    }
    private void preOrder(BinaryTreeNode<T> node, ArrayUnorderedList<T> tempList) {
        if (node != null) {
            tempList.addToRear(node.getElement());
            inOrder(node.getLeft(), tempList);
            inOrder(node.getRight(), tempList);
        }
    }

    @Override
    //为树的后序遍历返回一个迭代器
    public Iterator<T> iteratorPostOrder() {
        ArrayUnorderedList<T> tempList = new ArrayUnorderedList<T>();
        postOrder(root, tempList);
        return new TreeIterator(tempList.iterator());
    }
    private void postOrder(BinaryTreeNode<T> node, ArrayUnorderedList<T> tempList) {
        if (node != null) {
            inOrder(node.getLeft(), tempList);
            inOrder(node.getRight(), tempList);
            tempList.addToRear(node.getElement());
        }
    }

链接

树-2-中序先序序列构造二叉树

步骤：
（1）确定树的根结点；（先序遍历的第一个结点就是二叉树的根）
（2）求解树的子树；（找到根在中序遍历的位置，位置左边就是二叉树的左孩子，位置右边是二叉树的右孩子，如果根结点左边或右边为空，那么该方向子树为空；如果根节点左边和右边都为空，那么根节点已经为叶结点）
（3）对二叉树的左、右孩子分别进行步骤（1）（2），直到求出二叉树的结构为止。

链接

树-3-决策树

这个实验算是最令人愉悦的一个吧！可以自己设计问题和答案，课本上也有一个示例代码可以参考，这样思路上就比较容易了。
决策树需要注意的就是不要搞混左子树和右子树的对象，在传递元素时可以参考书中的格式，先定义元素，再定义对应类型的树，之后再将元素依次实例化并填入构建的子树，根据回答迭代输出问题，直到只剩下最后一层叶结点，输出判定结果即可：

链接

树-4-表达式树

使用树来表示算术表达式，我知道一部分，又参考了利用Java实现表达式二叉树，但还是没能实现输入后缀，输出中缀的情况。这里的表达式结果输出我理解为中序输出，至于输入我想使用后缀表达式，我继续查找相关资料，并参考了其中的部分代码：

public class Original extends LinkedBinaryTree{
    public BinaryTreeNode creatTree(String str){
        StringTokenizer tokenizer = new StringTokenizer(str);
        String token;
        ArrayList<String> operList = new ArrayList<>();

        ArrayList<LinkedBinaryTree> numList = new ArrayList<>();
        while (tokenizer.hasMoreTokens()){
            token = tokenizer.nextToken();
            if(token.equals("(")){
                String str1 = "";
                while (true){
                    token = tokenizer.nextToken();
                    if (!token.equals(")"))
                        str1 += token + " ";
                    else break;
                }
                LinkedBinaryTree S = new LinkedBinaryTree();
                S.root = creatTree(str1);
                numList.add(S);
            }
            if(as(token)){
                operList.add(token);
            }else if(md(token)){
                LinkedBinaryTree left = numList.remove(numList.size()-1);
                String A = token;
                token = tokenizer.nextToken();
                if(!token.equals("(")) {
                    LinkedBinaryTree right = new LinkedBinaryTree(token);
                    LinkedBinaryTree node = new LinkedBinaryTree(A, left, right);
                    numList.add(node);
                }else {
                    String str1 = "";
                    while (true){
                        token = tokenizer.nextToken();
                        if (!token.equals(")"))
                            str1 += token + " ";
                        else break;
                    }
                    LinkedBinaryTree S = new LinkedBinaryTree();
                    S.root = creatTree(str1);
                    LinkedBinaryTree node = new LinkedBinaryTree(A,left,S);
                    numList.add(node);
                }
            }else
                numList.add(new LinkedBinaryTree(token));
        }
        while(operList.size()>0){
            LinkedBinaryTree left = numList.remove(0);
            LinkedBinaryTree right = numList.remove(0);
            String oper = operList.remove(0);

            LinkedBinaryTree node = new LinkedBinaryTree(oper,left,right);
            numList.add(0,node);
        }
        root = (numList.get(0)).root;

        return root;
    }

    private boolean as(String token){
        return (token.equals("+")||
                token.equals("-"));
    }

    private boolean md(String token){
        return (token.equals("*")||
                token.equals("/"));
    }

    public String Output(){
        String result = "";
        ArrayList<String> list = new ArrayList<>();
        root.postorder(list);
        for(String i : list){
            result += i+" ";
        }
        return result;
    }
}

链接

树-5-二叉查找树

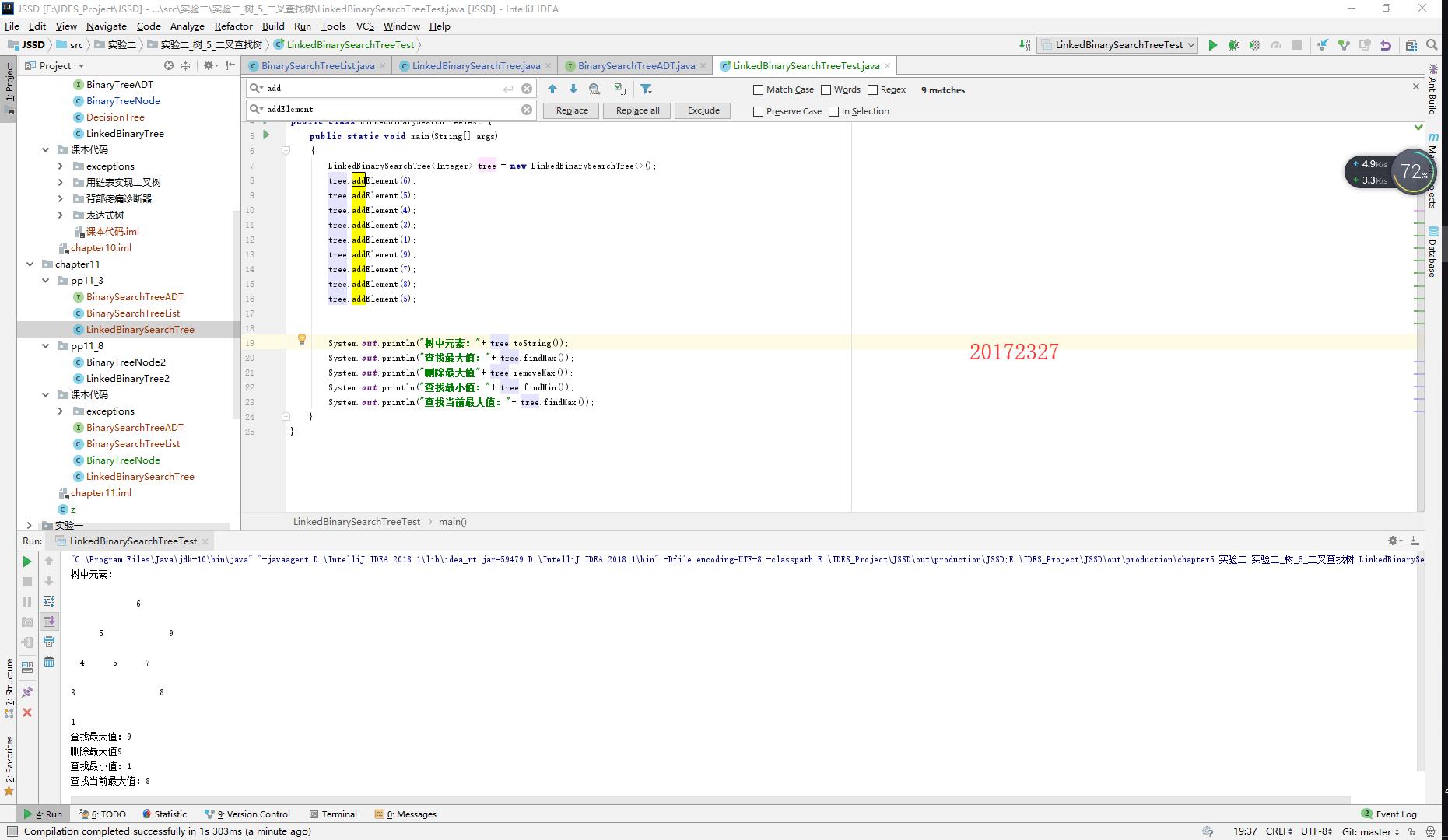
这个实验相对容易些，要求实现二叉查找树中的方法 findMin 和 findMax，这两种方法无非是找出二叉查找树中的特殊元素，所以可以从遍历方式上考虑。由于二叉查找树的最小元素始终位于整棵树左下角最后一个左子树的第一个位置，所以就可以直接返回这个元素的位置，至于怎么获取这个元素就可以使用之前的遍历方法，二叉查找树的最小元素是中序遍历的第一个元素，而后序遍历就不一定，其他的遍历方式也不行。于是就返回中序遍历后的第一个元素即可。
二叉查找树中最大元素的查找过程同理，还是采用中序遍历最保险，需要使用两次强转：

    //返回二进制搜索中最小值的元素树.它不会从二进制搜索树中删除该节点。如果此树为空, 则抛出 EmptyCollectionException。
    // @return 最小值的元素
    // @throws EmptyCollectionException 如果树是空的
    public T findMin() throws EmptyCollectionException 
    {
        T result = null;

        if (isEmpty())
            throw new EmptyCollectionException("LinkedBinarySearchTree");
        else {
            if (root.left == null) {
                result = root.element;
                //root = root.right;
            } else {
                BinaryTreeNode<T> parent = root;
                BinaryTreeNode<T> current = root.left;
                while (current.left != null) {
                    parent = current;
                    current = current.left;
                }
                result = current.element;
                //parent.left = current.right;
            }

            //modCount--;
        }

        return result;

    }

    //返回在二进制文件中具有最高值的元素搜索树。 它不会从二进制文件中删除节点搜索树。 如果此树为空, 则抛出 EmptyCollectionException。
    // @return 具有最高值的元素
    // @throws EmptyCollectionException 如果树是空的
    public T findMax() throws EmptyCollectionException 
    {
        T result = null;

        if (isEmpty())
            throw new EmptyCollectionException("LinkedBinarySearchTree");
        else {
            if (root.right == null) {
                result = root.element;
                //root = root.left;
            } else {
                BinaryTreeNode<T> parent = root;
                BinaryTreeNode<T> current = root.right;
                while (current.right != null) {
                    parent = current;
                    current = current.right;
                }
                result = current.element;
                //parent.right = current.left;
            }

            //modCount--;
        }

        return result;

    }

链接

树-6-红黑树分析

这两个类的源码比较长，我只针对其中的几个方法进行了分析。
首先说说红黑树：参考 http://www.cnblogs.com/skywang12345/p/3245399.html
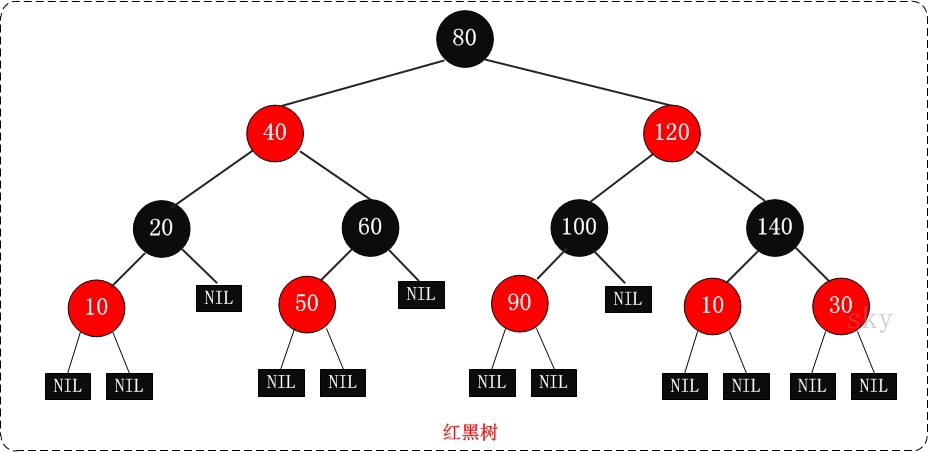
红黑树，即 R-B Tree，全称是Red-Black Tree，它一种特殊的二叉查找树。红黑树的每个结点上都有存储位表示结点的颜色，可以是红(Red)或黑(Black)。
红黑树的特性：
（1）每个结点或者是黑色，或者是红色。
（2）根结点是黑色。
（3）每个叶结点（NIL）是黑色。【注意：这里叶结点，是指为空(NIL或NULL)的叶结点！】
（4）如果一个结点是红色的，则它的子节点必须是黑色的。
（5）从一个结点到该结点的子孙结点的所有路径上包含相同数目的黑结点。
【注意：特性(3)中的叶结点，是只为空(NIL或null)的结点。
特性(5)，确保没有一条路径会比其他路径长出俩倍。因而，红黑树是相对是接近平衡的二叉树。】
红黑树示意图：
TreeMap类：

public class TreeMap<K,V>
    extends AbstractMap<K,V>
    implements NavigableMap<K,V>, Cloneable, java.io.Serializable
----------------------------------------------------------------
//TreeMap 是一个有序的key-value集合，它是通过红黑树实现的。
//TreeMap 继承于AbstractMap，所以它是一个Map，即一个key-value集合。
//TreeMap 实现了NavigableMap接口，意味着它支持一系列的导航方法。比如返回有序的key集合。
//TreeMap 实现了Cloneable接口，意味着它能被克隆。
//TreeMap 实现了java.io.Serializable接口，意味着它支持序列化。

firstEntry()和getFirstEntry()方法：

public Map.Entry<K,V> firstEntry() {
    return exportEntry(getFirstEntry());
}
final Entry<K,V> getFirstEntry() {
    Entry<K,V> p = root;
    if (p != null)
        while (p.left != null)
            p = p.left;
    return p;
}

firstEntry() 和 getFirstEntry() 都是用于获取第一个节点。firstEntry() 是对外接口；getFirstEntry() 是内部接口。而且，firstEntry() 是通过 getFirstEntry() 来实现的。

HashMap类：
初始容量与加载因子是影响HashMap的两个重要因素：

public HashMap(int initialCapacity, float loadFactor)

初始容量默认值：

 /**
     * The default initial capacity - MUST be a power of two.
     */
    static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16

加载因子默认值：

/**
     * The load factor used when none specified in constructor.
     */
    static final float DEFAULT_LOAD_FACTOR = 0.75f;

containsValue类：

 public boolean containsValue(Object value) {
        Node<K,V>[] tab; V v;
        if ((tab = table) != null && size > 0) {
            for (int i = 0; i < tab.length; ++i) {
                for (Node<K,V> e = tab[i]; e != null; e = e.next) {
                    if ((v = e.value) == value ||
                        (value != null && value.equals(v)))
                        return true;
                }
            }
        }
        return false;
    }

如果在map中包含对应的特定的键值则返回true，否则返回false。

三、实验过程中遇到的问题和解决过程

问题出现了好多，但我都解决了，忘截图了，所以这地我也不知道写点啥。

四、感悟

通过这次实验，我发现我对这段时间树的学习并部扎实，有些基本的还是记不住，在逻辑推理的过程中，遇到的麻烦也比较多。这次实验让我知道了，最近的不足，也让我决定抽出更多时间去学习Java。

参考资料

查看全文

相关阅读:
VS项目如何运用svn的忽略列表
 Hyper-V如何应用新的网卡
 android:Layout_weight的深刻理解
 使用WebView出现web page not available
如何在android模拟器中导入搜狗输入法？
ASP.Net生成静态HTML页
 微软URLRewriter.dll的url重写的简单使用(实现伪静态)
servlet中获得tomcat项目根目录的绝对路径
 Log4j使用指南
 处理URL传递中文乱码问题

原文地址：https://www.cnblogs.com/mrf1209/p/9942644.html

20172327 2018-2019-1 《程序设计与数据结构》实验二：树实验报告

20172327 2018-2019-1 《程序设计与数据结构》实验二：树实验报告

一、实验内容：

实验二 树-1-实现二叉树

实验二 树-2-中序先序序列构造二叉树

实验二 树-3-决策树

实验二 树-4-表达式树

实验二 树-5-二叉查找树

实验二 树-6-红黑树分析

二、实验过程及结果：

树-1-实现二叉树

树-2-中序先序序列构造二叉树

树-3-决策树

树-4-表达式树

树-5-二叉查找树

树-6-红黑树分析

三、实验过程中遇到的问题和解决过程

四、感悟

参考资料

实验二树-1-实现二叉树

实验二树-2-中序先序序列构造二叉树

实验二树-3-决策树

实验二树-4-表达式树

实验二树-5-二叉查找树

实验二树-6-红黑树分析