[poj] 1389 Area of Simple Polygons

原题

线段树+扫描线

对于这样一个不规则图形，我们要求他的面积有两种方法，割和补。
补显然不行，因为补完你需要求补上去的内部分不规则图形面积……
那么怎么割呢？
像这样：

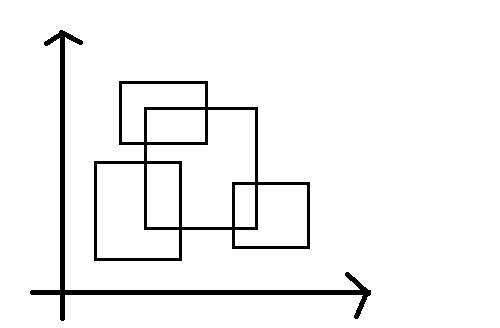
我们就转化成了无数个矩形的和。要想求这些矩形的面积，也就是底成高。因为我们并不懂什么二维线段树，所以我们就用“扫描线”（从左到右的更新计算）。
不妨把y轴当做一个线段树，然后维护哪些位置被覆盖了，直到下一条更新，所增加的面积就是被覆盖位置（高）和这两个距离的差（底）的乘积。
Eg:

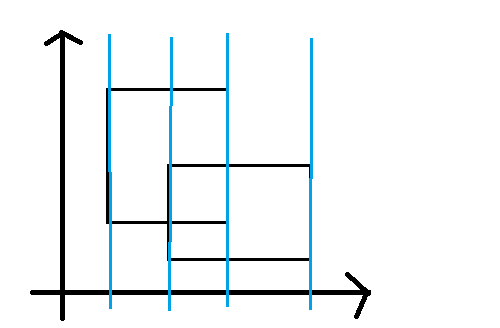
我们第一次更新建了第一条边的树，第二次更新时就可以增加这么多的长度。

然后我们考虑这样一个情况，如果某个位置被覆盖了很多次怎么办，显然我们线段树的维护是不能将它重复计算多次的，那么我们就加一个cover数组，来记录当前区间被覆盖过多少次，那样在做下面这样的更新时就不会出错。

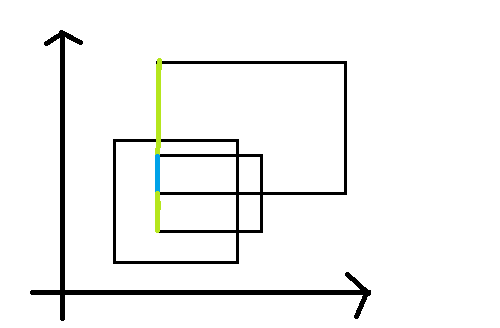
接下来来理解代码把～！

#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 1010
#define M 60010
using namespace std;
int x1,y1,x2,y2,s[4*M],cov[4*M],ans,tot,mxy;
struct hhh
{
    int x,yf,yb,k;
    bool operator < (const hhh &b) const
	{
	    if (x==b.x) return k<b.k;
	    return x<b.x;
	}
}a[2*N];

int read()
{
    int ans=0,fu=1;
    char j=getchar();
    for (;(j<'0' || j>'9') && j!='-';j=getchar()) ;
    if (j=='-') j=getchar();
    for (;j>='0' && j<='9';j=getchar()) ans*=10,ans+=j-'0';
    return ans*fu;
}

void modify(int i,int l,int r,int x,int y,int k)
{
    if (x<=l && y>=r)
    {
	cov[i]+=k;
	if (cov[i]) s[i]=r-l+1;
	else if (l==r) s[i]=0;
	else s[i]=s[i*2]+s[i*2+1];
    }
    else
    {
	int mid=(l+r)>>1;
	if (x<=mid) modify(i*2,l,mid,x,y,k);
	if (y>mid) modify(i*2+1,mid+1,r,x,y,k);
	if (!cov[i]) s[i]=s[i*2]+s[i*2+1];
    }
}

int main()
{
    while (~scanf("%d%d%d%d",&x1,&y1,&x2,&y2))
    {
	mxy=0;
	tot=1;
	if (x1==-1 && y1==-1 && x2==-1 && y2==-1) break;
	memset(cov,0,sizeof(cov));
	memset(s,0,sizeof(s));
	while (1)
	{
	    if (x1==-1 && y1==-1 && x2==-1 && y2==-1) break;
	    mxy=max(mxy,y2);
	    a[tot].x=x1;a[tot].yf=y1;a[tot].yb=y2;a[tot++].k=1;
	    a[tot].x=x2;a[tot].yf=y1;a[tot].yb=y2;a[tot++].k=-1;
	    scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
	}
	sort(a+1,a+tot);
	ans=0;
	modify(1,0,mxy,a[1].yf+1,a[1].yb,a[1].k);
	for (int i=2;i<tot;i++)
	{
	    ans+=s[1]*(a[i].x-a[i-1].x);
	    modify(1,0,mxy,a[i].yf+1,a[i].yb,a[i].k);
	}
	printf("%d
",ans);
    }
    return 0;
}