行列式基本知识及代码实现

参考链接：https://cloud.tencent.com/developer/article/1594842

另外参考了张宇的考研视频。

1. 基本知识

一、行列式的定义与性质

1. 几何法定义

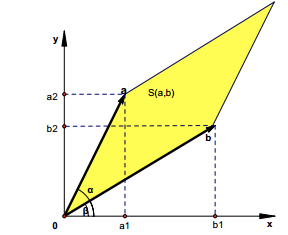
二阶行列式的值为平时四边形的面积。

     

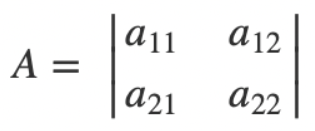
 面积表示如下：

 

 三阶行列式表示的是平行六面体的体积。

依次类推：n阶行列式表示的就是n个n维向量为邻边的n维图形的体积。

可以把行列式看作一个算式。

2. 逆序法定义

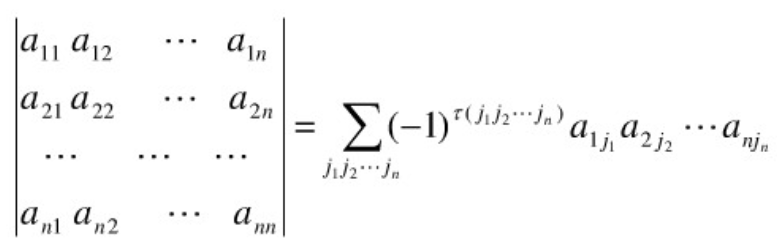
有以下相关点：

（1）展开后有n!个项；

（2）每项取自不同行、不同列n个元素的乘积；

（3）行下标顺序排列后，每项前乘以。

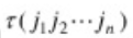称作j1 j2 ... jn的逆序数。

逆序数的概念：平时我们说的1 2叫做顺序，4 3就叫做逆序（也就是大的数在前，小的数在后）。

如t(6 4 1 2 3 5)的逆序数就是8。

3. 展开法定义

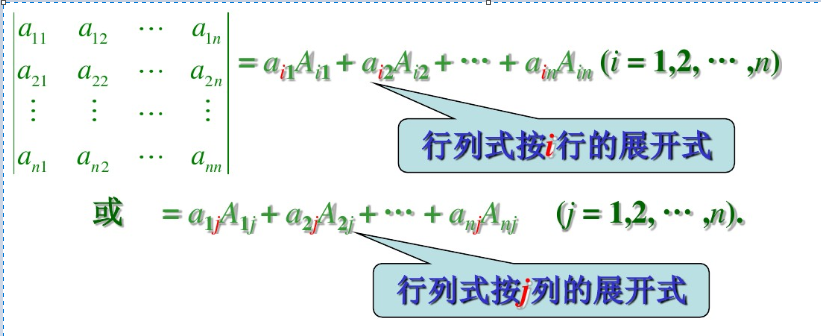
 行列式等于它的任一行（列）的各元素与其对应的代数余子式乘积之和。

2. python代码实现

python的numpy库提供了用于进行行列式计算的库函数，使用起来很方便。

代码实现如下：

# encoding: utf-8

import os
import numpy as np
from numpy.linalg import det


def test_2d_linalg():
    D2 = np.arange(4).reshape(2, 2)
    val = det(D2)
    print (D2)
    print (val)


def test_3d_linalg():
    D3 = np.arange(9).reshape(3, 3)
    val = det(D3)
    print (D3)
    print (val)


def test_multiD_linalg():
    data = [[1, 2, 3, 4, 5], [2, 2, 2, 1, 1], [3, 1, 2, 4, 5], [1, 1, 1, 2, 2], [4, 3, 1, 5, 0]]
    d5 = np.array(data)
    print (d5)
    print (det(d5))


if __name__ == "__main__":

    test_2d_linalg()

    test_3d_linalg()

    test_multiD_linalg()

输出结果：

[[0 1]
 [2 3]]
-2.0
[[0 1 2]
 [3 4 5]
 [6 7 8]]
0.0
[[1 2 3 4 5]
 [2 2 2 1 1]
 [3 1 2 4 5]
 [1 1 1 2 2]
 [4 3 1 5 0]]
26.99999999999999

总结：对如何用工具或代码生成数学公式还不了解，导致这篇博客写得很僵硬。