1. Conditional Probability and Bayes
Source: https://www.analyticsvidhya.com/blog/2017/09/naive-bayes-explained/

2. Assumptions made by naive bayes
The solution to using Bayes Theorem for a conditional probability classification model is to simplify the calculation.
The Bayes Theorem assumes that each input variable is dependent upon all other variables. This is a cause of complexity in the calculation. We can remove this assumption and consider each input variable as being independent from each other.
This changes the model from a dependent conditional probability model to an independent conditional probability model and dramatically simplifies the calculation.
Naive Bayes is a classification algorithm for binary (two-class) and multiclass classification problems. It is called Naive Bayes or idiot Bayes because the calculations of the probabilities for each class are simplified to make their calculations tractable.
Fundemental assumptions are: Each feature is
- Independent
- Equal(say, given the same influence)
Note: The assumptions made by Naïve Bayes are generally not correct in real-world situations. The independence assumption is never correct but often works well in practice. Hence the name ‘Naïve’. (source: https://levelup.gitconnected.com/naïve-bayes-algorithm-everything-you-need-to-know-9bf3104b78e5)
条件独立假设等于说是用于分类的特征在类确定的条件下都是条件独立的,这一假设使得朴素贝叶斯法变得简单, 但有时会牺牲一定的分类准确率。
3. Examples
Task 1: traffic jam (https://programmerbackpack.com/naive-bayes-classifier-explained/)
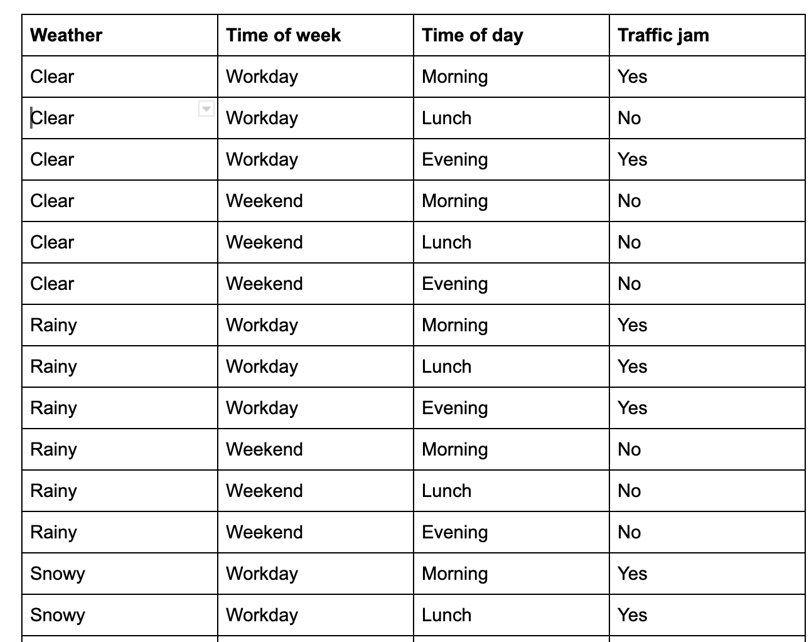
X = [Clear, Workday, Morning]
Y = [y1, y2]where y1 is the probability that there's no traffic jam and y2 is the probability that there is a traffic jam.
P(Y=y|X=(x1, x2, ..., xm))
since not dependent,
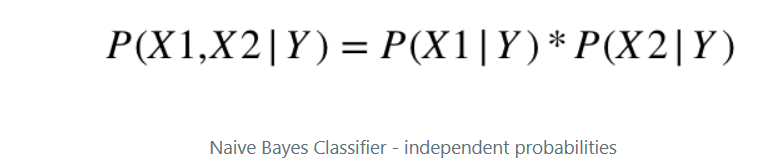
so we have

Task 2: Identify texts
Simple input, source: https://monkeylearn.com/blog/practical-explanation-naive-bayes-classifier/

- The first thing we need to do when creating a machine learning model is to decide what to use as features.
In this case though, we don’t even have numeric features. We just have text.
So what do we do? Simple! We use word frequencies.
That is, we ignore word order and sentence construction, treating every document as a set of the words it contains.
Our features will be the counts of each of these words. Even though it may seem too simplistic an approach, it works surprisingly well.
-
Now we need to transform the probability we want to calculate into something that can be calculated using word frequencies.
For this, we will use some basic properties of probabilities, and Bayes’ Theorem.

-
Naive
So here comes the Naive part: we assume that every word in a sentence is independent of the other ones.

to
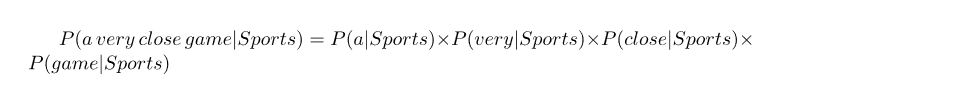
对于并没有出现在text里面的word,By using something called Laplace smoothing: we add 1 to every count so it’s never zero.
得到的results:
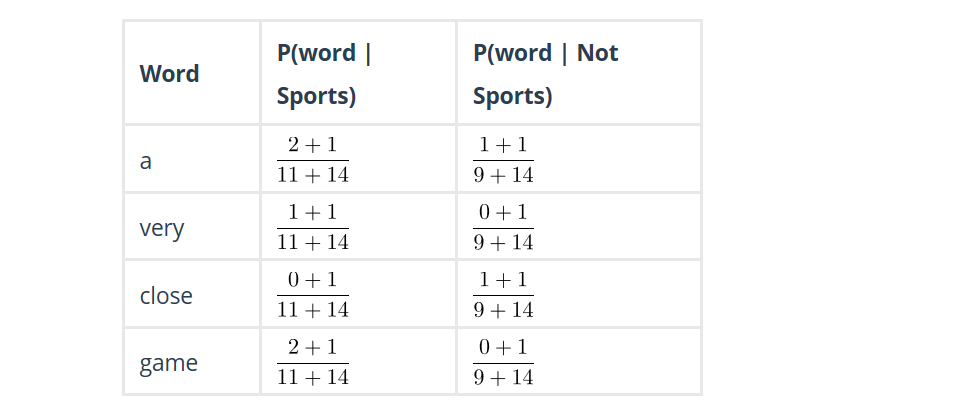
最后比较:

对于continuous data 就要用到Gaussian了
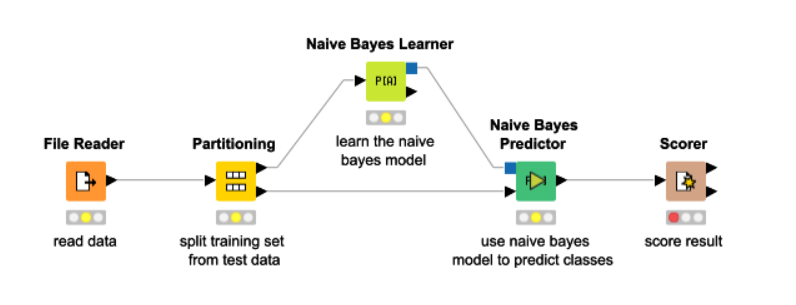
A general flow
本章概要
-
典型的生成学习方法,由训练数据学习联合概率分布P(X|Y),再求得厚颜概率分布P(Y|X).
-
概率估计方法可以是极大似然估计(满足独立同分布的假设)或贝叶斯估计
-
基本假设是条件独立性
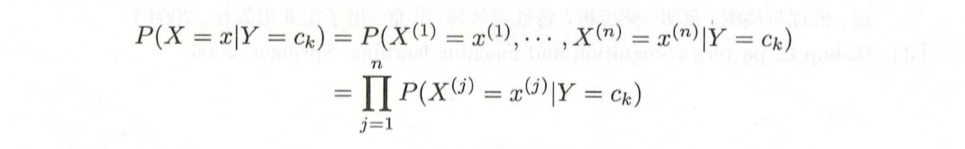
-
利用贝叶斯定理和学到的联合概率模型进行分类预测
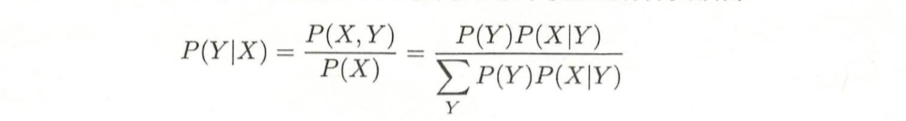
将输入x分到后验概率最大的类 y
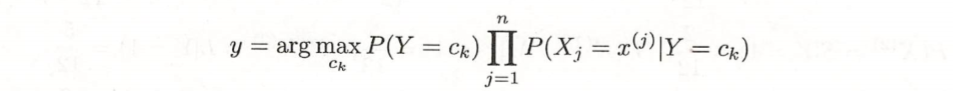
后验概率最大等价于0-1损失函数时的期望风险最小化。