Kaggle：Home Credit Default Risk 特征工程构建及可视化（2）

    博主在之前的博客 Kaggle：Home Credit Default Risk 数据探索及可视化（1） 中介绍了 Home Credit Default Risk 竞赛中一个优秀 kernel 关于数据的探索及可视化的工作，本篇博客将围绕如何构建特征工程展开叙述，原文链接地址：Start Here: A Gentle Introduction

1 简介

    特征工程是指一个基因过程，可以涉及特征构建：从现有数据中添加新特征和特征选择：仅选择最重要的特征或其他降维方法。我们可以使用许多技术来创建特征和选择特征。
    当我们开始使用其他数据源时，我们会做很多功能工程，本次，我们只会尝试两种简单的功能构建方法：

• 多项式特征
• 领域知识功能

2 特征工程构建

2.1 多项式特征

    一个简单的特征构造方法称为多项式特征。例如，我们可以创建变量EXT_SOURCE_1 ^ 2和EXT_SOURCE_2 ^ 2以及变量，例如EXT_SOURCE_1 x EXT_SOURCE_2，EXT_SOURCE_1 x EXT_SOURCE_2 ^ 2，EXT_SOURCE_1 ^ 2 x EXT_SOURCE_2 ^ 2等等。这些由多个单独变量组合而成的特征被称为交互项，因为它们捕捉变量之间的交互作用。换句话说，虽然两个变量本身可能不会对目标产生强烈的影响，但将它们组合成单个交互变量可能会显示与目标的关系。统计模型中通常使用交互项来捕捉多个变量的影响，但我没有看到它们在机器学习中经常使用。尽管如此，我们可以尝试一些看看他们是否可以帮助我们的模型预测客户是否会偿还贷款。
       Jake VanderPlas 在他的优秀着作 Python for Data Science 中为那些想要了解更多信息的人写了多项式特征。

    在下面的代码中，我们使用EXT_SOURCE变量和DAYS_BIRTH变量创建多项式特征。Scikit-Learn有一个称为PolynomialFeatures 的有用类，可以创建多项式和交互项达到指定的程度。我们可以使用3度来查看结果（当我们创建多项式特征时，我们希望避免使用过高的度数，这是因为特征的数量随着度数指数级地变化，并且因为我们可能遇到问题过拟合）。

# Make a new dataframe for polynomial features
poly_features = app_train[['EXT_SOURCE_1', 'EXT_SOURCE_2', 'EXT_SOURCE_3', 'DAYS_BIRTH', 'TARGET']]
poly_features_test = app_test[['EXT_SOURCE_1', 'EXT_SOURCE_2', 'EXT_SOURCE_3', 'DAYS_BIRTH']]

# imputer for handling missing values
from sklearn.preprocessing import Imputer
imputer = Imputer(strategy = 'median')

poly_target = poly_features['TARGET']

poly_features = poly_features.drop(columns = ['TARGET'])

# Need to impute missing values
poly_features = imputer.fit_transform(poly_features)
poly_features_test = imputer.transform(poly_features_test)

from sklearn.preprocessing import PolynomialFeatures
                                  
# Create the polynomial object with specified degree
poly_transformer = PolynomialFeatures(degree = 3)

# Train the polynomial features
poly_transformer.fit(poly_features)

# Transform the features
poly_features = poly_transformer.transform(poly_features)
poly_features_test = poly_transformer.transform(poly_features_test)
print('Polynomial Features shape: ', poly_features.shape)

这创造了相当多的新功能。 要获取名称，我们必须使用多项式特性 get_feature_names 方法。

poly_transformer.get_feature_names(input_features = ['EXT_SOURCE_1', 'EXT_SOURCE_2', 'EXT_SOURCE_3', 'DAYS_BIRTH'])[:15]

有35个功能提升到3级和互动条件。 现在，我们可以看到这些新功能是否与目标相关。

# Create a dataframe of the features 
poly_features = pd.DataFrame(poly_features, 
                             columns = poly_transformer.get_feature_names(['EXT_SOURCE_1', 'EXT_SOURCE_2', 
                                                                           'EXT_SOURCE_3', 'DAYS_BIRTH']))

# Add in the target
poly_features['TARGET'] = poly_target

# Find the correlations with the target
poly_corrs = poly_features.corr()['TARGET'].sort_values()

# Display most negative and most positive
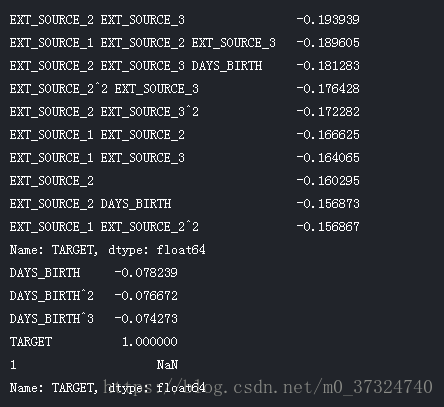
print(poly_corrs.head(10))
print(poly_corrs.tail(5))

下图是原始特征相关性系数排序图：

    与原始特征相比，几个新变量与目标的相关性更大（以绝对幅度表示）。 当我们构建机器学习模型时，我们可以尝试使用和不使用这些功能来确定它们是否真的有助于模型学习。

    我们将这些功能添加到培训和测试数据的副本中，然后评估具有和不具有功能的模型。 很多次机器学习，要知道一种方法是否可行，唯一的方法就是尝试一下！

# Put test features into dataframe
poly_features_test = pd.DataFrame(poly_features_test, 
                                  columns = poly_transformer.get_feature_names(['EXT_SOURCE_1', 'EXT_SOURCE_2', 
                                                                                'EXT_SOURCE_3', 'DAYS_BIRTH']))

# Merge polynomial features into training dataframe
poly_features['SK_ID_CURR'] = app_train['SK_ID_CURR']
app_train_poly = app_train.merge(poly_features, on = 'SK_ID_CURR', how = 'left')

# Merge polnomial features into testing dataframe
poly_features_test['SK_ID_CURR'] = app_test['SK_ID_CURR']
app_test_poly = app_test.merge(poly_features_test, on = 'SK_ID_CURR', how = 'left')

# Align the dataframes
app_train_poly, app_test_poly = app_train_poly.align(app_test_poly, join = 'inner', axis = 1)

# Print out the new shapes
print('Training data with polynomial features shape: ', app_train_poly.shape)
print('Testing data with polynomial features shape:  ', app_test_poly.shape)

2.2 领域知识特征

    也许把这种“领域知识”称为不完全正确，因为我不是信用专家，但也许我们可以称之为“尝试应用有限的金融知识”。 在这种思维框架下，我们可以制作一些功能，试图捕捉我们认为可能对于客户是否违约的贷款很重要。 在这里我将使用由 Aguiar 的这个脚本启发的五个特性：

• CREDIT_INCOME_PERCENT：信贷金额相对于客户收入的百分比
• ANNUITY_INCOME_PERCENT：贷款年金相对于客户收入的百分比
• CREDIT_TERM：以月为单位的付款期限（因为年金是应付的每月金额
• DAYS_EMPLOYED_PERCENT：相对于客户年龄所用天数的百分比

app_train_domain = app_train.copy()
app_test_domain = app_test.copy()

app_train_domain['CREDIT_INCOME_PERCENT'] = app_train_domain['AMT_CREDIT'] / app_train_domain['AMT_INCOME_TOTAL']
app_train_domain['ANNUITY_INCOME_PERCENT'] = app_train_domain['AMT_ANNUITY'] / app_train_domain['AMT_INCOME_TOTAL']
app_train_domain['CREDIT_TERM'] = app_train_domain['AMT_ANNUITY'] / app_train_domain['AMT_CREDIT']
app_train_domain['DAYS_EMPLOYED_PERCENT'] = app_train_domain['DAYS_EMPLOYED'] / app_train_domain['DAYS_BIRTH']

app_test_domain['CREDIT_INCOME_PERCENT'] = app_test_domain['AMT_CREDIT'] / app_test_domain['AMT_INCOME_TOTAL']
app_test_domain['ANNUITY_INCOME_PERCENT'] = app_test_domain['AMT_ANNUITY'] / app_test_domain['AMT_INCOME_TOTAL']
app_test_domain['CREDIT_TERM'] = app_test_domain['AMT_ANNUITY'] / app_test_domain['AMT_CREDIT']
app_test_domain['DAYS_EMPLOYED_PERCENT'] = app_test_domain['DAYS_EMPLOYED'] / app_test_domain['DAYS_BIRTH']

3 特征工程可视化

    我们应该在图形中直观地探索这些领域知识变量。 对于所有这些，我们将制作与目标值相同的 KDE 图（核密度估计图）。

plt.figure(figsize = (12, 20))
# iterate through the new features
for i, feature in enumerate(['CREDIT_INCOME_PERCENT', 'ANNUITY_INCOME_PERCENT', 'CREDIT_TERM', 'DAYS_EMPLOYED_PERCENT']):
    
    # create a new subplot for each source
    plt.subplot(4, 1, i + 1)
    # plot repaid loans
    sns.kdeplot(app_train_domain.loc[app_train_domain['TARGET'] == 0, feature], label = 'target == 0')
    # plot loans that were not repaid
    sns.kdeplot(app_train_domain.loc[app_train_domain['TARGET'] == 1, feature], label = 'target == 1')
    
    # Label the plots
    plt.title('Distribution of %s by Target Value' % source)
    plt.xlabel('%s' % source); plt.ylabel('Density');
    
plt.tight_layout(h_pad = 2.5)