递归算法举例

递归是一种解决问题的方法，将问题分解为更小的子问题，直到得到一个足够小的问题可以被很简单的解决。通常递归涉及函数调用自身。递归允许我们编写优雅的解决方案，解决可能很难编程的问题。

1 递归算法的三定律

在介绍递归思想的简单例子前，我们先了解下递归算法的三个重要的定律：
1.1 递归算法必须具有基本情况。
1.2 递归算法必须改变其状态并向基本情况靠近。
1.3 递归算法必须以递归方式调用自身。

2 计算整数列表和

假设没有 while 循环或 for 循环。你将如何计算整数列表的总和？可以使用以下的简化序列来计算最终的和。

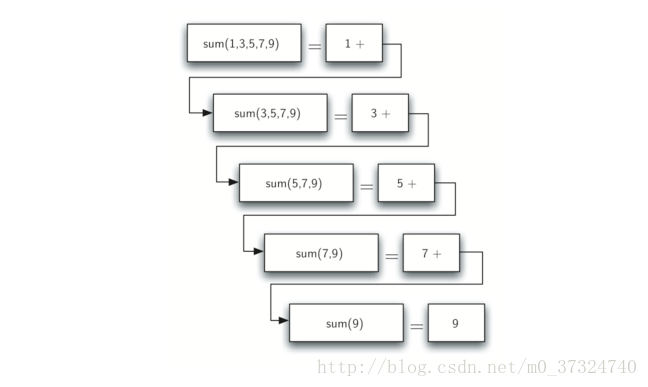
把这一系列的调用想象成一系列的简化。 每次我们进行递归调用时，我们都会解决一个较小的问题，直到达到问题不能减小的程度。下图展示了对列表[1,3,5,7,9] 求和所需的一系列递归调用。

python实现代码如下：

def listsum(numList):
   if len(numList) == 1:
        return numList[0]
   else:
        return numList[0] + listsum(numList[1:])

print(listsum([1,3,5,7,9]))

3 整数转换为任意进制字符串

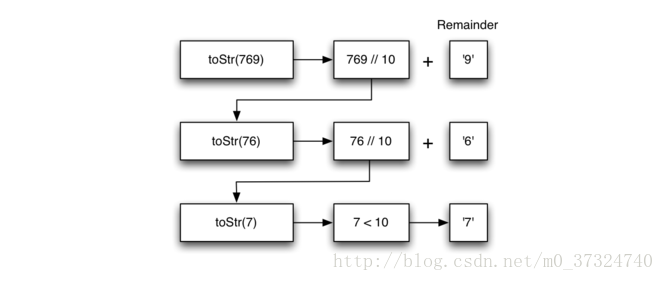
首先思考基本情况是什么？

如果我们将数字 769 分成三个单个位数字，7，6 和 9，那么将其转换为字符串很简单。数字小于 10 听起来像一个好的基本情况。并且用除法的数学运算似乎可以减少一个数字。余数除法为我们提供了一个明确的方向。

知道我们的基本情况是什么意味着整个算法将分成三个部分：
1. 将原始数字减少为一系列单个位数字。
2. 使用查找将单个位数字数字转换为字符串。
3. 将单个位字符串连接在一起以形成最终结果。

操作思路如下所示：

python实现代码如下：

def toStr(n,base):
   convertString = "0123456789ABCDEF"
   if n < base:
      return convertString[n]
   else:
      return toStr(n//base,base) + convertString[n%base]

print(toStr(1453,16))

4 栈帧实现递归

在上个例子中，假设不是将递归调用的结果与来自 convertString 的字符串拼接到 toStr，而是利用栈实现结果，该怎么做呢？
我们修改了算法，以便在进行递归调用之前将字符串入栈。此修改的算法的代码如下（关于栈的知识请参见我之前的博文：http://blog.csdn.net/m0_37324740/article/details/78830136）：

from pythonds.basic.stack import Stack

rStack = Stack()

def toStr(n,base):
    convertString = "0123456789ABCDEF"
    while n > 0:
        if n < base:
            rStack.push(convertString[n])
        else:
            rStack.push(convertString[n % base])
        n = n // base
    res = ""
    while not rStack.isEmpty():
        res = res + str(rStack.pop())
    return res

print(toStr(1453,16))

栈帧还为函数使用的变量提供了一个作用域。 即使我们重复地调用相同的函数，每次调用都会为函数本地的变量创建一个新的作用域。

参考资料：《problem-solving-with-algorithms-and-data-structure-using-python》
http://www.pythonworks.org/pythonds