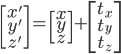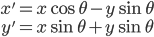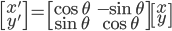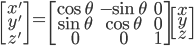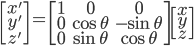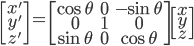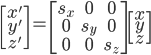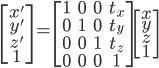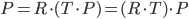计算机三维图形学中,一个基本的任务是如何描述三维空间中一个物体位置的变化,也就是如何 描述物体的运动。通常情况下,物体位置的变化包含三个基本的变化:平移、旋转和缩放,物体的运动也可以用这三个基本的运动形态的组合来描述。
图形学中物体运动的数学表述是:将点的初始位置坐标P0映射到经过平移、旋转、绽放后的新位置P1的过程。
平移:
平移就是在原始的三维空间坐标点上分别加上对应方向上的平移量:
旋转:
旋转分为两类:在二维平面和三维空间中的旋转。
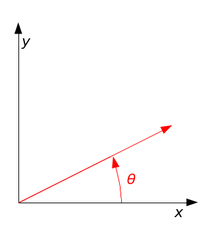
二维平面上的旋转:
相对坐标注原点旋转角度θ:
以矩阵形式表述:
扩展到三维空间,先看简单的绕某一个坐标轴旋转的情况。
绕Z轴旋转:
绕X轴旋转:
绕Y轴旋转:
三维空间中绕指定的任意轴旋转变换可以分解为分别绕三个坐标轴的旋转变换和一个平移变换的叠加。
缩放变换是三个维度上分别乘一个缩放系数:
总结以上,可以看到变换后的坐标点除了平移变换是在原始坐标上加上一个平移向量外,旋转、缩放都是在原始坐标点上乘以一个变换矩阵。
为了把平移变换也统一成矩阵相乘的形式,引入了齐次坐标。齐次坐标就是将一个原来是N维的向量用一个N+1维向量来表示 。在齐次坐标中用4个分量来表示三维空间中的一个点,前三个分量跟普通三维坐标一样,第四个分量设置为1。
在齐次坐标下,平移变换可以表述为:
这样,在齐次坐标系下,三维空间的运动一一平移、旋转、缩放在形式上都统一为左乘一个变换矩阵的形式。
考察一个物体的运动,先进行一次平移,再进行一次旋转,两个运动可以表述为:
R*T也是一个4*4的变换矩阵,这个变换包含了一次平移和一次旋转的叠加。
推广到更复杂的变换,只需要在当前R*T矩阵上依次左乘上对应的变换矩阵,最终得到的变换矩阵包含了物体所有变换的叠加,而这一系列的变换只需要用初始坐标左乘上这个最终的变换矩阵就可以实现,这个矩阵就是“模型矩阵”。
例如对于三维空间中的一条直线,直线经过点(x0,y0,z0),并且方向为(a,b,c),则一个物体绕该直线旋转θ角度的运动变换可以分解为:
- 平移(-x,-y,-z)平移到原点
- 绕x轴旋转角度p使指定的旋转轴在x-z平面上
- 绕y轴旋转角度q使指定的旋转轴与z轴重合
- 绕z轴旋转角度 绕y轴旋转角度-q
- 绕x轴旋转角度-p
- 平移(x,y,z )
综上可以看到,模型矩阵描述了三维空间物体的一系列变换的信息。在物体为刚体模型(刚体是在运动中和受力作用后,形状和大小不变,而且内部各点的相对位置不变的物体)的情况下,物体的所有顶点通过左乘模型矩阵,就可以实现物体的指定运动,所以模型矩阵大大降低了运动模型的复杂度。
模型视图矩阵
在模型矩阵中,关心的是物体在运动之后在世界坐标系下位置坐标点的变化。更加普遍的情况是,我们更加关心物体相对于观察者的位置变化,而不仅仅是关于世界坐标系下的变化。例如观察者在一辆运动着的汽车中观察另一辆相向而行的汽车的变换,这时候观察者和被观察的物体都在运动。这种观察者也在移动的情况,在现实世界中更加普遍。这也增加了确定运动模型的复杂度。
所幸的是,我们可以从另一个角度看待这个问题,即观察者的位置和方向发生变化时(这个变换可以用一个模型矩阵来表述),可以看做是被观察的物体进行了观察者运动相反的运动,即需要在模型矩阵的基础上再左乘一个观察者变换矩阵的逆矩阵,这个逆矩阵称为“视图矩阵”,而这个视图矩阵跟模型矩阵相乘得到的矩阵就是所谓的“模型视图矩阵”。
物体左乘模型视图矩阵后获得的新的位置(形状),描述 的是当观察者和物体都在运动时,物体在观察者眼中坐标点(形状)的变化。
数学 就是这么奇妙,它先把一个很简单问题复杂化,然后再把它简单化,以彰显其牛逼之处。