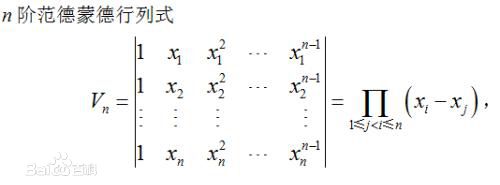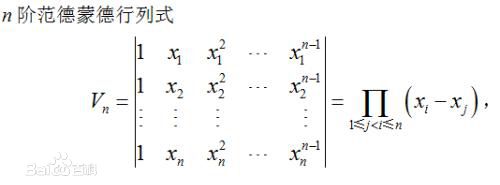
- 第 1 列的全部的 1,其实可视为,各个数的 0 次幂;
- 最后计算乘积时,是右侧的减去左侧,下侧的减去上侧的;
0. 范德蒙行列式的证明
数学归纳法,D2 显然成立,当 Dn−1 也成立时,Dn 是否成立?
Dn=∣∣∣∣∣∣∣∣1a1a21⋮an−111a2a22⋮an−121a3a23⋮an−13………⋱…1ana2n⋮an−1n∣∣∣∣∣∣∣∣
然后对 Dn 进行整理,从最后一行开始,rn:=rn−a1⋅rn−1(下一行 := 下一行 - a1上一行),因此往上:
Dn==∣∣∣∣∣∣∣∣100⋮01a2−a1a22−a2a1⋮an−12−an−22a11a3−a1a23−a3a1⋮an−13−an−23a1………⋱…1an−a1a2n−ana1⋮an−1n∣∣∣∣∣∣∣∣=(a2−a1)(a3−a1)⋯(an−a1)Π2≤j<i≤n(xi−xj)
得证;
1. 镶边法计算准范德蒙行列式
试计算如下行列式:
∣∣∣∣∣∣1aa2a41bb2b41cc2c41dd2d4∣∣∣∣∣∣
长得太像范德蒙行列式了,做如下镶边:
∣∣∣∣∣∣∣∣1aa2a3a41bb2b3b41cc2c3c41dd2d3d41xx2x3x4∣∣∣∣∣∣∣∣
因此整个行列式的值为:
(x−a)(x−b)(x−c)(x−d)(d−a)(d−b)(d−c)(c−a)(c−b)(b−a),此时,我们仅看 x3 项的系数(负的原行列式的值),(a+b+c+d)(d−a)(d−b)(d−c)(c−a)(c−b)(b−a)