相交弦定理的证明需要用到圆周角定理。
1. 圆周角定理
- 圆周角定理:同(等)弧所对圆周角相等;
2. 相交弦定理
相交弦定理:指圆内的两条相交弦,被交点分成的两条线段长的积相等。 或:经过圆内一点引两条弦,各弦被这点所分成的两线段的积相等;
几何语言描述:
若圆内任意弦AB、弦CD交于点P
则 PA·PB=PC·PD(相交弦定理)
相交线定理的证明:
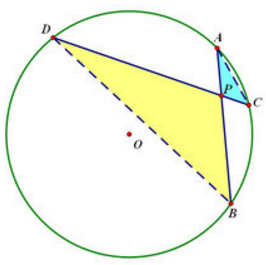
证明:连结AC,BD
由圆周角定理的推论,得∠A=∠D,∠C=∠B。(圆周角推论2: 同(等)弧所对圆周角相等.)
∴△PAC∽△PDB
∴PA∶PD=PC∶PB,PA·PB=PC·PD
注:其逆定理可作为证明圆的内接四边形的方法. P点若选在圆内任意一点更具一般性。其逆定理也可用于证明四点共圆。