其计算方法能够分为三类：
（1）基于区域或者基于特征的匹配方法；
（2）基于频域的方法；
（3）基于梯度的方法；
简单来说，光流是空间运动物体在观測成像平面上的像素运动的“瞬时速度”。
光流的研究是利用图像序列中的像素强度数据的时域变化和相关性来确定各自像素位置的“运动”。研究光流场的目的就是为了从图片序列中近似得到不能直接得到的运动场。
光流法的前提如果：
（1）相邻帧之间的亮度恒定。
（2）相邻视频帧的取帧时间连续，或者，相邻帧之间物体的运动比較“微小”；
（3）保持空间一致性；即，同一子图像的像素点具有同样的运动
这里有两个概念须要解释：
运动场，事实上就是物体在三维真实世界中的运动；
光流场，是运动场在二维图像平面上的投影。
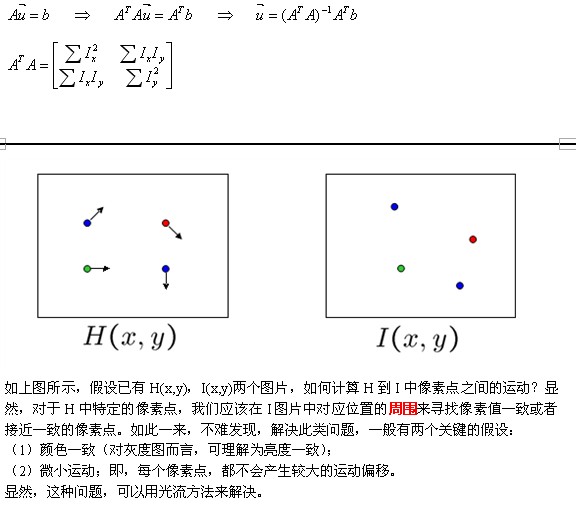
如上图所看到的。H中的像素点(x,y)在I中的移动到了(x+u,y+v)的位置，偏移量为(u,v)。
光流法用于目标检測的原理：给图像中的每一个像素点赋予一个速度矢量，这样就形成了一个运动矢量场。在某一特定时刻，图像上的点与三维物体上的点一一相应，这样的相应关系能够通过投影来计算得到。依据各个像素点的速度矢量特征，能够对图像进行动态分析。假设图像中没有运动目标。则光流矢量在整个图像区域是连续变化的。
当图像中有运动物体时。目标和背景存在着相对运动。运动物体所形成的速度矢量必定和背景的速度矢量有所不同。如此便能够计算出运动物体的位置。
须要提醒的是，利用光流法进行运动物体检測时。计算量较大，无法保证实时性和有用性。
光流法用于目标跟踪的原理：
（1）对一个连续的视频帧序列进行处理；
（2）针对每个视频序列。利用一定的目标检測方法。检測可能出现的前景目标；
（3）假设某一帧出现了前景目标，找到其具有代表性的关键特征点（能够随机产生，也能够利用角点来做特征点）；
（4）对之后的随意两个相邻视频帧而言，寻找上一帧中出现的关键特征点在当前帧中的最佳位置，从而得到前景目标在当前帧中的位置坐标；
（5）如此迭代进行。便可实现目标的跟踪；
IxVx+IyVy+It=0;
非常直观的讲，如果推断一个视频的相邻两帧I、J在某局部窗体w上是一样的，则在窗体w内有：I(x, y, t) = J(x', y', t+τ)。亮度恒定的如果(如果1)即为了保证其等号成立不受亮度的影响，如果2是为了保证KLT可以找到点。如果3则为下面原因如果（即对于同一个窗体中，全部点的偏移量都相等）：
在窗体w上，全部(x, y)都往一个方向移动了(dx, dy)，从而得到(x', y')，即t时刻的(x, y)点在t+τ时刻为(x+dx, y+dy)。所以寻求匹配的问题可化为对下面的式子寻求最小值。或叫做最小化下面式子：
用积分来表示上述式子，以上式子可等效为：
这个式子的含义，即找到两副图像中，在W窗体中，I、J的差异。当中I以x-d/2为中心。J以x+d/2为中心，w/2为半径的一个矩形窗体间的差异，好吧，结合我们微积分的知识。函数ε(d)要取得最小值。这个极值点的导数一定为0，即
的值为0，由泰勒展开的性质：
能够得到：
于是，问题转化为：
当中：
从而，问题即为：
=>
即其等式可看作为：
当中，Z为一个2*2的矩阵，e为一个2*1的向量，
为了要使d可以得到解。则Z须要满足条件，即Z*Z'矩阵可逆，当中Z'为Z矩阵的转置(ZT)。在普通情况下，角点具有这种特点。