下面的三道题都属于入门难度。
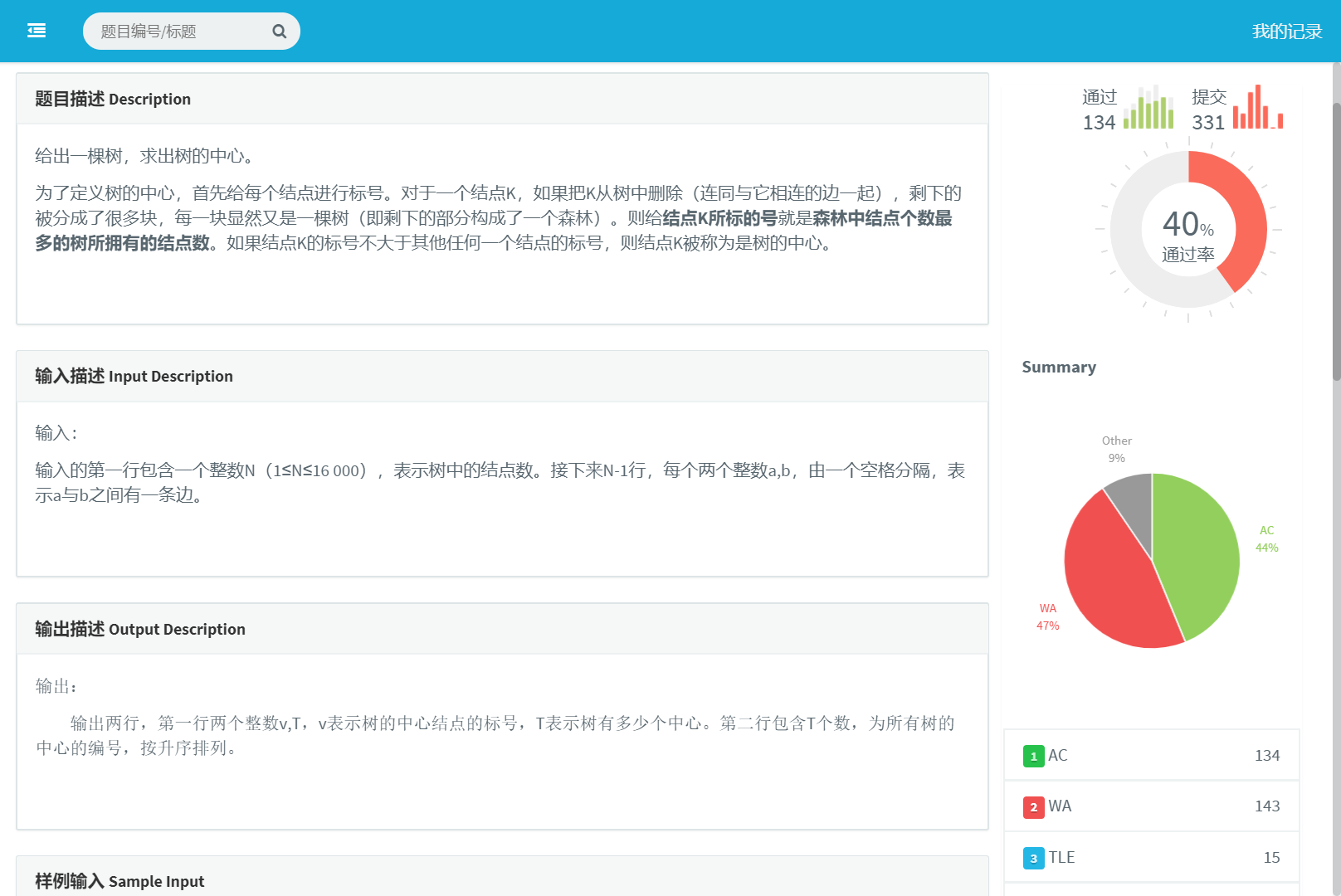
CODE[VS] 树的中心
【解题思路】
第一题是树的重心板题,我们只需要更新每一个节点下面子树的大小(包含自己)和下面每一棵子树的最大值,然后我们更新最小的最大值就可以了(还要算上自己爸爸的那棵子树的大小就用总节点个数减该节点子树的大小即可!),最后返回最小的最大值。(这道题还需要用一个priority_queue来维护最小的编号)
AC code:
/*
Name: CODEVS 3639 树的中心
Copyright: njc
Author: Mudrobot
Date: <DATETIME>
Description: Dynamic Programming
*/
#include<bits/stdc++.h>
#define gc() getchar()//caution!!!
#define N 16005
using namespace std;
/*inline char gc() {
static char buf[1<<18],*fs,*ft;
return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<18,stdin)),fs==ft)?EOF:*fs++;
}*/
template<class T>
inline void read(T &aa) {
register int k=0,f=1;
register char c=gc();
for (;!isdigit(c);c=gc()) if(c=='-')f=-1;
for (;isdigit(c);c=gc()) k=(k<<3)+(k<<1)+(c-'0');
aa=k*f;
}
template<class T>
inline void out(T x){if(x>9)out(x/10);putchar(x%10+'0');}
struct sd{int to,next;}edge[N*2];
struct sdp{int maxson,size;}node[N];
priority_queue<int, vector<int>,greater<int> > OMG;
int n,head[N],cnt,ans=-1;bool vis[N];
void add(int a,int b){
edge[++cnt].next=head[a];edge[cnt].to=b;head[a]=cnt;
}
void dfs(int u){
node[u].size=1;vis[u]=true;
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(!vis[v]){
dfs(v);
node[u].size+=node[v].size;
node[u].maxson=max(node[u].maxson,node[v].size);
}
}
node[u].maxson=max(node[u].maxson,n-node[u].size);
if(ans==-1||node[u].maxson<ans){
ans=node[u].maxson;
while(!OMG.empty())OMG.pop();
OMG.push(u);
}
else if(node[u].maxson==ans){
OMG.push(u);
}
}
int main()
{
read(n);int a,b;
for(int i=1;i<n;++i){
read(a);read(b);
add(a,b);add(b,a);
}
vis[1]=true;dfs(1);
int siz=OMG.size();
printf("%d ",ans);out(siz);putchar('
');
while(!OMG.empty()){
int now=OMG.top();OMG.pop();
out(now);putchar(' ');
}
return 0;
}
/*
7
1 2
2 3
2 4
1 5
5 6
6 7
*/
POJ 2631

这道题是一道非常典型的树上DP,我们记录对于每一个节点的最长路和次长路,然后最后把他们相加求最大即可。
AC code:
/*
Name: POJ 2631 Roads in the North
Copyright: njc
Author: Mudrobot
Date: 2018/10/18 17:06:57
Description: Dynamic Programming
*/
#include<cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#define gc() getchar()//caution!!!
#define N 10005
using namespace std;
/*inline char gc() {
static char buf[1<<18],*fs,*ft;
return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<18,stdin)),fs==ft)?EOF:*fs++;
}*/
template<class T>
inline void read(T &aa) {
register int k=0,f=1;
register char c=gc();
for (;!isdigit(c);c=gc()) if(c=='-')f=-1;
for (;isdigit(c);c=gc()) k=(k<<3)+(k<<1)+(c-'0');
aa=k*f;
}
template<class T>
inline void out(T x){if(x>9)out(x/10);putchar(x%10+'0');}
struct sd{
int to,next,val;
}edge[N*3];
bool vis[N];
int dis1[N],dis2[N],n,cnt,head[N],ans;
void add(int a,int b,int c){
edge[++cnt].next=head[a];edge[cnt].to=b;edge[cnt].val=c;head[a]=cnt;
}
void dfs(int fa,int u){
vis[u]=true;
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(!vis[v]){
dfs(u,v);
if(dis1[u]==0||dis1[u]<dis1[v]+edge[i].val){
dis2[u]=dis1[u];
dis1[u]=dis1[v]+edge[i].val;
}
else if(edge[i].val+dis1[v]>dis2[u])
dis2[u]=edge[i].val+dis1[v];
}
}
ans=max(ans,dis1[u]+dis2[u]);
}
int main()
{
//freopen(".in", "r", stdin);freopen(".out", "w", stdout);
int a,b,c;
while(scanf("%d%d%d",&a,&b,&c)==3){
add(a,b,c);add(b,a,c);n++;
}
dfs(1,1);
printf("%d",ans);
//fclose(stdin);fclose(stdout);
return 0;
}
/*
5 1 6
1 4 5
6 3 9
2 6 8
6 1 7
*/

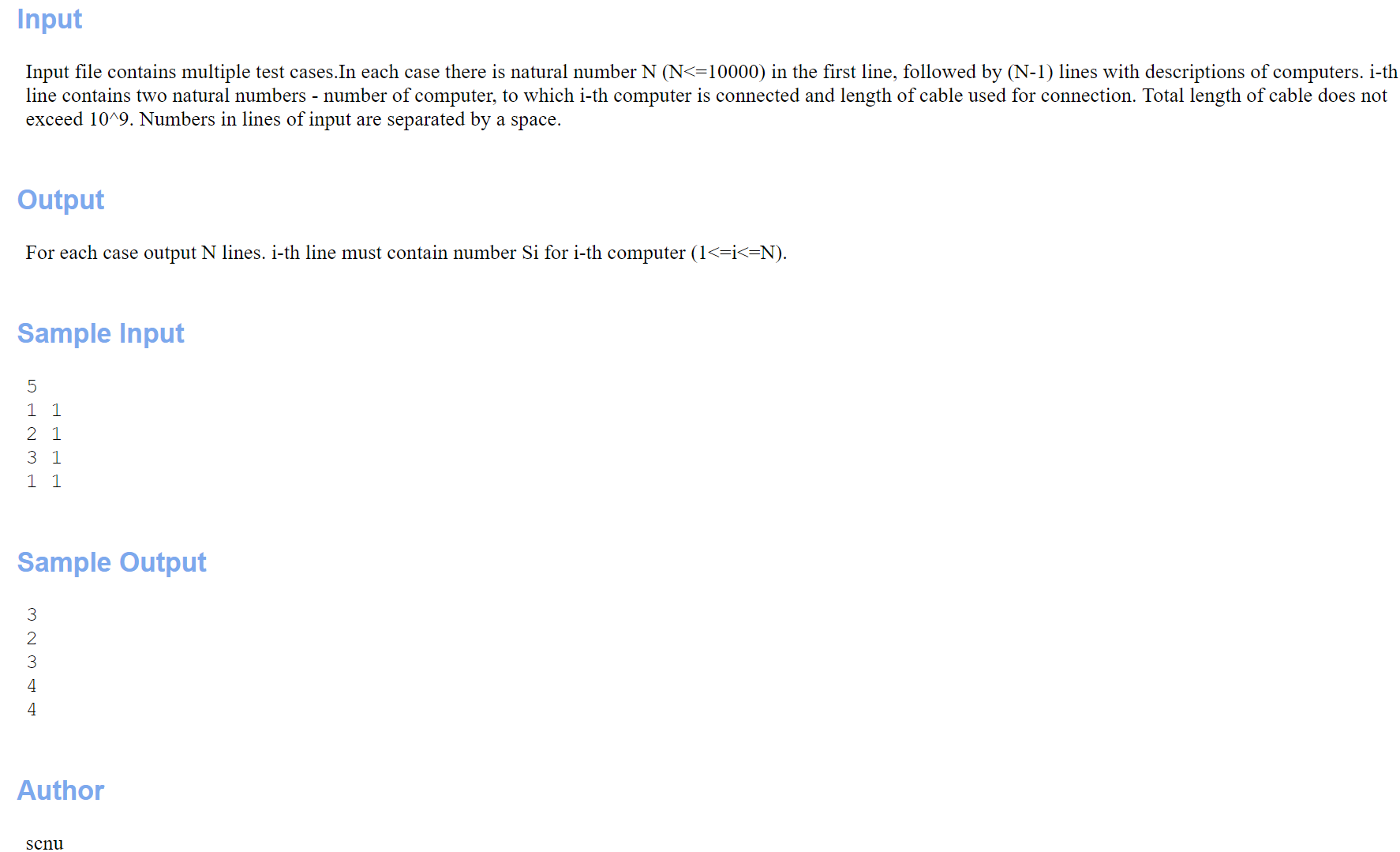
最后一道题就是求对于每一个点的最远距离!
有木有感觉这道题很像某凉心模拟D1T2,对其实这两道题是一样的,只是这道题稍微还要麻烦一些,那么题解大家可以看一下以前写的,这里就不在赘述了
AC code:
/*
Name: HDU 2196 Computer
Copyright: njc
Author: Mudrobot
Date: 2018/10/18 19:12:27
Description: Dynamic Programming
*/
#include<bits/stdc++.h>
#define gc() getchar()//caution!!!
#define N 10095
#define LL long long
using namespace std;
/*inline char gc() {
static char buf[1<<18],*fs,*ft;
return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<18,stdin)),fs==ft)?EOF:*fs++;
}*/
template<class T>
inline void read(T &aa) {
register LL k=0,f=1;
register char c=gc();
for (;!isdigit(c);c=gc()) if(c=='-')f=-1;
for (;isdigit(c);c=gc()) k=(k<<3)+(k<<1)+(c-'0');
aa=k*f;
}
template<class T>
inline void out(T x){if(x>9)out(x/10);putchar(x%10+'0');}
LL head[N],n,dis1[N],dis2[N],dis3[N],cnt,ans,suc[N];
bool vis[N];
struct sd{
LL to,next,val;
}edge[N*2];
void add(LL a,LL b,LL c){
edge[++cnt].next=head[a];edge[cnt].to=b;edge[cnt].val=c;head[a]=cnt;
}
void dfs(LL u){
vis[u]=true;
for(LL i=head[u];i;i=edge[i].next){
LL v=edge[i].to;
if(!vis[v]){
dfs(v);
if(dis1[u]<dis1[v]+edge[i].val){
dis2[u]=dis1[u];suc[u]=v;
dis1[u]=dis1[v]+edge[i].val;
}
else if(dis2[u]<dis1[v]+edge[i].val){
dis2[u]=dis1[v]+edge[i].val;
}
}
}
}
//void dfs2(LL u){
// vis[u]=true;
// for(LL i=head[u];i;i=edge[i].next){
// LL v=edge[i].to;
// if(!vis[v]){
// if(suc[u]==v){
// dis3[v]=max(dis3[u],dis2[u])+edge[i].val;
// }
// else dis3[v]=max(dis3[u],dis1[u])+edge[i].val;
// dfs2(v);
// }
// }
//}
void dfs2(LL fa,LL u,LL path){
vis[u]=true;
if(suc[fa]==u){
dis3[u]=max(dis3[fa],dis2[fa])+path;
}
else dis3[u]=max(dis3[fa],dis1[fa])+path;
for(LL i=head[u];i;i=edge[i].next){
LL v=edge[i].to;
if(!vis[v]){
dfs2(u,v,edge[i].val);
}
}
}
int main()
{
//freopen(".in", "r", stdin);freopen(".out", "w", stdout);
while(scanf("%d",&n)==1){
LL a,b;
memset(head,0,sizeof(head));
memset(dis1,0,sizeof(dis1));
memset(dis2,0,sizeof(dis2));
memset(dis3,0,sizeof(dis3));
memset(vis,false,sizeof(vis));
memset(suc,0,sizeof(suc));cnt=0;
for(LL i=2;i<=n;++i){
read(a);read(b);
add(i,a,b);add(a,i,b);
}
dfs(1);memset(vis,false,sizeof(vis));
dfs2(0,1,0);
for(LL i=1;i<=n;++i) out(max(dis1[i],dis3[i])),putchar('
');
}
//fclose(stdin);fclose(stdout);
return 0;
}
/*
5
1 1
2 1
3 1
1 1
*/
上面两个DFS都是对的!!!