ZOJ 3805--解题报告

题目相关:
　　3805相关链接: http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=5337
　　在二维的矩形上, 机器通过管道(pipe)连接(I型, L型),最终成为一个系统.
　　
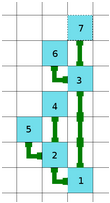
　　其规则大致提炼如下:
　　1). 编号大的输出可以成为编号小的输入(隐含拓扑序), 编号1只有输入/没有输出.
　　2). 每个节点最多有两个输入(弱化的图, 可以用二叉树来模拟)
　　3). 矩形世界没有高度限制, 但有宽度限制
　　目标就是:　
　　最能满足要求的最小宽度是多少?

思路解析：
　　本题隐含拓扑序(有向图), 同时每个节点最多两个子节点, 因此我们采用二叉树去模拟. 这种最优化问题, 有可能是动态规划(树形DP), 通过观察和琢磨. 可得出如下结论:
　　如果节点i存在子节点j, k, 若节点j的宽度==节点k的宽度, 则取子节点宽度+1, 若子节点不相同, 则取子节点最大宽度的.
　　转化为公式如下:

　　　　　　{	node(j) + 1; 　　　　　　　　if node(j) == node(k) 　　--(1)
node(i) = {	
　　　　　　{	max(node(j), node(k)); 　　if node(j) != node(k) 　　--(2)

　　其二叉树的是偏向树, 构建的时候, 往一个方向倾斜就是了.

AC代码:

#include <cstdio>

#include <vector>
#include <stack>

#include <functional>

struct tree_node_t {
        int left_index;
        int right_index;
        int value;
        tree_node_t(int li = -1, int ri = -1, int v = -1)
                : left_index(li), right_index(ri), value(v) {
        }
};

class machine {
public:
        machine() {
        }
	
	// *) 输入数据并构建二叉树
        void init_and_buildtree(int n, const std::vector<int> &datas) {
                arr_tree.resize(n);
                for ( int i = 1; i < datas.size(); i++ ) {
                        int idx = datas[i] - 1;
                        if ( arr_tree[idx].left_index == -1 ) {
                                arr_tree[idx].left_index = i;
                        } else {
                                arr_tree[idx].right_index = i;
                        }
                }
        }

	// *) 计算结果
	// *) 这边采用模拟堆栈的方式, 来实现递归调用, 因为节点有10000个. 
	// *）最差情况会导致二叉树成链表, 导致递归的调用栈达到10000
        int calculator() {

                std::stack<int> frames;
                frames.push(0);
                while ( !frames.empty() ) {
                        int idx = frames.top();

                        const int &li = arr_tree[idx].left_index;
                        const int &ri = arr_tree[idx].right_index;

                        if ( li != -1 && arr_tree[li].value == -1 ) {
                                frames.push(li);
                        } else if ( ri != -1 && arr_tree[ri].value == -1 ) {
                                frames.push(ri);
                        } else {
                                if ( li == -1 ) {
                                        arr_tree[idx].value = 1;
                                } else if ( li != -1 && ri == -1 ) {
                                        arr_tree[idx].value = arr_tree[li].value;
                                } else if ( li != -1 && ri != -1 ) {
                                        if ( arr_tree[li].value == arr_tree[ri].value ) {
                                                arr_tree[idx].value = arr_tree[li].value + 1;
                                        } else {
                                                arr_tree[idx].value = 
                                                        std::max(arr_tree[li].value, arr_tree[ri].value);
                                        } 
                                }
                                frames.pop();
                        }

                } 
                return arr_tree[0].value;
 
        }

public:
        std::vector<tree_node_t> arr_tree;
};

int main()
{

        int n;
        while ( scanf("%d", &n) != EOF ) {
                std::vector<int> datas(n, 0);
                for ( int i = 1; i < n; i++ ) {
                        scanf("%d", &datas[i]);
                }

                machine instance;
                instance.init_and_buildtree(n, datas);

                printf("%d
", instance.calculator());
        }
        return 0;

}

　　评注: 这边采用堆栈的方式来模拟递归调用, 是因为担心堆栈太深, 不过实际测试数据集, 没那么变态, 用递归的方式实现, 不仅优雅而且编码效率更高.

递归代码片段：

	// *)　递归函数, 划分子问题
int evaluate(int idx) {

　　int li = arr_tree[idx].left_index;
　　int ri = arr_tree[idx].right_index;
　　if ( li != -1 ) {
　　　　evaluate(li);
　　} 
　　if ( ri != -1 ) {
　　　　evaluate(ri);
　　} 

　　if ( li == -1 ) {
　　　　return arr_tree[idx].value = 1;
　　} else if ( li != -1 && ri == -1 ) {
　　　　return arr_tree[idx].value = arr_tree[li].value;
　　} else {
　　　　if ( arr_tree[li].value == arr_tree[ri].value ) {
　　　　　　arr_tree[idx].value = arr_tree[li].value + 1;
　　　　} else {
　　　　　　arr_tree[idx].value = std::max(arr_tree[li].value, arr_tree[ri].value);
　　　　}
　　}

　　return arr_tree[idx].value;

}
	
// *) 驱动函数
int calculator() {
　　return evaluate(0);
}