创建于:2019.5.23 - 5.25
个人思考过程,不是普遍运用的简便方法。
判断二叉树(不限于完全二叉树)一个结点的层数:
BinaryNode<T> p;
完全二叉树可以根据公式算出结点p的层数
假如结点p是第i个结点(i>=0),根据完全二叉树的性质h=(log2 i)+1可算出层数
假如要计算普通二叉树一个结点的层数,则没有公式,想算法:
- 思考:
- 利用层数遍历的得到的list
结果:只能得出每个结点的序号,无法判断其层数
- (行不通)方一:利用标明空子树的前序序列preList
定义一个int型 层数数组
逐个元素(包括空标识)往后遍历,每遍历一个层次+1,当上一个是空标识时,该元素层值,上两个是空标识时,层值 -1,上三个是空标识时,层值 -3
(可行)例一:
prelist= (A B D ^ G ^ ^ ^ C E ^ ^ F ^ ^)
level[]= 1 2 3 4 4 5 5 5 2 3 4 4 3 4 4

(不可行)例二:
Prelist= ( A B E ^ F ^ ^ C ^ D G ^ ^ ^ ^ )
Level[]= (1, 2 , 3, 4, 4 , 5, 5, 4, 5, 5, 6, 7 , 7, 7 ,4 )
3
- (已改进)方法二:利用 标明空子树标识的前序序列preList和层次遍历得到的levelList
*泛型用ArrayList代替数组
定义一个数组存放层次序号,长度为二叉树结点个数
主要遍历leveList,过程见例一
(可行)例一:
prelist= ( A B D ^ G ^^^C E ^^ F ^^)
levelList= (A B C D E F G )
level[]= 1 2 2 3 3 3 4

过程:
根结点只有一个,所以第一个A的层数肯定是1
第二个B的层数肯定是2;
LevelList下标指向C,preList下标指向D,若不相等,层数不变,且preList下标不变;
*为什么:
levelist中B的下一个是C,要么C是B的孩子,要么C是B的兄弟。在preList中,B的下一个元素不是C(C不是B的孩子),所以C肯定是B的兄弟
LevelList下标指向D,preList的下标仍是D,相等,层数+1(D的层数为3),preList下标+1(指向G)
*为什么:D在C的后面,D可能是B的孩子也可能是C的孩子,但是谁的孩子不重要,肯定不是兄弟(因为是二叉树),层数+1
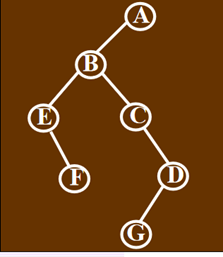
(可行)例二:
Prelist= ( A B E ^ F ^^ C ^ D G ^ ^^ ^)
levelList= (A B E C F D G )
level[]= ( 1, 2, 3, 3, 4, 4, 4 )

(改进后可行)例三:
Prelist= ( 100 , 40 , 19, ^^, 21,^^, 60, 28, 11, 5 , 2 ,^^, 3,^^,6, ^^,17, 7,^^,10,^^,32,^^)
levelList= (100, 40, 60, 19, 21, 28, 32, 11, 17 , 5, 6, 7, 10, 2, 3 )
level[]= ( 1, 2, 2, 3, 4, 4, 4, 4 , 4, 4, 4, 4, 4, 4, 4 )
3 3 3 4 4 5 5 5 5 6 6
改进1:(加条件)若prelist中遍历到的元素前有连续两个空标识,层数也不变(不论元素是否相等),preList下标+1
改进2:若在preList中遍历到levelList指向元素之前遍历过的元素,直接删除该元素
(不可以只是跳过,因为还要判断preFlag指向前两个元素是否为空标识^)
过程:
(部分)
LevelList中指标指向21,Prelist指向21,相等,但因为prelist的21前有两个连续空标识,所以层数不变;
*为什么:
LevelList中21在19的后面,21可能是19的孩子,21也可能是19的兄弟,看preList,虽然指向21,但前有两个空标识,说明21肯定不是19的孩子(两个孩子位被空标识占去),21只可能是19的兄弟,所以层数不变。
LevelList中指标指向28,Prelist指向60,因为levelList中60在28之前已经出现过,所以跳过这个元素,preflag++
*为什么:
判断一个元素的层数只需要知道,它与前面一个结点的关系(孩子还是兄弟),无需知道更前面哪些元素的信息。由于这个前面出现过的元素的层数已经计算得出,可以直接删去该元素。

例四:
preList= (18,7, ^^ , 11, 5, ^^, 6, 2,^^, 4,^^)
levelList= (18, 7, 11, 5, 6, 2, 4 )
Level[]= ( 1, 2, 2, 3, 3, 4, 4 )

算法实现代码:(已测试)
/** * @title: nodelevel * @description: get a given node's level * @author: Navis * @date: May 25, 2019 6:04:49 PM * @param p as root node * @return int :level * @throws:IllegalArgumentException:p==null */ public int nodelevel(BinaryNode<T> p) { if (this.root == null) return -1; if (p == null) throw new IllegalArgumentException("p==null"); int nodeCount = this.getNodeConut(); int[] lev = new int[nodeCount]; ArrayList preList = this.getPrelist(this.root); ArrayList levelList = this.levelList(); int nodeNum = levelList.indexOf(p.data); // p在levelList中的元素位置 lev[0] = 1;// 根结点只有一个,所以第一个元素层数是1 lev[1] = 2;// 第二个元素的层数是2; int preFlag = 2; Object firstBefore = preList.get(0); Object secondBefore = preList.get(1); // 计算层数数组lev[] for (int i = 2; i < levelList.size(); i++) {// 从第3个元素开始 for (int k = 0; k < i; k++) {// 若preFlag指向元素,在levelList的第i个元素前已经出现过,则删除该元素 if (preList.get(preFlag).equals(levelList.get(k))) { preList.remove(preFlag); k = 0;// k重新开始循环,判断更新后的preFlag位置元素是否之前出现过 } } if (firstBefore.equals("^") && secondBefore.equals("^")) { lev[i] = lev[i - 1]; preFlag++; while (preList.get(preFlag).equals("^")) { preFlag++; } firstBefore = preList.get(preFlag - 1);// preFlag指向元素的前面第一个元素 secondBefore = preList.get(preFlag - 2);// preFlag指向元素的前面第二个元素 } else { if (preList.get(preFlag).equals(levelList.get(i))) {// 相等 lev[i] = lev[i - 1] + 1; preFlag++; while (preList.get(preFlag).equals("^")) {// 跳过^空标识,指向有值元素 preFlag++; if (preFlag >= preList.size()) {// 防止preList后面全是^空标识,导致一直循环下去 break; } } firstBefore = preList.get(preFlag - 1); secondBefore = preList.get(preFlag - 2); } else {// 不相等 lev[i] = lev[i - 1]; } } // System.out.println(levelList.get(i) + ":" + lev[i]); } return lev[nodeNum]; } /** * @title: getNodeConut * @description: getNodeCount * @author: Navis * @date: May 24, 2019 10:55:13 AM * @return int nodeCount */ public int getNodeConut() { int nodeCount = 0; ArrayList prelist = this.getPrelist(this.root);// 得到带有空子树标识的prelist for (int i = 0; i < prelist.size(); i++) { if (prelist.get(i) != "^") nodeCount++; } return nodeCount; } /** * @title: getPrelist * @description: getPrelist; with emptySubTree sign * @author: Navis * @date: May 24, 2019 10:30:34 AM * @param BinaryNode<T> p * @return ArrayList prelist */ public ArrayList getPrelist(BinaryNode<T> p) { ArrayList prelist = new ArrayList(); preorder(prelist, p); return prelist; } /** * @title: preorder * @description: transverse a tree; preorder;get prelist with emptySubTree sign * @author: Navis * @date: May 23, 2019 8:55:17 AM * @param ArrayList prelist * @param BinaryNode<T> p */ public void preorder(ArrayList prelist, BinaryNode<T> p) { if (p != null) { prelist.add(p.data); preorder(prelist, p.left); preorder(prelist, p.right); } else prelist.add("^"); // 空子树标识 } /** * @title: levelList * @description: get levelList;levelOrder * @author: Navis * @date: May 24, 2019 11:54:07 AM * @return ArrayList levelList */ public ArrayList levelList() { LinkedQueue<BinaryNode<T>> queue = new LinkedQueue<>();// 空队列 BinaryNode<T> p = this.root;// 根结点不入队 ArrayList levelList = new ArrayList(); while (p != null) { levelList.add(p.data); // 将已出队结点p的元素值加入levelList if (p.left != null) queue.add(p.left);// p的左孩子入队 if (p.right != null) queue.add(p.right);// p的右孩子入队 p = queue.poll();// p指向出队结点,若队列为空返回null } return levelList; }