Uber Pool 是 Uber 类似于滴滴拼车的共享乘车产品。
拼车产品能够自动把路线重叠的乘客配对起来,这样对于所有乘客都能用更便宜的价格来享受乘车服务,路线重叠的越多,共享拼车就能提供越多的折扣。
怎样去设计一个好的拼车路线呢?Uber 设计了这样的指标,必须是便宜、快捷、方便和友好的。
从工程实现角度考虑,作为工程师我们怎样才能去测量一个拼车路线是否既快捷又高效呢?
怎样才能准确预测 2 个、3 个,或者 4 个乘客拼在一起会共同享受这个行程?
这些都是对于 Uber 拼车匹配系统的工程挑战。事实上 Uber 的拼车系统从最初上线到初步成型经过了 1 年半的迭代,更新了好几个版本。这些技术方案都很好地利用了图,可以说是技术人必读的工程案例。
项目动机
Uber 最初发布拼车服务是在 2014 年,但其实在很早 Uber 就已经对拼车这样的服务觊觎已久。
只不过一直没有辅助实行,是因为 Uber 想等到普通的打车服务的服务量达到一定规模,这样的话,从商业角度考虑才是进行更冒险创新的时机。
另外从工程角度考虑,原本的业务可以积累大量数据,为拼车这样的服务提供数据支撑。这是很值得我们技术人学习的思路。
不要一上来就 Over Engineering 过度技术复杂度。
明明 10 个用户都没有呢,就要考虑怎样应对 1 亿的流量,然后技术方案半年都做不出来。
正确的方式还是要跟着商业阶段来走,找到可以应对当前业务规模最简单的工程方案,同时也要往后看 3 年,但千万不要看得太多,否则很容易因为工程技术资源不够,反而影响了业务迭代速度。
话又回到 2014 年。在正式上马拼车业务之前,Uber 先进行了技术模拟,类似于股票交易的回溯测试,先利用已经积累的历史打车业务数据,来模拟演算拼车业务的可行性。
结果是令人兴奋的,他们发现在旧金山,有超过 80% 的行程是和别的行程有很大重叠的。
这是一个令人震惊的数字,因为要知道 Uber 当时在路上的车辆仅仅是旧金山路上车辆很小的一部分,即使如此,已经能有相当多的行程可以被匹配了。
所以他们清楚地看到了这里面的商业潜力及社会价值。这样既可以让司机开同样的车赚更多的钱,又可以减少路上的车辆保护环境。
技术方案选择
在最开始的拼车方案设计中,根据乘客输入的起始点,会收到一个固定的报价,然后 Uber 拼车服务会让乘客等待 1 分钟,来匹配其他的乘客和司机,如果 1 分钟后没有找到匹配合适的同行乘客,Uber 仍然会按照报价的金额派出单独的司机来进行接送。在尝试了这个固定 1 分钟的方案之后,Uber 发现这个方案还是有很多问题。
他们又尝试了动态窗口式的匹配系统,也就是说不是所有的乘客都等待固定的 1 分钟,而是把乘客放在一个动态的匹配窗口,比如 10 分钟的匹配窗口,那么 8:03 和 8:09 开始叫车的乘客都会待在 8:00 ~ 8:10这样的一个窗口里等待匹配。很显然,匹配窗口越大,系统能找到匹配的几率就越高,但窗口也不是固定大小的,比如对于人口密度比较低的美国中部城市,窗口可以设到 15 分钟;但对于人口集中的大城市,或者是上下班高峰时,窗口只需要 30 秒就能找到匹配同行的乘客了。因此,窗口时间短,用户体验也会更好,因为用户就不需要等待很长时间了,但是这样的方案还是有一些缺点。
在同一个时间窗口里找到足够的司机变得很难。因为 Uber 的系统必须要在 10 分钟窗口结束时找到拼车司机,不然就要为每一个乘客单独派送专车司机且按照拼车的价格承诺,也就是对系统造成了成本压力。10 分钟的窗口对用户来讲也有点长了,最终上线的 Uber 拼车服务等待时间为 1 分钟。
简单的匹配算法
Uber 在 2014 年的时候业务发展非常快,当时强调的工程文化是敏捷迭代。
正如我之前所说他们追求先快速上线最简单的匹配系统,这其实是一个基于贪心算法思想的匹配系统。
贪心算法的基本理念就是找到局部最优,而暂不考虑全局最优。
在拼车匹配系统里,一个贪心的匹配就是先快速找到第一个符合条件的拼车配对组合,而不考虑是否是这个时间窗口里最好的匹配。
在产品上线的最初阶段,事实上贪心算法是非常合适的,因为用户规模不大,往往一个时间窗口内可供选择的乘客也不多。
如果非要追求全局最优则需要花费大量的时间,并且这个最初上线的系统利用起始点的直线距离以及平局车速来快速估算预计时间。
这个最初的系统会便利所有的两两乘客,也就是 O(n^2) 的时间复杂度,这里面的 n 是多少呢?
让我们来把乘客的起始点标注比如乘客 A 的起始点分别为 A 和 A’,B 的起始点就是 B 和 B’。
若要匹配 A 和 B 两个乘客的话,则有 24 种可能的匹配!比如 ABB’A’、ABA’B’、B’A’BA、B’AA’B、B’ABA’、BAA’B’、AA’B’B、B’BAA’ 等。
如果你学过排列组合的话,就知道这个是 4*3*2*1 种可能性,但实际上合理的组合只有 4 种,因为 A’ 终点不可能出现在 A 起点之前,同时,AA’BB’ 这样的组合也不存在,因为这样路线就没有重叠了。
所以对于一个有 n 个乘客的系统来说,我们需要遍历 4*n^2 种可能,然后再来寻找最优的组合。这样的暴力搜索法用伪代码来实现是这样子的:
def make_matches(all_rides): for r1 in all_rides: for r2 in all_rides: orderings = [] for ordering in get_permutations(r1, r2): if is_good_match(r1, r2, ordering): orderings.append(ordering) best_ordering = get_best_ordering(r1, r2, orderings) if best_ordering: make_match(r1, r2, best_ordering) // etc ...
在搜索过程中也要考虑一些筛选条件,比如绕路和接客时间。
一个合理的拼车组合,必须要保证对于每一个乘客来说,拼车之后的绕路要在一个可接受的范围以内。比如说我本来只是一个 10 分钟的行程,如果因为拼车绕了 20 小时的路肯定是非常糟糕的用户体验;相反如果我本来就是 2 个小时的路程,绕路 20 分钟可能还可以接受,还好绕路其实是很容易计算的。
我们可以先计算乘客直接到达目的地的时间,再计算拼车之后到达目的地的时间,这两个时间差值就是绕路时间。
对于一个 A → B → A’ → B’ 的组合,A 的绕路是 A 到 B 再到 A’ 的行程,减去 A 到 A’ 的行程,相似的也要计算乘客额外的等待接驾时间。还是对于 A→ B→ A’→ B’ 这样一个行程来说,A 的等待时间是司机→ A 的时间,B 的等待时间是司机→ A → B 的时间。一般来说第二个乘客的接驾时间更长,但是绕路时间更短。
在这个简单匹配算法后,Uber 开始改进匹配系统。Uber 收到了很多用户的反馈,因为使用了拼车,必须先要坐到很远的地方再掉头回来,觉得这个系统很不智能。
Uber 意识到乘客不愿意走回头路,也就是说整个行程的方向要和本来的方向符合。
这也促使了 Uber 改进了第二代和第三代拼车匹配系统。
第三代拼车匹配系统
等迭代到第三代拼车匹配系统时,Uber 的工程师已经认识到了再不使用图这个武器,已经无法完成业务需要了,这也正是告诉我们学好数据结构的重要性。
没有数据结构的深厚功力,很容易无法承担业务的重大挑战。
Uber 发现不能再继续使用贪心算法了,而是使用权重图的重要算法:最大匹配算法。
这个算法同时要能够预测短期内的拼车需求,作出一个全局最优的匹配决定。

如图中所示,如果我们用图来建模拼车系统的话,则可以把乘客的起点和终点都看作是图中的节点,这个图中边的权重可以被认为是开车的时间。
一个最优的拼车订单,是找到一个连接至少 2 个乘客的起点和终点的几条边,并且这几条边的组合权重之和相比乘客的数量是图中最小的。
这是一个经典的 NP 难题,只能用 n 的多项式时间来完成。
Uber 的工程师在原先的贪心算法上加了一个改进的方案,称为路线切换。
其实路线切换很简单,可以说是一个讨巧的办法。它是利用上面的贪心算法找到局部最优,然后再利用司机去接驾的时间继续为乘客匹配拼车路线,一旦找到更优的匹配就把司机切换了。利用这样的时间差,Uber 把搜索最优匹配的时间从几十秒变成了几分钟。下图就是一个路线切换的示意图。
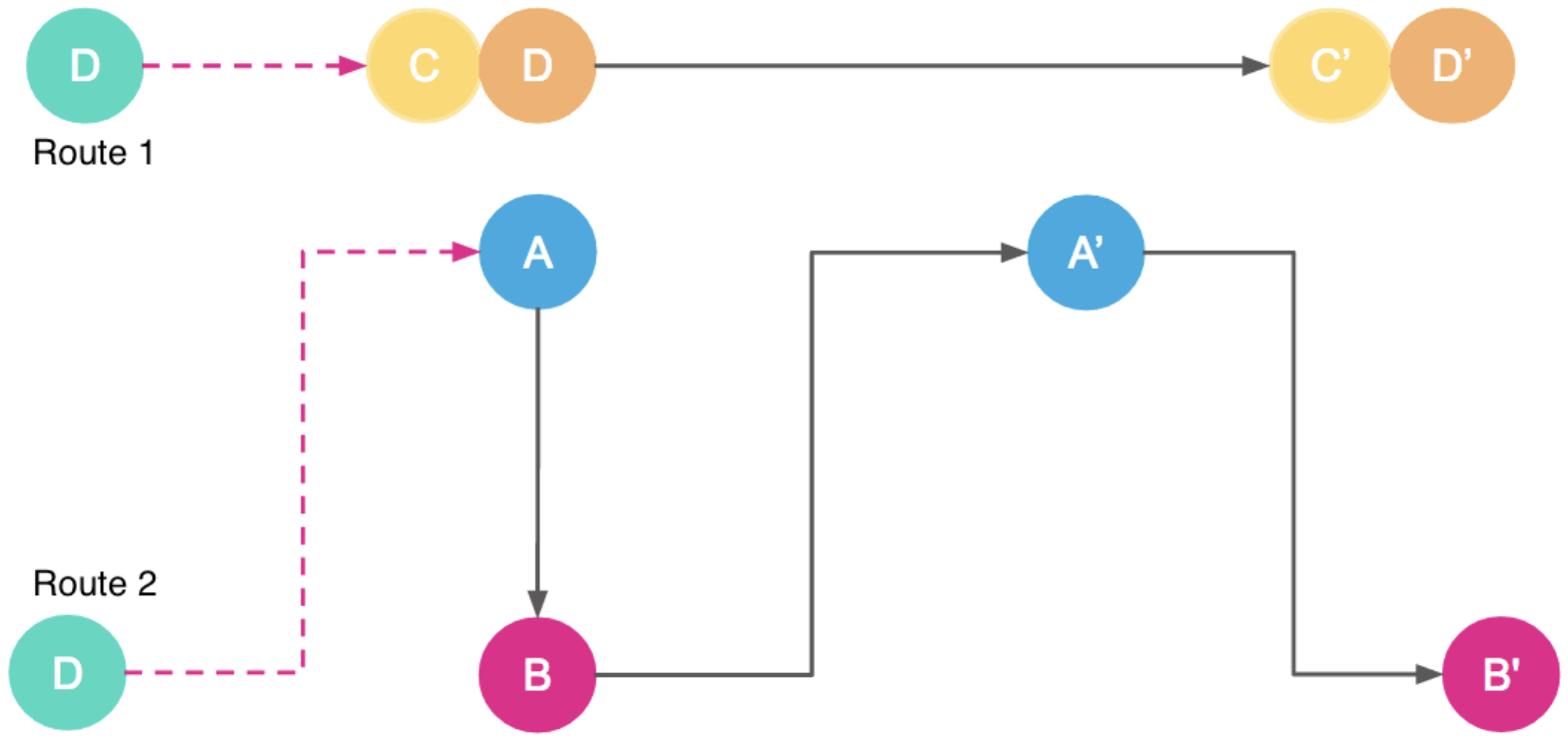
除了路线切换之外,在第三代拼车匹配系统中,Uber 工程师们还改进了称为滚雪球式匹配算法。
它的意思是一旦通过前面的贪心算法,和路线切换确定了一条拼车路线以后,系统会利用这条路线去不断尝试接受新的拼车乘客,也就是说有可能在行程中不断有新的乘客被加入到这个拼车线路中。
通过这些改进,Uber 工程师很好的去逼近 NP 难题的全局最优,并且这个全局最优在现实中很难解决,因为无法预测未来的乘车需求。
Uber 的方案很好地利用了时间差,非常有效率的在拼车线路的不同阶段去尝试找到局部最优匹配。
总结
这一课时我们分析了 Uber 的拼车系统案例,它属于图的最大匹配问题,可以看到 Uber 是怎样一步一步迭代技术方案,并最终逼近最优解的过程,同时对于我们技术团队的方案设计也很有启发。
在早期业务比较小时千万不要过度优化,而是要用最简单的方案快速验证,收集更多用户和数据来不断改进系统。