1 定义
队列是只允许在一端进行插入操作,另一端进行删除操作的线性表。
队列是一种先进先出(FIST IN FIRST OUT)的线性表,简称FIFO。允许插入的一端称为队尾,允许删除的一端称为对头。
2 队列的顺序存储结构
(1)队列顺序存储的不足--引出循环队列
假设一个队列有n个元素,则顺序存储的队列需要建立一个大于n的数组,并把队列的所有元素存储在数组的前n个单元,数组下标为0的一端即为对头。
所谓的入队,就是在队尾追加一个元素,不需要移动任何元素,所以时间复杂度为O(1).
队列的出队是在对头,即下标为0的位置,也就意味着,队列中的所有位置都得向前移动,以保证下标为0的位置,即对头不为空。此时时间复杂度为O(n)。
可是有时候想想,为什么出队列时一定要全部移动呢?如果不限制队列的元素一定要存储在数组的前n个单元,出队的性能就会大大增加。也就是说,队头不需要一定在下标为0的位置。

为了避免当只有一个元素时,对头和队尾重合使得处理变得麻烦,所以引入两个指针,front指针指向对头元素,rear指针指向队尾元素的下一个元素。这样当front等于rear时,不是队列中有一个元素,而是表示空队列。
假设数组的长度为5,空队列及初始状态如左图所示,front与rear指针都指向下标为0的位置。当队列中有4个元素时,front指针不变,rear指针指向下标为4的位置。
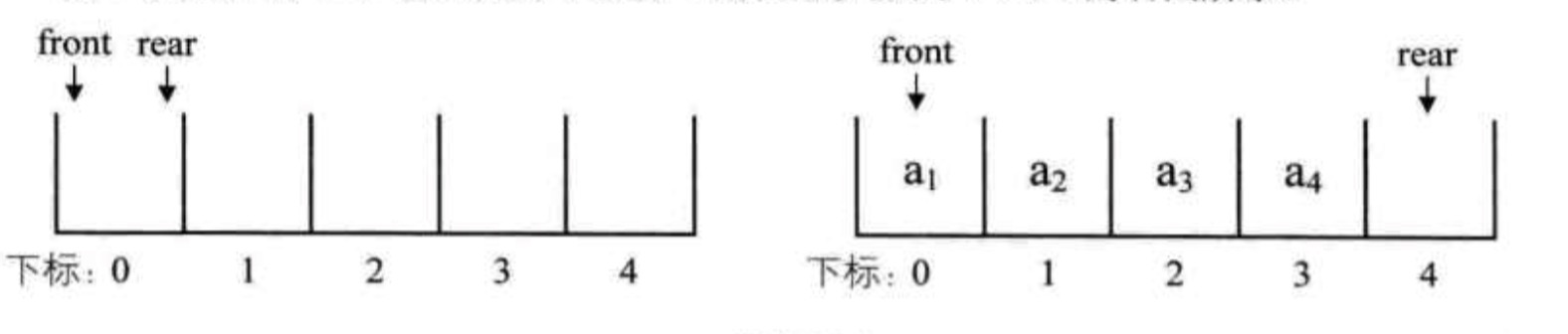
此时出队两个元素,则front指针指向下标为2的位置,rear不变。再入队一个元素,front指针不变,此时rear指针移动到数组之外。
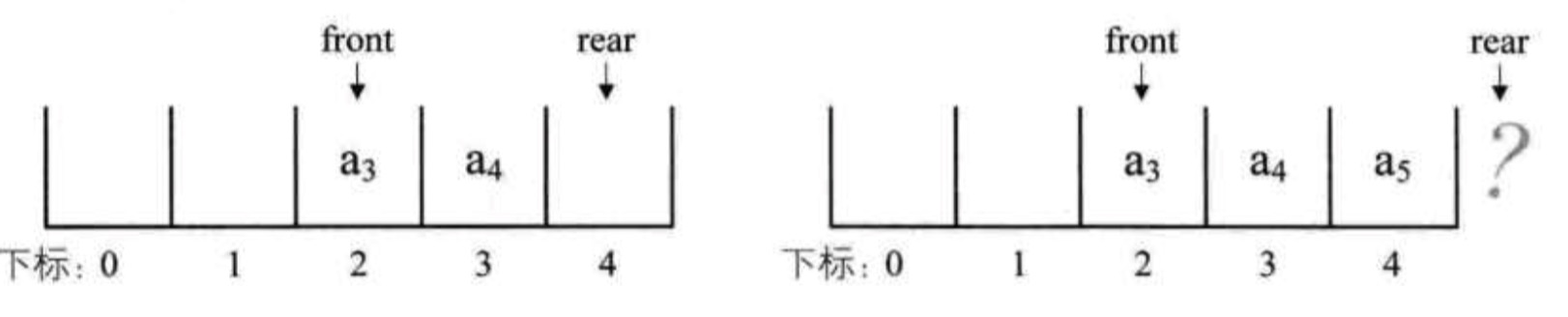
假设这个队列中的总个数不超过5个,但目前如果接着入队的话,会导致数组越界的错误,但是队列在下标为0和1的位置是没有元素的。我们把这种现象叫做“假溢出”。
为了解决“假溢出”的问题,我们引入循环队列。
(2)循环队列
为了解决“假溢出”的办法,就是队后面满了,再从头开始,也就是头尾相接的循环。我们把队列的这种投喂相接的顺序存储结构称为循环队列。
继续刚才的例子,将rear指针指向下标为0的位置,就不会导致rear指针指向不明的问题。
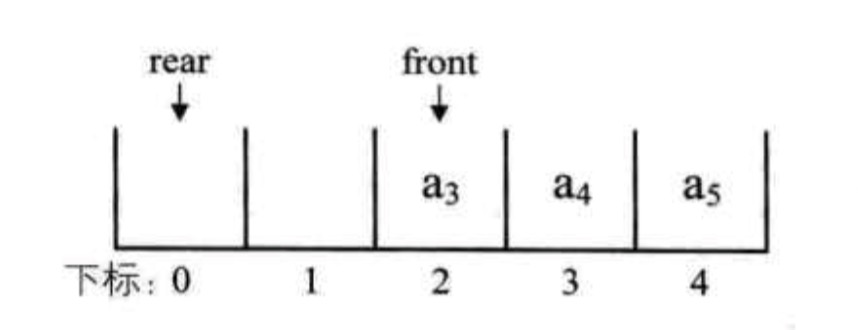
接着入队两个元素,会发现rear指针与front重合了。

此时问题又来了,刚才说了,当rear等于front时,表示是空队列,现在当队列满时,rear也等于front。那么如何判断队列到底是空的还是满的了?
解决办法为:当队列空时,判断条件就是rear=front, 当队列满时,我们修改其判断条件,保留一个元素空闲。也就是说,队列满时,数组中还有一个空闲单元。以下两种情况,我们都认为队列已经满了。

由于rear可能比front大,也可能比front小,所以假设队列的最大尺寸为QueueSize, 队列满的判断条件改为(rear + 1)%QueueSize = front. 队列的长度为(rear - front + QueueSize)% QueueSize.
循环队列的顺序存储结构为
typedef int QElemType; typedef struct { QElemType data[MAXSIZE]; int rear; //头指针 int front; //尾指针,若队列不为空,指向队尾元素的下一个元素 }SqQueue;
循环队列的初始化
//初始化一个空队列 Status InitQueue(SqQueue *Q) { Q->rear = 0; Q->front = 0; return OK; }
循环队列求当前队列的长度
//返回Q的元素个数,也就是队列的当前长度 int QueueLength(SqQueue Q) { return (Q.rear - Q.front + MAXSIZE) % MAXSIZE; }
循环队列的入队操作
//若队列未满,插入元素e为新的队尾元素 Status insertQueue(SqQueue *Q, QElemType e) { if ((Q->rear + 1) % MAXSIZE == Q->front) { //队满 return ERROR; } Q->data[Q->rear] = e; Q->rear = (Q->rear + 1) % MAXSIZE; return OK; }
循环队列的出队操作
//若队列不为空,删除Q的对头元素,并用e返回 Status deleteQueue(SqQueue *Q, QElemType *e) { if (Q->rear == Q->front) { //队空 return ERROR; } *e = Q->data[Q->front]; Q->front = (Q->front + 1) % MAXSIZE return OK; }