The Meeting Place Cannot Be Changed

题面：

The main road in Bytecity is a straight line from south to north. Conveniently, there are coordinates measured in meters from the southernmost building in north direction.

At some points on the road there are n friends, and i-th of them is standing at the point xi meters and can move with any speed no greater than vi meters per second in any of the two directions along the road: south or north.

You are to compute the minimum time needed to gather all the n friends at some point on the road. Note that the point they meet at doesn't need to have integer coordinate.

Input

The first line contains single integer n (2 ≤ n ≤ 60 000) — the number of friends.

The second line contains n integers x1, x2, ..., xn (1 ≤ xi ≤ 109) — the current coordinates of the friends, in meters.

The third line contains n integers v1, v2, ..., vn (1 ≤ vi ≤ 109) — the maximum speeds of the friends, in meters per second.

Output

Print the minimum time (in seconds) needed for all the n friends to meet at some point on the road.

Your answer will be considered correct, if its absolute or relative error isn't greater than 10 - 6. Formally, let your answer be a, while jury's answer be b. Your answer will be considered correct if 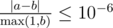 holds.

很容易就可以联想到可以用二分来解决，这里选择二分时间来枚举区间，check函数判断对于每一个时间是否可以保证所有人能到达得一个区间，只要存在一个人无法到达左后得小区间就返回false

但是写代码得过程中遇到一些精度问题，自己得二分和chenk函数应该都是没问题，但是怎么都过不了样例。后来东巨发现我写的double类型判断大小的函数函数应该加上精度考虑，就对了。xwdtql！

贴代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

#define eps 1e-7
#define INF 1e18
#define maxn 60005

int n;

double xi[maxn],sp[maxn];

double Max(double a, double b) {
    return (a - b  > eps) ? a : b ; //这里如果写成 a - b > 0 ? a : b 就不行
}
double Min(double a, double b) {
    return (a - b > eps) ? b : a;
}

bool check(double t) {
    double lp = xi[1] - sp[1] * t, rp = xi[1] + sp[1] * t;
    for (int i = 1; i <= n; ++i) {
        double a, b;
        a = xi[i] - sp[i] * t;
        b = xi[i] + sp[i] * t;
        lp = Max(lp, a);
        rp = Min(rp, b);
    }
    if (lp <= rp) return true;
    return false;
}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%lf",&xi[i]);
    for(int i=1;i<=n;i++) scanf("%lf",&sp[i]);
    double l=0,r=1e9,ans;
    while(l<=r)
    {
        double mid=(l+r)/2.0;
        if(check(mid)) r=mid-eps,ans=mid;
        else l=mid+eps;
    }
    printf("%.7lf",ans);
    return 0;
}