[题解][SHOI2013]超级跳马 动态规划/递推式/矩阵快速幂优化

这道题... 让我见识了纪中的强大

这道题是来纪中第二天(7.2)做的,这么晚写题解是因为

我去学矩阵乘法啦啦啦啦啦
对矩阵乘法一窍不通的童鞋戳链接啦

层层递推会TLE,正解矩阵快速幂

首先题意就是给你一个 n 行m 列 的格子图 一只马从棋盘的左上角跳到右下角。每一步它向右跳奇数列，且跳到本行或相邻行。

题意很简单
暴力dp的思路也很简单
但是数据很恶心
虽然远古一点,但毕竟是省选题

1 ≤ n ≤ 50，2 ≤ m ≤ 10^9

不过还是给了我们一点提示:
n这么小?

总之我们先找出转移式
对于每一个点 (i,j) 的
我们可以从它左边所有奇数行跳过来
所以DP[i][i]=sum( 左边间隔偶数列上中下三行的和 )
如果每个点都往前找一次的话
这样复杂度是O(n²m)
得分10

所以我们想到了前缀和
别问我怎么想到的,有什么套路
这种东西真的是灵感

DP[i][j]保存 (i-1)列+(i-3)列......上中下三行的和
这么简化之后,我们的递推式就好写了
时间复杂度O(mn)
甚至可以用滚动数组优化
这样空间也不是问题了O(n)
得分50

DP[i][j] = DP[i-2][j] + DP[i-1][j+1] + DP[i-1][j] + DP[i-1][j-1]

那么怎么得满分呐?
敲黑板划重点啦

观察一下递推式......嗯?递推式啊
那就用矩阵快速幂吧
不过这道题的递推关系有点复杂啊___二维递推

越到这种时候越要冷静观察,感性思考

再吱一声:不会矩阵快速幂的同学戳链接呐

观察一下,递推式需要两行数据
我们把这两行看成两个数据
跟斐波那契数列的递推矩阵一样放在一行

展开来就是像这样的东西(以n=4为例)

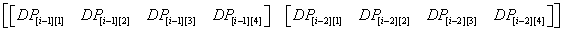
再展开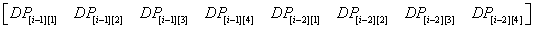

虽然这么看很乱(个P),不过我们只要仔细思考其中的意义就不难明白了

 这样写下来之后,我们所需要的 DP[i-2][j] , DP[i-1][j+1] , DP[i-1][j] , DP[i-1][j-1]
就都出现在矩阵L中了

开始填矩阵R

根据矩阵乘法左行右列的规则,每次乘法 矩阵L 的每个元素都有机会被乘到
我们可以在填矩阵的时候自己选择系数(多方便啊)

由于我们的矩阵是 2n 的 , 所以我们需要一个2n*2n的正方形矩阵(我都以4为例呐)

(这是一个已经填好的矩阵)

答案A 的第一行 第一列 等于 矩阵L的第一行 * 矩阵R的第一列(详见矩阵乘法详解)
由于系数都是1,所以我们填1

我还是随便解释一个吧
不然跟其他的题解有什么区别

DP[i][3] = DP[i-2][3] + DP[i-1][2] + DP[i-1][3] + DP[i-1][4]

所以在这个矩阵中,第3列是这么乘的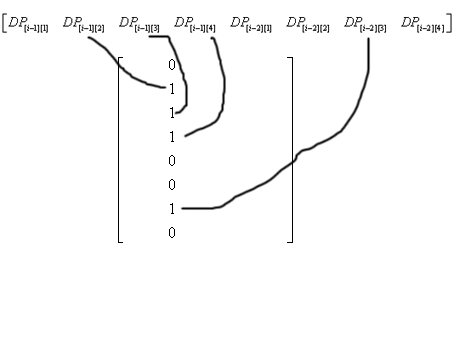

大家一定都懂了

对吧....

虽然n是不同的,但是矩阵的构造是相似的
所以我写了一个函数来初始化数组L和R

void _make(int A[LEN][LEN], int B[LEN][LEN], int len) {
    for (int i = 1; i <= len; ++i) {
        for (int j = 1; j <= len; ++j) {
            if (i == j)
                A[i][j] = A[len + i][j] = A[i][len + j] = 1;
            if (i - j == 1 || j - i == 1)
                A[i][j] = 1;
        }
    }
    B[1][1] = B[1][2] = B[1][len + 1] = 1;
}

 然后矩阵快速幂就完事了（详细过程见淼淼的矩阵快速幂详解

来了源码

// 2

#include <iostream>
using namespace std;


#define LEN 100
#define MOD 30011

unsigned int n, m;

int mat[LEN][LEN] = {0}, ans[LEN][LEN];

void _make(int A[LEN][LEN], int B[LEN][LEN], int len);
void _mul(int L[LEN][LEN], int R[LEN][LEN], int A[LEN][LEN], int x, int y, int z);
void _mi(int L[LEN][LEN], int R[LEN][LEN], int A[LEN][LEN], int x, int y, int m);

int main() {
    freopen("2.in", "r", stdin);
    cin >> n >> m;
    if (m == 1) {
        cout << ((n == 1) ? (1) : (0));
        return 0;
    }
    _make(mat, ans, n);
    _mi(ans, mat, ans, 1, 2 * n, m - 3);
    cout << (ans[1][n - 1] + ans[1][n]) % MOD;
    return 0;
}

void _make(int A[LEN][LEN], int B[LEN][LEN], int len) {
    for (int i = 1; i <= len; ++i) {
        for (int j = 1; j <= len; ++j) {
            if (i == j)
                A[i][j] = A[len + i][j] = A[i][len + j] = 1;
            if (i - j == 1 || j - i == 1)
                A[i][j] = 1;
        }
    }
    B[1][1] = B[1][2] = B[1][len + 1] = 1;
}

void _mul(int L[LEN][LEN], int R[LEN][LEN], int A[LEN][LEN], int x, int y, int z) {
    long long cmp[LEN][LEN] = {0};
    for (int i = 1; i <= x; ++i)
        for (int j = 1; j <= z; j++)
            for (int k = 1; k <= y; k++)
                cmp[i][j] = (cmp[i][j] + L[i][k] * R[k][j]) % MOD;
    for (int i = 1; i <= x; ++i)
        for (int j = 1; j <= z; ++j)
            A[i][j] = cmp[i][j];
}

void _mi(int L[LEN][LEN], int R[LEN][LEN], int A[LEN][LEN], int x, int y, int m) {
    int cmp[LEN][LEN];
    for (int i = 1; i <= x; ++i)
        for (int j = 1; j <= y; ++j)
            cmp[i][j] = L[i][j];
    while (m > 0) {
        if (m & 1)
            _mul(cmp, R, cmp, x, y, y);
        m >>= 1;
        _mul(R, R, R, y, y, y);
    }
    for (int i = 1; i <= x; ++i)
        for (int j = 1; j <= y; ++j)
            A[i][j] = cmp[i][j];
}